针孔相机、鱼眼相机模型推导
针孔相机、鱼眼相机模型
一、针孔相机模型
空间的三维物体要成像到相机的 CMOS/CCD 上面,形成了图像。图像上的每个点对应空间上的一个点。
将世界坐标系上的一点 (x,y,z)映射到CMOS/CCD图像坐标系上,只要两步:
- 世界坐标系的坐标转化到相机坐标系。
- 相机坐标系坐标转化到图像坐标系。
1.1 世界坐标系到相机坐标系
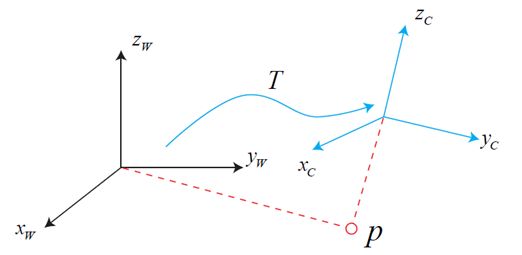
即要将世界坐标系上的点 ( X w , Y w , Z w ) T (X_w,Y_w,Z_w)^T (Xw,Yw,Zw)T 转化成相机坐标系上的点 ( X c , Y c , Z c ) T (X_c,Y_c,Z_c)^T (Xc,Yc,Zc)T。
根据线性代数(计算机图形学)的知识可以知道,坐标系的转化只需要将原坐标乘以一个旋转矩阵再加上一个平移矩阵即可。公式如下:
[ X c Y c Z c ] = [ R 11 R 12 R 13 R 21 R 22 R 23 R 31 R 32 R 33 ] [ X w Y w Z w ] + [ t 1 t 2 t 3 ] \left[ \begin{array}{l}{X_{c}} \\ {Y_{c}} \\ {Z_{c}}\end{array}\right]=\left[ \begin{array}{lll}{R_{11}} & {R_{12}} & {R_{13}} \\ {R_{21}} & {R_{22}} & {R_{23}} \\ {R_{31}} & {R_{32}} & {R_{33}}\end{array}\right] \left[ \begin{array}{l}{X_{w}} \\ {Y_{w}} \\ {Z_{w}}\end{array}\right]+\left[ \begin{array}{c}{t_{1}} \\ {t_{2}} \\ {t_{3}}\end{array}\right] ⎣⎡XcYcZc⎦⎤=⎣⎡R11R21R31R12R22R32R13R23R33⎦⎤⎣⎡XwYwZw⎦⎤+⎣⎡t1t2t3⎦⎤
写成齐次矩阵的形式如下:
[ X c Y c Z c 1 ] = [ R 11 R 12 R 13 t 1 R 21 R 22 R 23 t 2 R 31 R 32 R 33 t 3 0 0 0 1 ] [ X w Y w Z w 1 ] \left[ \begin{array}{c}{X_{c}} \\ {Y_{c}} \\ {Z_{c}} \\ {1}\end{array}\right]=\left[ \begin{array}{cccc}{R_{11}} & {R_{12}} & {R_{13}} & {t_{1}} \\ {R_{21}} & {R_{22}} & {R_{23}} & {t_{2}} \\ {R_{31}} & {R_{32}} & {R_{33}} & {t_{3}} \\ {0} & {0} & {0} & {1}\end{array}\right] \left[ \begin{array}{c}{X_{w}} \\ {Y_{w}} \\ {Z_{w}} \\ {1}\end{array}\right] ⎣⎢⎢⎡XcYcZc1⎦⎥⎥⎤=⎣⎢⎢⎡R11R21R310R12R22R320R13R23R330t1t2t31⎦⎥⎥⎤⎣⎢⎢⎡XwYwZw1⎦⎥⎥⎤
平移矩阵有三个参数,分别是相机坐标系x,y,z轴相对于世界坐标系的位移
旋转矩阵也有三个参数,分别是相机坐标系x,y,z轴相对于世界坐标系的旋转角度
其中,旋转矩阵的具体形式如下:
[ cos ( β ) cos ( θ ) cos ( β ) sin ( θ ) − sin ( β ) − cos ( α ) sin ( θ ) + sin ( α ) sin ( β ) cos ( θ ) cos ( α ) cos ( θ ) + sin ( α ) sin ( β ) sin ( θ ) sin ( α ) cos ( β ) sin ( α ) sin ( θ ) + cos ( α ) sin ( β ) cos ( θ ) − sin ( α ) cos ( θ ) + cos ( α ) sin ( β ) sin ( θ ) cos ( β ) ] \left[ \begin{array}{ccc}{\cos (\beta) \cos (\theta)} & {\cos (\beta) \sin (\theta)} & {-\sin (\beta)} \\ {-\cos (\alpha) \sin (\theta)+\sin (\alpha) \sin (\beta) \cos (\theta)} & {\cos (\alpha) \cos (\theta)+\sin (\alpha) \sin (\beta) \sin (\theta)} & {\sin (\alpha) \cos (\beta)} \\ {\sin (\alpha) \sin (\theta)+\cos (\alpha) \sin (\beta) \cos (\theta)} & {-\sin (\alpha) \cos (\theta)+\cos (\alpha) \sin (\beta) \sin (\theta)} & {\cos (\beta)}\end{array}\right] ⎣⎡cos(β)cos(θ)−cos(α)sin(θ)+sin(α)sin(β)cos(θ)sin(α)sin(θ)+cos(α)sin(β)cos(θ)cos(β)sin(θ)cos(α)cos(θ)+sin(α)sin(β)sin(θ)−sin(α)cos(θ)+cos(α)sin(β)sin(θ)−sin(β)sin(α)cos(β)cos(β)⎦⎤
α \alpha α:x轴的旋转量. β \beta β:y轴的旋转量. θ \theta θ:z轴的旋转量
相机的外参就是旋转矩阵的三个参数加上平移矩阵的三个参数。代表了相机相对于世界坐标系的位姿
1.2 相机坐标系坐标转化到图像坐标系
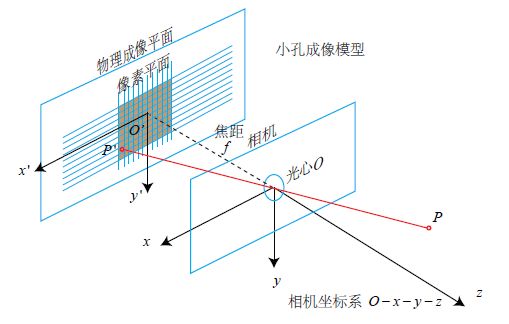
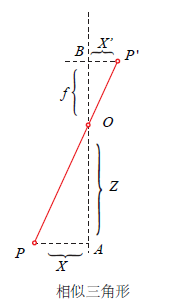
相机坐标系上的点 ( X , Y , Z ) T (X,Y,Z)^T (X,Y,Z)T 转化成图像坐标系上将会变成
( f X Z , f Y Z ) T \left(\frac{f X}{Z}, \frac{f Y}{Z}\right)^{T} (ZfX,ZfY)T
用齐次坐标表示相当于 ( X , Y , Z , 1 ) T → ( f X , f Y , Z ) T (\mathrm{X}, \mathrm{Y}, \mathrm{Z}, 1)^{T} \rightarrow(f X, f Y, Z)^{T} (X,Y,Z,1)T→(fX,fY,Z)T
用矩阵乘法来表示:
( f X , f Y , Z ) T = ( f 0 0 0 0 f 0 0 0 0 1 0 ) ( X Y Z 1 ) (f X, f Y, Z)^{T}=\left( \begin{array}{cccc}{f} & {0} & {0} & {0} \\ {0} & {f} & {0} & {0} \\ {0} & {0} & {1} & {0}\end{array}\right) \left( \begin{array}{l}{X} \\ {Y} \\ {Z} \\ {1}\end{array}\right) (fX,fY,Z)T=⎝⎛f000f0001000⎠⎞⎝⎜⎜⎛XYZ1⎠⎟⎟⎞
如果相机的CMOS/CCD的位置不在像面的中心位置,则要添加两个参数 p x p_x px和 p y p_y py:
( f X + Z p x , f Y + Z p y , Z ) T = ( f 0 p x 0 0 f p y 0 0 0 1 0 ) ( X Y Z 1 ) \left(f X+Z p_{x}, f Y+Z p_{y}, Z\right)^{T}=\left( \begin{array}{cccc}{f} & {0} & {p_{x}} & {0} \\ {0} & {f} & {p_{y}} & {0} \\ {0} & {0} & {1} & {0}\end{array}\right) \left( \begin{array}{l}{X} \\ {Y} \\ {Z} \\ {1}\end{array}\right) (fX+Zpx,fY+Zpy,Z)T=⎝⎛f000f0pxpy1000⎠⎞⎝⎜⎜⎛XYZ1⎠⎟⎟⎞
现在我们能得到空间上的点在图像坐标系上的坐标位置,但是该坐标的单位是米,我们需要将其转化成像素单位,所以要有比例因子 m x m_x mx、 m y m_y my:
( f m x X + Z m x p x f m y Y + Z m y p y Z ) = ( f m x 0 m x p x 0 0 f m y m y p y 0 0 0 1 0 ) ( X Y Z 1 ) \left( \begin{array}{c}{f m_{x} X+Z m_{x} p_{x}} \\ {f m_{y} Y+Z m_{y} p_{y}} \\ {Z}\end{array}\right)= \left( \begin{array}{cccc}{f_{m_{x}}} & {0} & {m_{x} p_{x}} & {0} \\ {0} & {f m_{y}} & {m_{y} p_{y}} & {0} \\ {0} & {0} & {1} & {0}\end{array}\right) \left( \begin{array}{l}{X} \\ {Y} \\ {Z} \\ {1}\end{array}\right) ⎝⎛fmxX+ZmxpxfmyY+ZmypyZ⎠⎞=⎝⎛fmx000fmy0mxpxmypy1000⎠⎞⎝⎜⎜⎛XYZ1⎠⎟⎟⎞
如果相机CMOS的x轴和y轴不垂直,还要有一个参数 s s s:
K = ( α x S x 0 0 α y y 0 0 0 1 ) K=\left( \begin{array}{ccc}{\alpha_{x}} & {S} & {x_{0}} \\ {0} & {\alpha_{y}} & {y_{0}} \\ {0} & {0} & {1}\end{array}\right) K=⎝⎛αx00Sαy0x0y01⎠⎞
这就是相机的内参数矩阵。
空间的点 P w P_w Pw左乘一个旋转矩阵 R R R,加上旋转矩阵 t t t,得到了该点在相机坐标系上的坐标。再左乘相机的内参数矩阵 K K K就得到了该点在图像坐标系上的像素坐标。
P ~ c = [ X Y Z ] = K ( R P w + t ) \tilde{P}_{c}=\left[ \begin{array}{c}{X} \\ {Y} \\ {Z}\end{array}\right]=K\left(R P_{w}+t\right) P~c=⎣⎡XYZ⎦⎤=K(RPw+t)
至此,针孔相机模型推导完成。
二、鱼眼相机模型
针孔相机的模型为: r d = f tan ( θ ) r_{d}=f \tan (\theta) rd=ftan(θ)
鱼眼相机模型的公式表示为: r d = f θ r_{d}=f \theta rd=fθ
鱼眼相机模型有多种,此处只选择了其中一种
类似针孔相机模型的推导,鱼眼相机成像也很简单。
首先,我们用上面的方法可以得到空间上的点在相机坐标系上的表示。
[ X c Y c Z c 1 ] = [ R 11 R 12 R 13 t 1 R 21 R 22 R 23 t 2 R 31 R 32 R 33 t 3 0 0 0 1 ] [ X w Y w Z w 1 ] \left[ \begin{array}{c}{X_{c}} \\ {Y_{c}} \\ {Z_{c}} \\ {1}\end{array}\right]=\left[ \begin{array}{cccc}{R_{11}} & {R_{12}} & {R_{13}} & {t_{1}} \\ {R_{21}} & {R_{22}} & {R_{23}} & {t_{2}} \\ {R_{31}} & {R_{32}} & {R_{33}} & {t_{3}} \\ {0} & {0} & {0} & {1}\end{array}\right] \left[ \begin{array}{c}{X_{w}} \\ {Y_{w}} \\ {Z_{w}} \\ {1}\end{array}\right] ⎣⎢⎢⎡XcYcZc1⎦⎥⎥⎤=⎣⎢⎢⎡R11R21R310R12R22R320R13R23R330t1t2t31⎦⎥⎥⎤⎣⎢⎢⎡XwYwZw1⎦⎥⎥⎤
简单推导可得:
θ = arctan [ ( X c 2 + Y c 2 ) 1 / 2 Z c ] \theta=\arctan \left[\left(X_{c}^{2}+Y_{c}^{2}\right)^{1 / 2} \over Z_{c}\right] θ=arctan[Zc(Xc2+Yc2)1/2]
这样,就可以得到该点在鱼眼相机图像坐标系上的位置了。
X f i s h = f t a n ( θ ) X c ( X c 2 + Y c 2 ) 1 2 X_{fish} = ftan(\theta){X_c \over (X_{c}^{2}+Y_{c}^{2})^{1\over2}} Xfish=ftan(θ)(Xc2+Yc2)21Xc
Y f i s h = f t a n ( θ ) Y c ( X c 2 + Y c 2 ) 1 2 Y_{fish} = ftan(\theta){Y_c \over (X_{c}^{2}+Y_{c}^{2})^{1\over2}} Yfish=ftan(θ)(Xc2+Yc2)21Yc