ROC(Receiver Operating Characteristic)
AUC(Area Under Curve)
ROC与AUC常用来评价一个二值分类器(binary classifier)的优劣
1.ROC曲线:
只讨论二值分类器。对于分类器,或者说分类算法,评价指标主要有precision,recall,F-score,以及ROC和AUC。下图是一个ROC曲线的示例
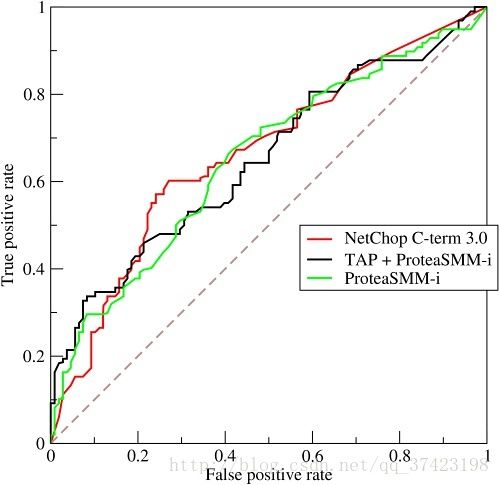
ROC曲线的横坐标为false positive rate(FPR),纵坐标为true positive rate(TPR)
FPR:实例标签为0,被预测为错误的比例
TPR:实例标签为1,被预测为正确的比例
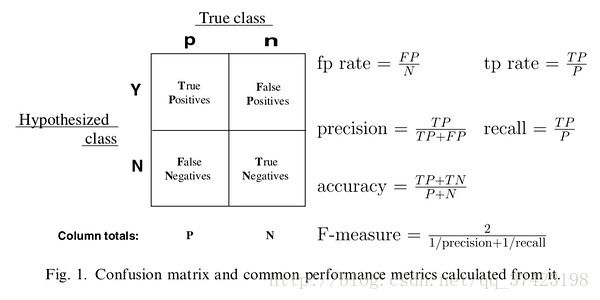
混淆矩阵:

TN:真实值为negative预测为正确(0,0)
FP:真实值为positive预测错误(0,1)
FN:真实值为negative预测错误(1,0)
TP:真实值为positive预测正确(1,1)
ROC曲线图中的四个点和一条线:
第一个点,(0,1),即FPR=0, TPR=1,这意味着FN(false negative)=0,并且FP(false positive)=0,这是一个完美的分类器,它将所有的样本都正确分类
第二个点,(1,0),即FPR=1,TPR=0,类似地分析可以发现这是一个最糟糕的分类器,因为它成功避开了所有的正确答案
第三个点,(0,0),即FPR=TPR=0,即FP(false positive)=TP(true positive)=0,可以发现该分类器预测所有的样本都为负样本(negative)
第四个点(1,1),分类器实际上预测所有的样本都为正样本。
ROC曲线越接近左上角,该分类器的性能越好。
2.绘制ROC曲线
对于一个特定的分类器和测试数据集,显然只能得到一个分类结果,即一组FPR和TPR结果,而要得到一个曲线,我们实际上需要一系列FPR和TPR的值。
示例:
5个样本,真实的类别(标签)是y=c(1,1,0,0,1)
一个分类器预测样本为1的概率p=c(0.5,0.6,0.55,0.4,0.7)
我们需要选定阈值才能把概率转化为类别,如果我们选定阈值为0.1,那么5个样本被分进1的类别,如果选定0.3,结果仍然一样,如果选了0.45作为阈值那么只有样本4被分进0,其余的都进入1类,就可以计算FTR,PTR,把所有得到的所有FTR,PTR绘成线,就可以得到ROC曲线
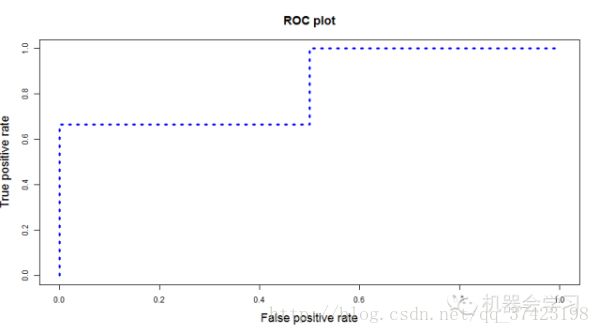
我们根据每个测试样本属于正样本的概率值从大到小排序。下图是一个示例,图中共有20个测试样本,“Class”一栏表示每个测试样本真正的标签(p表示正样本,n表示负样本),“Score”表示每个测试样本属于正样本的概率
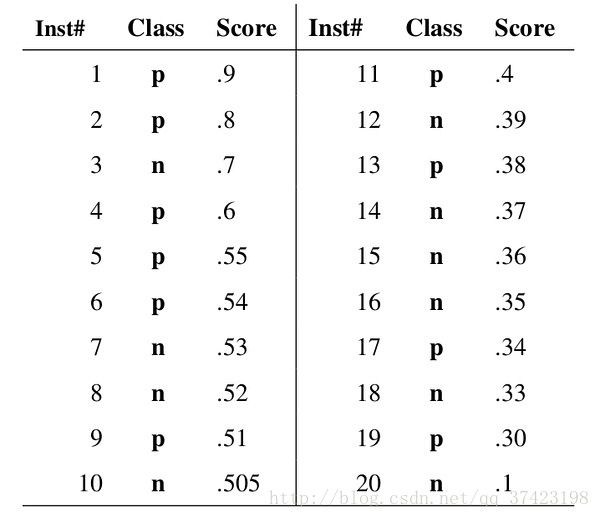
我们从高到低,依次将“Score”值作为阈值threshold,当测试样本属于正样本的概率大于或等于这个threshold时,我们认为它为正样本,否则为负样本。举例来说,对于图中的第4个样本,其“Score”值为0.6,那么样本1,2,3,4都被认为是正样本,因为它们的“Score”值都大于等于0.6,而其他样本则都认为是负样本。每次选取一个不同的threshold,我们就可以得到一组FPR和TPR,即ROC曲线上的一点。这样一来,我们一共得到了20组FPR和TPR的值,将它们画在ROC曲线的结果如下图:
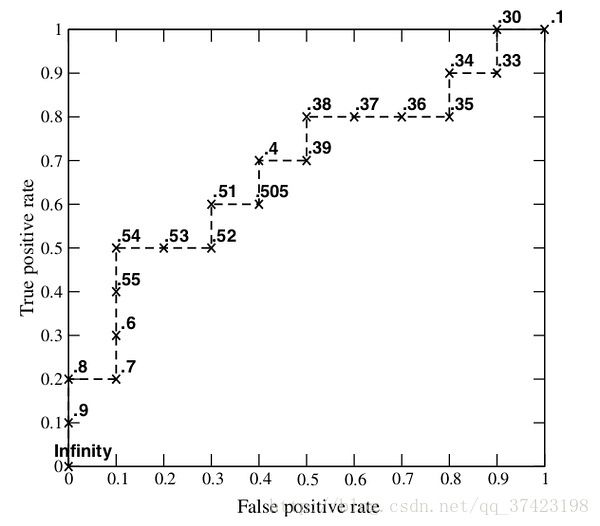
当我们将threshold设置为1和0时,分别可以得到ROC曲线上的(0,0)和(1,1)两个点。将这些(FPR,TPR)对连接起来,就得到了ROC曲线。当threshold取值越多,ROC曲线越平滑。
3.AUC
AUC被定义为ROC曲线下的面积,显然这个面积的数值不会大于1。又由于ROC曲线一般都处于y=x这条直线的上方,所以AUC的取值范围在0.5和1之间。
使用AUC值作为评价标准是因为很多时候ROC曲线并不能清晰的说明哪个分类器的效果更好,而作为一个数值,对应AUC更大的分类器效果更好。
ROC曲线有个很好的特性:当测试集中的正负样本的分布变化的时候,ROC曲线能够保持不变。在实际的数据集中经常会出现类不平衡(class imbalance)现象,即负样本比正样本多很多(或者相反),而且测试数据中的正负样本的分布也可能随着时间变化。

a)和(c)为ROC曲线,(b)和(d)为Precision-Recall曲线。(a)和(b)展示的是分类其在原始测试集(正负样本分布平衡)的结果,(c)和(d)是将测试集中负样本的数量增加到原来的10倍后,分类器的结果。可以明显的看出,ROC曲线基本保持原貌,而Precision-Recall曲线则变化较大。
4.计算代码
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline
parameter = 30
data = pd.DataFrame(index = range(0,parameter),columns = ('probability','The true label'))
data['The true label'] = np.random.randint(0,2,size = len(data))
data['probability'] = np.random.choice(np.arange(0.1,1,0.1),len(data['probability']))
data
cm = np.arange(4).reshape(2,2)
cm[0,0] = len(data[data['The true label']==0][data['probability']<0.5])
cm[0,1] = len(data[data['The true label']==0][data['probability']>=0.5])
cm[1,0] = len(data[data['The true label']==1][data['probability']<0.5])
cm[1,1] = len(data[data['The true label']==1][data['probability']>=0.5])
import itertools
classes = [0,1]
plt.figure()
plt.imshow(cm,interpolation='nearest',cmap=plt.cm.Blues)
plt.title('Confusion matrix')
tick_marks = np.arange(len(classes))
plt.xticks(tick_marks,classes,rotation = 0)
plt.yticks(tick_marks,classes)
thresh = cm.max()/2
for i,j in itertools.product(range(cm.shape[0]),range(cm.shape[1])):
plt.text(j,i,cm[i,j],horizontalalignment='center',color='white' if cm[i,j]>thresh else 'black')
plt.tight_layout()
plt.ylabel('True label')
plt.xlabel('Predicted label')

data.sort_values('probability',inplace=True, ascending=False)
data
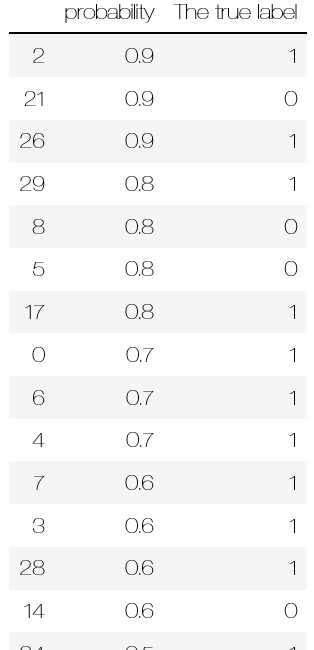
TPRandFPR = pd.DataFrame(index=range(len(data)),columns=('TP','FP'))
for j in range(len(data)):
data1 = data.head(n=j+1)
FP=len(data1[data1['The true label']==0][data1['probability']>=data1.head(len(data1))['probability']])/float(len(data[data['The true label']==0]))
TP=len(data1[data1['The true label']==1][data1['probability']>=data1.head(len(data1))['probability']])/float(len(data[data['The true label']==1]))
TPRandFPR.iloc[j]=[TP,FP]
TPRandFPR
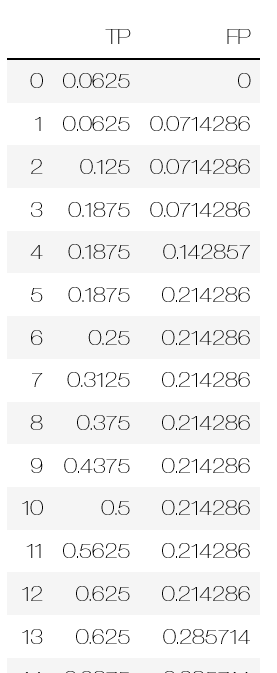
from sklearn.metrics import auc
AUC = auc(TPRandFPR['FP'],TPRandFPR['TP'])
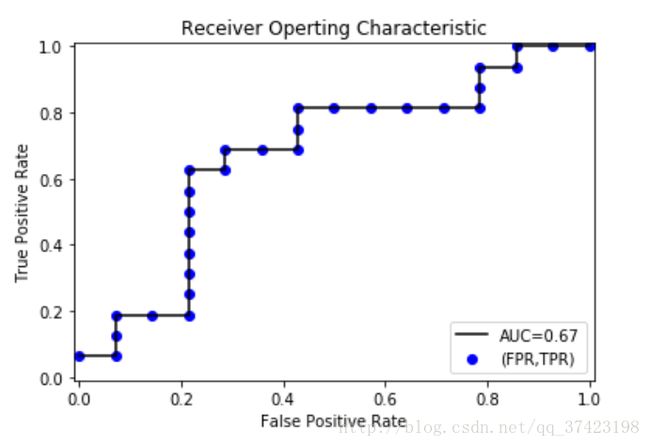
plt.scatter(x=TPRandFPR['FP'],y=TPRandFPR['TP'],label='(FPR,TPR)',color='b')
plt.plot(TPRandFPR['FP'],TPRandFPR['TP'],'k',label='AUC=%0.2f'%AUC)
plt.legend(loc='lower right')
plt.title('Receiver Operting Characteristic')
plt.plot((0,0),(1,1),'r--')
plt.xlim([-0.01,1.01])
plt.ylim([-0.01,1.01])
plt.ylabel('True Positive Rate')
plt.xlabel('False Positive Rate')
plt.show()