python数据分析及特征工程（实战）

本文以天池上面的二手车交易价格预测为例，比赛链接：https://tianchi.aliyun.com/competition/entrance/231784/introduction?spm=5176.12281925.0.0.336a7137z6Duwb

1.数据分析

数据分析阶段也称为探索性数据分析（Exploratory Data Analysis， EDA）。主要用到pandas进行数据分析，相比numpy来说处理数据更加方便。当我们那到数据之后，一般会先通过pandas自带的info，describe，head方法来大致了解一下数据整体结构，例如特征的数据类型，均值方差，以及数值是离散型还是连续性，是否含有空值等。

data = pd.read_csv("../../data/used_car_train_20200313.csv", sep=' ')
#查看特征空值信息，以及数据类型
print(data.info(verbose=True))
#获取特征的均值，标准差，最大最小值，以及分位数
print(data.describe())
#输出数据集前n个样本，默认n=5
print(data.head(n=5)

输出结果如下：通过info函数可以看到bodytype，fueltype，gearbox都是含有空值的，notRepairedDamage是object类型（对应了python中的string数据类型），对于非数值类型一般会转换为数值类型，后面特征工程部分会进行处理；然后describe可以看到特征对应的均值标准差等；然后通过head函数输出前5个样本数据，可以大致了解一下数据整体，我们也可以看到regDate和createDate表示的是年月日的形式，也需要进行处理。看完整体的一个概况我们可以对特征分别进行单个特征和多个特征的分析，得到进一步的信息。

RangeIndex: 150000 entries, 0 to 149999
Data columns (total 31 columns):
SaleID               150000 non-null int64
name                 150000 non-null int64
regDate              150000 non-null int64
model                149999 non-null float64
brand                150000 non-null int64
bodyType             145494 non-null float64
fuelType             141320 non-null float64
gearbox              144019 non-null float64
power                150000 non-null int64
kilometer            150000 non-null float64
notRepairedDamage    150000 non-null object
regionCode           150000 non-null int64
......

              SaleID           name       regDate          model          brand       bodyType       fuelType        gearbox          power      kilometer     regionCode         seller  offerType     creatDate          price            v_0            v_1            v_2            v_3            v_4            v_5            v_6            v_7            v_8            v_9           v_10           v_11           v_12           v_13           v_14
count  150000.000000  150000.000000  1.500000e+05  149999.000000  150000.000000  145494.000000  141320.000000  144019.000000  150000.000000  150000.000000  150000.000000  150000.000000   150000.0  1.500000e+05  150000.000000  150000.000000  150000.000000  150000.000000  150000.000000  150000.000000  150000.000000  150000.000000  150000.000000  150000.000000  150000.000000  150000.000000  150000.000000  150000.000000  150000.000000  150000.000000
mean    74999.500000   68349.172873  2.003417e+07      47.129021       8.052733       1.792369       0.375842       0.224943     119.316547      12.597160    2583.077267       0.000007        0.0  2.016033e+07    5923.327333      44.406268      -0.044809       0.080765       0.078833       0.017875       0.248204       0.044923       0.124692       0.058144       0.061996      -0.001000       0.009035       0.004813       0.000313      -0.000688
std     43301.414527   61103.875095  5.364988e+04      49.536040       7.864956       1.760640       0.548677       0.417546     177.168419       3.919576    1885.363218       0.002582        0.0  1.067328e+02    7501.998477       2.457548       3.641893       2.929618       2.026514       1.193661       0.045804       0.051743       0.201410       0.029186       0.035692       3.772386       3.286071       2.517478       1.288988       1.038685
min         0.000000       0.000000  1.991000e+07       0.000000       0.000000       0.000000       0.000000       0.000000       0.000000       0.500000       0.000000       0.000000        0.0  2.015062e+07      11.000000      30.451976      -4.295589      -4.470671      -7.275037      -4.364565       0.000000       0.000000       0.000000       0.000000       0.000000      -9.168192      -5.558207      -9.639552      -4.153899      -6.546556
25%     37499.750000   11156.000000  1.999091e+07      10.000000       1.000000       0.000000       0.000000       0.000000      75.000000      12.500000    1018.000000       0.000000        0.0  2.016031e+07    1300.000000      43.135799      -3.192349      -0.970671      -1.462580      -0.921191       0.243615       0.000038       0.062474       0.035334       0.033930      -3.722303      -1.951543      -1.871846      -1.057789      -0.437034
50%     74999.500000   51638.000000  2.003091e+07      30.000000       6.000000       1.000000       0.000000       0.000000     110.000000      15.000000    2196.000000       0.000000        0.0  2.016032e+07    3250.000000      44.610266      -3.052671      -0.382947       0.099722      -0.075910       0.257798       0.000812       0.095866       0.057014       0.058484       1.624076      -0.358053      -0.130753      -0.036245       0.141246
75%    112499.250000  118841.250000  2.007111e+07      66.000000      13.000000       3.000000       1.000000       0.000000     150.000000      15.000000    3843.000000       0.000000        0.0  2.016033e+07    7700.000000      46.004721       4.000670       0.241335       1.565838       0.868758       0.265297       0.102009       0.125243       0.079382       0.087491       2.844357       1.255022       1.776933       0.942813       0.680378
max    149999.000000  196812.000000  2.015121e+07     247.000000      39.000000       7.000000       6.000000       1.000000   19312.000000      15.000000    8120.000000       1.000000        0.0  2.016041e+07   99999.000000      52.304178       7.320308      19.035496       9.854702       6.829352       0.291838       0.151420       1.404936       0.160791       0.222787      12.357011      18.819042      13.847792      11.147669       8.658418

   SaleID    name   regDate  model  brand  bodyType  fuelType  gearbox  power  kilometer notRepairedDamage  regionCode  seller  offerType  creatDate  price        v_0       v_1       v_2       v_3       v_4       v_5       v_6       v_7       v_8       v_9      v_10      v_11      v_12      v_13      v_14
0       0     736  20040402   30.0      6       1.0       0.0      0.0     60       12.5               0.0        1046       0          0   20160404   1850  43.357796  3.966344  0.050257  2.159744  1.143786  0.235676  0.101988  0.129549  0.022816  0.097462 -2.881803  2.804097 -2.420821  0.795292  0.914762
1       1    2262  20030301   40.0      1       2.0       0.0      0.0      0       15.0                 -        4366       0          0   20160309   3600  45.305273  5.236112  0.137925  1.380657 -1.422165  0.264777  0.121004  0.135731  0.026597  0.020582 -4.900482  2.096338 -1.030483 -1.722674  0.245522
2       2   14874  20040403  115.0     15       1.0       0.0      0.0    163       12.5               0.0        2806       0          0   20160402   6222  45.978359  4.823792  1.319524 -0.998467 -0.996911  0.251410  0.114912  0.165147  0.062173  0.027075 -4.846749  1.803559  1.565330 -0.832687 -0.229963
3       3   71865  19960908  109.0     10       0.0       0.0      1.0    193       15.0               0.0         434       0          0   20160312   2400  45.687478  4.492574 -0.050616  0.883600 -2.228079  0.274293  0.110300  0.121964  0.033395  0.000000 -4.509599  1.285940 -0.501868 -2.438353 -0.478699
4       4  111080  20120103  110.0      5       1.0       0.0      0.0     68        5.0               0.0        6977       0          0   20160313   5200  44.383511  2.031433  0.572169 -1.571239  2.246088  0.228036  0.073205  0.091880  0.078819  0.121534 -1.896240  0.910783  0.931110  2.834518  1.923482

1.1单属性分析

1.1.1 异常值分析

（1）连续值的异常值
对于连续值来说，对于那些过大的数据值或太小的数据值对整体都会有很大的影响，不能很好地表现真实情况。例如在反映公司的人均收入时，少部分人的年薪可能达到1000w甚至更高，而大部分公司职员的收入都在中等水平，而这些较大值在统计公司人均收入水平时就会起到一个很大的拔高作用，使得失去了意义。

对于连续异常值的判断标准是我们通常会设置一个上界和下界，在上下界之外的都属于异常值，而这个上下界的设定如下：设q_low和q_high分别为数据的下四分位数和上四分位数，value_low和value_high分别为下界和上界，那么value_low=q_low-k*(q_high-q_low)，value_high=q_high+k*(q_high-q_low)，k通常取值1.5或3。

对于连续异常值的处理可以直接去掉（异常值不多的情况），也可以用边界值代替异常值。空值也可以作为异常值进行处理，对于连续值属性可以用均值来代替空值。

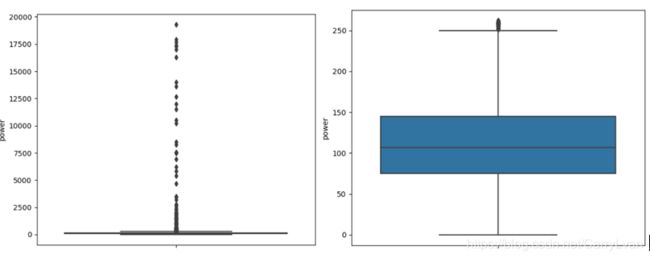
现在对上面的power特征进行异常值分析，这里加入可视化展示，通过可视化可以让数据更加直观，这里用到的是seaborn中的箱线图。

plt.figure()
sns.boxplot(y=data["power"])
plt.show()

q_low = data["power"].quantile(q=0.25)
q_high = data["power"].quantile(q=0.75)
q_interval = q_high - q_low
index_high = data["power"] <= (q_high + 1.5 * q_interval)
index_low = data["power"] >= (q_low - 1.5 * q_interval)

print("异常值样本数量：",len(data)-len(data[index_low & index_high]))

plt.figure()
sns.boxplot(y=data["power"][index_low & index_high])
plt.show()

结果如下：

（2）离散值的异常值
离散异常值主要为那些在我们特征属性定义之外的值，例如空值，或者我们定义了工资水平为高中低三种值但却出现了其他值，这些都是异常值。对于异常值在数量不大的时候我们都可以直接删除掉，对于空值和异常值可以使用众数来代替也可以把控制当做一个单独的值进行处理。

现在我们对上面的notRepairedDamage进行分析：我们通过value_counts查看离散属性每个值的数量，我们发现除了0和1之外我们发现出现了“-”，而通过题目给出的含义我们知道notRepairedDamage只有0 1两类取值，因此我们可以用众数来替换，也可以直接用nan空值来替换，因为如果建模阶段采用树模型是可以不对空值处理的

print(data['notRepairedDamage'].value_counts())

结果：

0.0    111361
-       24324
1.0     14315
Name: notRepairedDamage, dtype: int64

（3）知识异常值
知识异常值是指在尝试范围或限定知识范围外的值都是知识异常值，例如身高出现了3米4米，或者题目给定了某些特征的取值范围，例如题目给出了power发动机的范围是0~600，那么我们对power的处理其实不需要向上面那样来确定上下界，因为题目已经给出了。

1.1.2 分布分析

1.如何判断是不是正态分布？
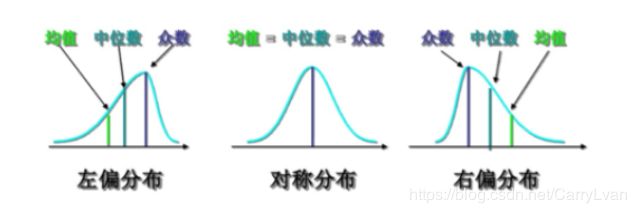
对于获得的数据我们可以直接获得其概率分布，但是这样的得到的分布往往意义不大，所以我们通产常会判断它是否服从正态分布。通常我们会通过数据的偏度和峰度来判断是否是正态分布，偏度系数是数据平均值偏离状态的一种衡量，对于对称性分布而言平均值和中位数是比较接近的（例如正态分布），而非对称分布中位数和均值相差较大，这种分布也叫做有偏态的分布。
（1）偏度系数大于0，正偏（右偏），均值较大（相对于中位数而言）
（2）偏度系数小于0，负偏（左偏），均值较小
正态分布的峰度系数为3，如果某个分布的峰度系数与正态分布的峰度系数相差超过2，那么这个分布就不是正太分布。

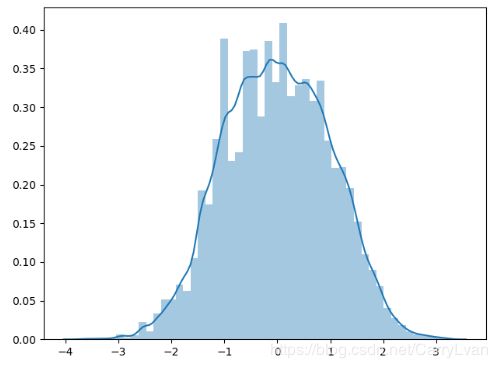
我们可以看一下上面的price属性，通过峰度系数和直方图能明显看出是一个正偏的分布。

print("偏度系数：",data["price"].skew())
print("峰度系数：",data["price"].kurtosis())

plt.figure()
sns.distplot(data["price"])
plt.show()

输出结果：

偏度系数： 3.3464867626369608
峰度系数： 18.995183355632562

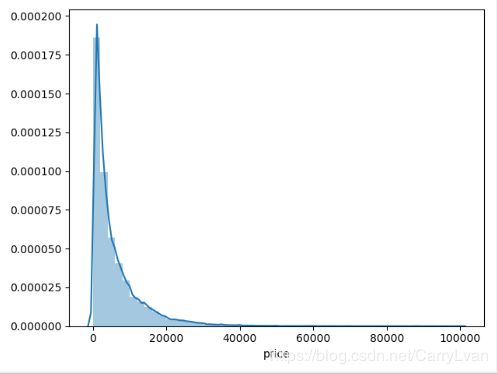
通常我们会将偏态的分布转为正态分布，但是也并不是什么时候都需要，下面可以看一下什么情况比较适合做正态分布在转换。

2.为什么要转换为正态分布？
（1）首先有些模型的应用条件就是要求你的数据满足正态性分布的，比如说贝叶斯、逻辑回归、KNN、Kmean等涉及到概率分布、参数距离比较等，转换为正态分布，模型条件更充足。但并不意味着你的模型结果会更好一点。
（2）其次正态分布，数据的泛化性高。因为自然界很多事物的概率密度很大是正态分布，而偏态分布（数据不均衡），会导致机器学歪了，用这个“歪”模型测试数据不会很靠谱。
（3）从目标分布来说，偏态分布会导致label数据的MSE出现误导，或许结果看着很小，但实际结果很大，可以考虑纠正一下分布正态性。

3.什么情况下做正态分布转换？
（1）并不是说所有分布都要转换为正态分布的，因为你不能保证正态分布就很有效，其次不是所有数据分布都类似于正态分布，可能是其他乱七八槽的分布，又或许是大数定理下的分布渐进正态性。（比如泊松分布、卡方分布等），这些非正态分布就没必要转换。
（2）偏态分布最好纠正，或许有用（理论上有用，实际上可能没用，因为数据量的分布限制）。这就好比于“你打个喷嚏可以吃板蓝根，或许有用，或许没用，但绝对不会导致你喷嚏更加严重”，就是说针对偏态分布，你可以正态化一下。

4.常见的转换方式

接着分析一下上面的price属性，这里我们可以通过seaborn中的distplot函数中的fit参数拟合更符合哪种分布，方便后面进行转换。

plt.figure()
sns.distplot(data["price"],fit=ss.lognorm)
plt.show()

plt.figure()
sns.distplot(data["price"],fit=ss.norm)
plt.show()

plt.figure()
sns.distplot(data["price"],fit=ss.johnsonsu)
plt.show()

输出结果：



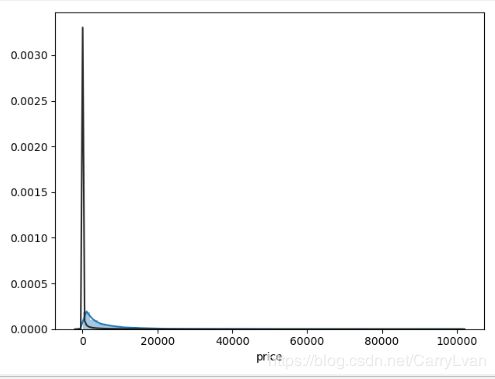
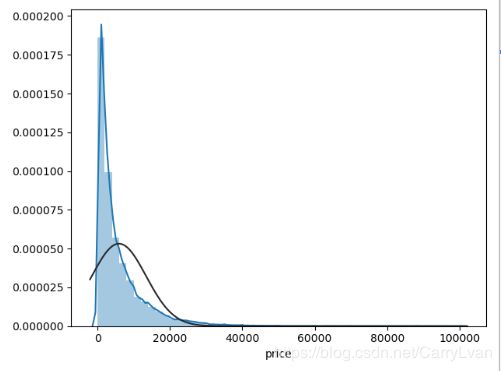
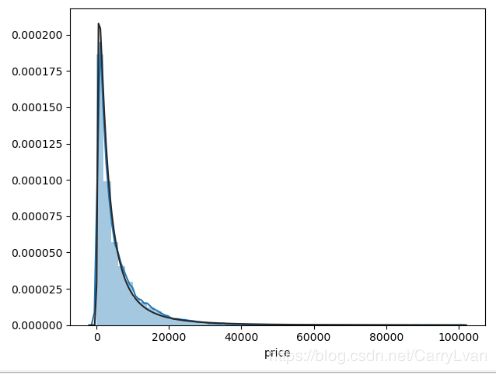
通过上面的结果可以看到无界约翰逊分布的拟合效果更好，因此在做分布转换时，可以利用sklearn.preprocessing包里的power_transform进行转换，如下：

yc_data = power_transform(X=np.array(data["price"]).reshape(-1,1),method="yeo-johnson")

plt.figure()
sns.distplot(yc_data)
plt.show()

输出结果：可以看到转换后的正态分布如下

1.1.3 对比分析

（1）绝对数比较：例如比较收入或身高等属性。
（2）相对数比较：把几个有联系的指标联合构成新的数，主要有以下几种类别：

• 结构相对数：部分与整体进行相比，例如用产品合格率评估产品质量。
• 比例相对数：总体内用不同部分的数值进行比较，例如传统三大产业：农业、重工业和服务业之间的比例可以进行相互比较。
• 比较相对数：同一时空下相似或同质的指标进行对比，例如不同互联网公司的待遇水平或者不同时期同一商品的价格比较。
• 动态相对数：一般具有时间概念，例如速度、用户数量的增速。
• 强度相对数：性质不同但又相互联系的属性进行联合，例如人均GDP、密度等。

那么有了这些基本的概念属性之后如何进行比较呢？大致可以从以下几个维度进行比较分析：

1. 时间维度：现在和过去进行比较等进而推断未来的走势。其中有“同比”和“环比”两种方式，“同比”是和去年同期进行比较，例如今年某汽车销量同比增加百分之几；“环比”：例如今年6月份汽车销量环比是和今年5月份进行比较。
2. 空间维度：可指现实方位上的空间，例如不同城市、不同国家·；也可指逻辑上的空间，例如一家公司的不同部门进行比较。
3. 经验和计划：经验比较：例如历史上失业率发生百分之几就可能发生暴乱，我们把自己国家的失业率和这个进行比较就是经验比较；计划比较：是指实时速度和计划排期进行比较。

1.1.4 结构分析

研究一个总体的组成结构方面的差异和相关性。
（1）静态结构分析：直接分析总体的组成。例如直接分析第一产业、第二产业、第三产业的比例为13%，46%，41%，这样就确定了我国的产业结构，同时和美国、日本等进行比较，来衡量我们三大产业是否均衡，下一步如何决策等。

（2）动态结构分析：以时间为轴分析结构变化的趋势。例如知道十五期间三大产业的占比，那么对于十一五期间三大产业的结构是如何变化的就能够反映国家性质上的反应方向。

1.2多属性分析

1.2.1假设检验

原理：
（1）假设检验含有原假设和备择假设，一般是将我们想拒绝的假设作为原假设。这个时候引出我们的推断原理：小概率事件在一次实验中实际是不可能发生的，如果小概率事件发生了，则与推断原理矛盾，那么就拒绝原假设。
（2）那么概率小于多少时可认为小概率事件？在假设检验中，设这个概率为$\alpha$，也称为显著性水平，$\alpha$常取的值为0.01，0.05，0.1。

假设检验的流程：

• 提出假设：H0（原假设），H1（备择假设）
• 构造检验统计量（这也是不同假设检验的区别之处）：例如$u$检验统计量：$u=\frac{x-{\mu }_0}{\sigma /\sqrt{}n}$
• 给定显著性水平$\alpha$
• 作出假设：若原假设H0为真，那么备择假设H1就是小概率事件。称w：$\{|u|>u_{\alpha /2}\}$为拒绝域，若我们的检验统计量落在区域w内，则拒绝H0，否则没有充分的证据拒绝H0，其中$u_{\alpha /2}$通过查表获得。

python中scipy.stats给我们提供了假设检验的一些方法，我们可以检验是否为正态分布、利用卡方检验来进行两个及两个以上样本率( 构成比）以及两个分类变量的关联性分析、利用t检验来检验两组数据均值是否有差异、以及通过f检验多组数据的方差是否有差异。

例如我们可以利用卡方检验来进行判断公司中员工是否离职与部门之间是否有关系，更多卡方检验的知识可以参考统计学——卡方检验和卡方分布，举个栗子：

import numpy as np
import pandas as pd
import scipy.stats as ss

norm_dist = ss.norm.rvs(size=1000)
# 检验是否为正态分布
print(ss.normaltest(norm_dist))
# 卡方检验
print(ss.chi2_contingency([[15,95],[85,5]]))
# 检验两组分布的均值是否有差异
print(ss.ttest_ind(ss.norm.rvs(size=10), ss.norm.rvs(size=20)))
# 方差检验，检验多组数据的方差是否有差别
print(ss.f_oneway([49,50,39,40,43],[28,32,30,26,34],[38,40,45,42,48]))

1.2.2 相关系数

相关系数是用来衡量两组数据或者两组样本的分布趋势、变化趋势、一致性程度的因子，分为正相关、负相关、不相关。

常见的相关系数有：
Pearson相关系数：$r(X,Y)=\frac{Cov(X,Y)}{{\sigma }_x{\sigma }_y}$，Cov(X,Y)为X，Y的协方差，σ为标准差。
Spearman相关系数：${\rho }_s=1-\frac{6\ast \sum d_i^2}{n(n^2-1)}$，n是数据数量，d是两组数据排名的名次差。例如x={6,11,8} y={7,4,3}，rank_x={1,3,2}，rank_y={3,2,1}，d={-2,1,1}。

我们通常会分析label数据和特征之间的相关性，对于那些不怎么相关的特征可以去掉。例如我们分析price和特征之间的关系。

correlation = data.corr()
print(correlation['price'].sort_values(ascending = False))
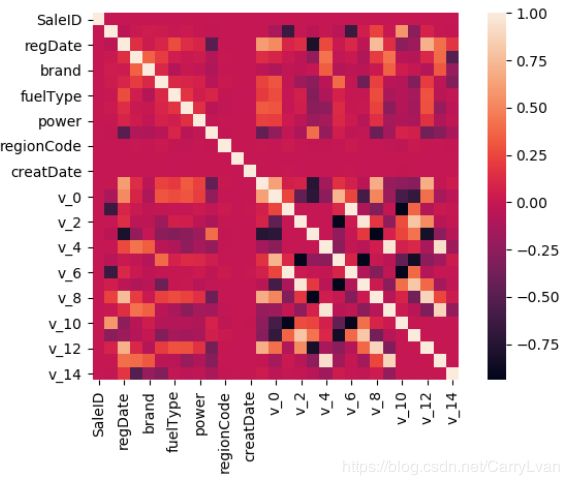
plt.figure()
sns.heatmap(correlation,square = True)
plt.show()

输出结果：

price         1.000000
v_12          0.692823
v_8           0.685798
v_0           0.628397
regDate       0.611959
gearbox       0.329075
bodyType      0.241303
power         0.219834
fuelType      0.200536
v_5           0.164317
model         0.136983
v_2           0.085322
v_6           0.068970
......

1.2.3 主成分分析PCA

PCA通常也是特征降维的一种手段。我们可以直接使用sklearn提供的pca进行降维处理。就先放到后面特征工程中的降维一起讲。

2.特征工程

2.1 数据清洗

这部分其实就和分析部分的异常值分析一样，我们会对异常值和空值进行处理，其实数据分析部分和特征工程并不是完全独立的，分析就是为了更好地了解数据，更好的完成特征工程。对于异常值的处理就跟前面所说一样，空值可以删除也可以进行填充。

#缺失值处理：离散值用众数处理，连续值用均值填充。
values = {"bodyType": data["bodyType"].value_counts().index[0], "fuelType":data["fuelType"].value_counts().index[0],
              "gearbox": data["gearbox"].value_counts().index[0], "model": data["model"].mean()}
data.fillna(value=values, inplace=True)

2.2 特征选择

在我们拿到数据之后，除了向开头那样了解数据大致结构之外，我们还通常会查看离散值的value_counts，除了查看是否存在异常值之外，还会看离散值的分布是否均衡。

例如通过查看offerType和seller的value_counts我们发现这两个特征其实对于预测价格并没有什么作用，所以可以直接删掉。

print(data["offerType"].value_counts(),"\n")
print(data["seller"].value_counts())

输出结果：

0    150000
Name: offerType, dtype: int64 

0    149999
1         1
Name: seller, dtype: int64

当然会有一些常用的特征选择思路：过滤思想（Filter），包裹思想（Wrapper），嵌入思想（Embedding）。

• 过滤思想：直接评价特征与标注的相关性，如果相关性比较小就去掉。
• 包裹思想：设特征集合为X：{x1, x2, …, xn}。最佳特征组合是其子集，目的就是找到这个子集，首先需要设定一个评价指标，例如准确率，然后遍历特征子集找到准确率最高的。也可以进行迭代操作，例如先确定几个较大的子集，然后确定一个较大子集之后对其进行继续拆分，直到评价指标下降过快或低于阈值时停止。
• 嵌入思想：常用的方式就是正则化。

from sklearn.svm import SVR
from sklearn.tree import DecisionTreeRegressor
from sklearn.feature_selection import SelectKBest,RFE, SelectFromModel
#SelectKBest是过滤思想常用的包， RFE是包裹思想， SelectFromModel是嵌入思想
features = [col for col in data.columns if col not in ['price','SaleID']]
X = data.loc[:,features]
Y = data.loc[:,"price"]
#过滤思想
skb = SelectKBest(k=8)
skb.fit(X,Y)
print(skb.transform(X).shape)
#包裹思想
rfe = RFE(estimator=SVR(kernel="linear"), n_features_to_select=8, step=1)
print(rfe.fit_transform(X,Y).shape)
#嵌入思想
#特征重要性或特征系数小于threshold将被舍弃
sfm = SelectFromModel(estimator=DecisionTreeRegressor(), threshold=0.1)
print(sfm.fit_transform(X,Y))

2.3 特征变换

• 指数化：$f(x)=e^x$，当大于0范围内原始数据差距很小，经过指数变换后数据差距边大。
• 对数化：$f(x)=lnx$，当在大于1的范围内数据变化很大时，变换后差距变小，可以将一个大的数缩放到我们容量计算的范围内。例如，月收入1亿、10000，1000直接通过乘除比较容易丢失精度，经过log10X变换后得到8，4，3，然后可以得到数据的大小关系。
• 离散化：将连续变量分成几段（bins），数据分桶。
• 归一化：min-max：$x^{\prime }=\frac{x-x_{min}}{x_{max}-x_{min}}$；z-score：$x^{\prime }=\frac{x-\mu }{\sigma }$
• 数值化：（1）标签化，例如将收入水平low, medium, high转换为0，1，2；（2）独热编码：例如对颜色特征进行独热编码，red:[1,0,0,0]，yellow:[0,1,0,0]，blue:[0,0,1,0]，green:[0,0,0,1]

例如我们对题目中的model和power进行分桶操作：

#将连续值离散化：数据分桶
bin = [i * 10 for i in range(-1,61)]
print(bin)
data['power_bin'] = pd.cut(data['power'], bin, labels=False)

bin = [i * 10 for i in range(-1,26)]
print(bin)
data['model_bin'] = pd.cut(data['model'], bin, labels=False)

2.4 特征构造

特征构造部分也是特征工程的一个难点，没有固定的一些流程方法，但是有一些经验性的东西可以也借鉴一下。例如对于时间特征我们可以进行相减得到时间差，也可以进行不同特征之间的交叉。
例如，通过特征交叉，使用分类特征“brand”、“model”、等与“price”、“days”、“power”进行特征交叉，在最终使用的时候我们会选择真正有用的特征：

data_gb = data.groupby("brand")
all_info = {}
for kind, kind_data in data_gb:
    info = {}
    kind_data = kind_data[kind_data['price'] > 0]
    info['brand_amount'] = len(kind_data)
    info['brand_price_max'] = kind_data.price.max()
    info['brand_price_median'] = kind_data.price.median()
    info['brand_price_min'] = kind_data.price.min()
    info['brand_price_sum'] = kind_data.price.sum()
    info['brand_price_std'] = kind_data.price.std()
    info['brand_price_mean'] = kind_data.price.mean()
    info['brand_price_skew'] = kind_data.price.skew()
    info['brand_price_kurt'] = kind_data.price.kurt()

    all_info[kind] = info

brand_fe = pd.DataFrame(all_info).T.reset_index().rename(columns={"index": "brand"})
data = data.merge(brand_fe, how='left', on='brand')

2.5 特征降维

除了PCA降维之外，我们还可以用LDA降维（Linear Discriminant Analysis，线性判别式）。降维并不等同于特征选择，降维本质上是从一个维度空间映射到另一个维度空间，特征的多少别没有减少，当然在映射的过程中特征值也会相应的变化。

features = [col for col in data.columns if col not in ['price','SaleID']]
X = data.loc[:,features]
Y = data.loc[:,"price"]
from sklearn.decomposition import PCA
lower_dim = PCA(n_components=8)
print(lower_dim.fit_transform(X))

from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
print(LinearDiscriminantAnalysis(n_components=8).fit_transform(X,Y))

参考博客：
统计学——卡方检验和卡方分布
机器学习中特征降维和特征选择的区别