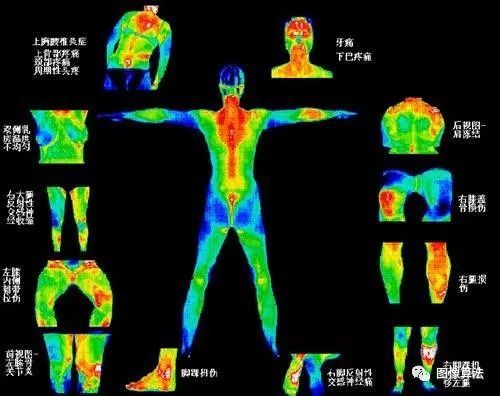
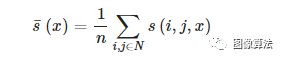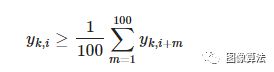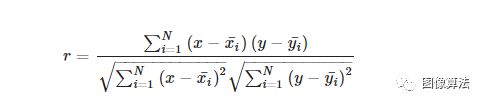如何使用远红外热成像仪估分析犯罪现场留在地面上的热脚印

 

最近新冠状病毒把热成像仪搞火了，价格非常昂贵，以后量大了价格估计会比较亲民。

 

今天我们就来看一篇跟热成像相关的文章，这篇文章是由海康、华师大、上交大以及教育部人工智能重点实验室联合发布。

 

背景 

当前科学技术的进步在解决疑难案件中发挥着越来越重要的作用。热像仪可以捕获肇事者在地面上留下的热量痕迹，用肉眼无法发现这些痕迹，从而可以帮助警察破获困难的案件。因此，本研究的目的是使用热成像系统建立热足模型来估计出发时间。我们使用热像仪获取残留在地板上的热序列，并通过图像处理算法将其转换为热信号。建立了热足迹印刷模型，因为我们观察到残余温度将根据牛顿冷却定律随离开时间呈指数下降。从相应的107个热信号得出的107个热足模型的相关系数基本上高于0.99。在验证实验中，进行了残差分析，估计的出发时间点与地面真相时间之间的残差几乎在-150 s至+150 s的某个范围内。估计起飞时间分别为三分之一，二分之一，三分之二，三分之四，五分之四和五分之六的Thermalfoot模型的反向精度为71.96％，50.47％，42.06％，31.78 ％，21.70％和11.21％。

 

两种主观评价方法的比较实验结果

主观1：根据获得的局部曲线直接估计出发时间；

主观2：利用辅助工具（例如尺子）根据获得的局部曲线估算出发时间），进一步证明了热脚模型对反向检测出发时间的有效性。

 

实验结果还表明，热脚模型在某人离开的短时间窗口内的出发时间反转上具有良好的性能，而通过热脚模型在某人离开的长时间窗口内准确确定出发时间可能只有大约15％。离群值，ROI（感兴趣区域）的选择，ROI的大小，不同的捕获时间点和环境温度对热脚模型在出发时间反转上的性能的影响可以在未来的工作中探索。总体而言，“热脚”模式可以帮助警察在一定程度上解决犯罪问题。

 

关键字

热成像 刑事侦察; 牛顿冷却定律；热痕分析

 

介绍

随着科学技术的发展，犯罪手段越来越多样化，犯罪分子的反侦察意识越来越强，犯罪现场越来越复杂。由于当时的技术局限，过去的一些困难案例仍未解决。在高科技犯罪的趋势下，警察的刑事侦查能力面临着新的突破性挑战。在智能时代的背景下，为了满足人们对社会的安全和稳定发展的需求，许多科学家在相关领域已经研究了多种先进的侦查手段，如法医DNA分析技术，测谎检测技术基于信息分析，以及微量物证识别技术。DNA分析技术利用残留在犯罪现场的DNA来识别具有高度匹配度和敏感性的犯罪分子。但是，在某些极端情况下，犯罪现场的DNA数量很少甚至没有DNA残留。

测谎仪检测技术可以帮助识别犯罪活动的真实性。例如，一部名为《对我说谎》的戏剧电影的编剧塑造了一个人类测谎仪角色，可以识别任何人的谎言。这部电影的主人公卡尔·莱特曼博士可以通过微表情识别技术轻松读取人们的内在秘密。但是，在现实生活中，测谎的结果会受到测试人员的主观因素的极大影响，测试人员可以使用伪装等反检测方法来大大降低测谎技术的性能。

 

痕量材料证据识别技术可用于通过在犯罪现场捕获痕量材料证据来解决犯罪，但是此技术的取证有效性很大程度上取决于在犯罪现场收集的零碎证据的完整性。总之，不同的刑事侦查技术具有不同的技术弱点。

 

热成像技术是一种被动式成像技术。在某些条件下，它可以充分发挥其技术优势，并与其他技术形成优势互补，以协助发现困难案件。通过使用热成像技术收集施暴者脚部接触的地面图像，可以获得温度下降的曲线，因此我们可以通过反向推断来确认施暴者离开的时间。与其他刑事侦查技术相比，测试人员的心理因素对热成像技术的性能没有影响，对硬件架构和测试环境的要求相对较低。但是具有受时间限制的缺点。也就是说，犯罪发生后，随着时间的流逝，地面上的余热逐渐达到环境温度时，该技术将在某种程度上失效。

 

远红外热成像已被广泛用于在远程医疗呼吸监测，障碍物检测和行人检测在智能交通，在智能业故障检测，消防安全智能城市，体温检测等。

 

在刑事调查，一个人的面部图像可以通过热成像技术来获得，然后相关的分析可以进行以确定该人是否有欺诈行为。此后热成像技术已被常用于安全检查。

当然热成像技术也可以用于密码破解。用热序列图像建立物理模型，用于破解密码，然后通过反演算法对密码进行破解，密码破解的准确率达到26％。

 

也有论文描述利用热量跟踪技术研究了破解手机的解锁密码和解锁模式的可行性，研究结果表明，即使重复解锁密码，其破解精度也高于72％。但是，他们的文章缺乏有效的物理模型来解释裂纹过程。这种现象就像人类手中的火，可以用来理解人类的某些行为模式。

现有的相关文献主要集中在如何通过手留下的余热来破解代码。据我们所知，所报道的技术均未采用热成像技术来测量热足迹（脚在地面上留下的热序列）以反向检测时间轨迹。因此，通过对热足迹模型的研究，我们发现了地面上看不见的残余温度信息与出发时间之间的重要关系。

 

热足迹是一种犯罪痕迹，很容易被忽略并且很难迅速消除。在特定时间范围内，警察可以利用犯罪现场留下的热量足迹来捕获有关犯罪的时间信息。如果时间窗口太长，警察无法获得很多有用的热脚信息。微弱的热量痕迹可用于推断犯罪分子的目标和逃生路线，这对缩小犯罪嫌疑人的范围非常重要。另外，我们相信，随着技术的发展，热像仪变得越来越便宜，可以安装在更多的地方，例如银行，超市，一些房屋以及消费者使用的移动终端。当犯罪发生时，热像仪可以及时捕获热量痕迹，而无需警察的帮助。通过进一步研究，可以将一些智能系统连接到热像仪，这些系统可以自动提取热迹线的ROI，输出出发时间或其他有用信息。因此，成功应用热足迹技术无疑将为警察破案提供有价值的信息，并在一定意义上促进智能公共安全的发展。

 

研究目标

（1）获取脚印的热序列并基于牛顿冷却定律建立热足模型;

（2）设计验证实验，以评估热足模型在估计出发时间方面的有效性；

（3）将热脚模型的性能与两种主观计算方法对出发时间反转的性能进行比较

（4）讨论可能影响热脚模型性能的几个因素。

 

方法

• Thermalfoot框架

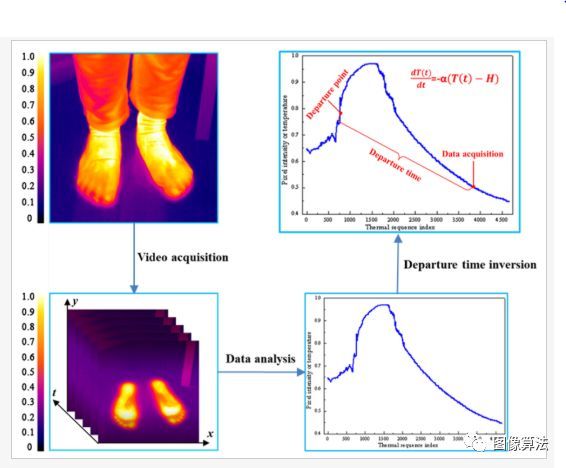
如图1所示，当受试者在地板上行走时，由于地面和人脚之间的温差，热痕迹会留在地板上。我们将其定义为“热足迹”。

 

图1. 出发时间估计方案。

热成像是一种被动成像技术，它可以记录绝对温度高于零的物体发出的能量，而无需任何外部刺激，例如有害的辐射和照明等。

 

考虑到远红外波段的特性，热成像仪能够捕获该热迹线，从而获得一组热序列。通过预处理，热序列可以转换为一维热足迹打印信号。根据牛顿的冷却定律，地板上的残留热量将随着时间逐渐减少，因此该曲线呈指数下降趋势，最终基本保持不变。我们根据牛顿冷却定律获得了时间和温度模型。如果我们可以在特定的时间范围内访问热敏脚印信息，则可以使用获得的模型通过反分析来确定对象的离开时间。

 

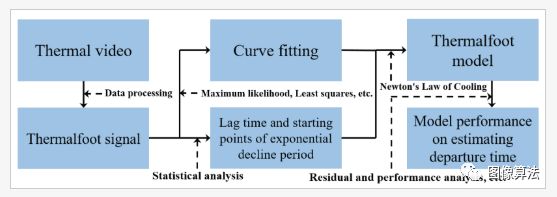
本文的总体算法流程图如图2所示。

图2.提出的算法的工作流程。

通过热成像仪获得热视频，我们采用一系列数据处理方法获得一维热足打印信号。

 

用热敏足印信号进行了两种处理：

（1）通过定性分析，我们发现其中存在两个独特的特征，即滞后时间和指数下降期的起点。在模型的实际应用中，完全不可能准确或精确地测量滞后时间和指数下降期的起点。因此，我们必须对这两个变量进行统计分析，以根据先验知识在某些限制下得出它们的可能值；

（2）在指数下降期，为简化问题，我们将非凸优化更改为凸优化，并假设噪声项符合高斯分布。随后，通过基于最大似然法和最小二乘法的算法对曲线进行拟合，建立温度和时间的指数递减关系式。要在估算出发时间时评估模型性能，

• 实验数据采集

我们使用巨哥热成像仪获取实验场景的热视频，并删除异常数据后，通过图像处理从热视频中提取了100多组热曲线。已对热像仪进行了纠正。热像仪的光谱范围和热灵敏度为7.5至14μm和0.5 ∘C分别。输出的热图像以BitMaP格式存储。温度测量范围为−20∘C到150 ∘C，温度分辨率为1 ∘C，表示热像仪的可靠性。在实验过程中，参与者站立在地板上，脚上踩着袜子一段时间。在他们离开后，我们开始使用热像仪在足迹轨迹上记录视频，以获取热序列以用于后续分析。参与者的体重在45至80公斤之间，环境温度为16∘C到28 ∘C.我们限制了地板的材料和受试者的站立时间，因为该地板是一种普通的木质地板，站立时间分别为30到180s。

 

在我们的实验中，所有受试者都穿着袜子，这与实际应用更为吻合。考虑到犯罪情况，犯罪者不会倾向于穿鞋以防止残留物，例如地面上的污渍。另外，赤脚会导致体液残留在地面上。因此，穿袜子是最好的选择。由于袜子相对较薄，是否穿袜子都不会影响热曲线的趋势。在测试过程中，实际环境温度和测试时间分别通过温度计和秒表获得。

为了减少实验过程中由于振动等因素引起的噪音，将热像仪固定在三脚架上。热成像焦平面阵列的大小为640×480（对应于相机的空间分辨率），像素间距为17μ米 热像仪通过网络电缆与计算机通信。最终，收集到的热学视频将发送到MATLAB R2018b（美国马萨诸塞州内蒂克，Mathworks，Inc.）进行进一步分析。

• 热序数据的预处理

首先对热敏录像进行灰度处理。随后，我们在左脚后的第一帧的每个足迹中选择一个特定的正方形区域，并通过以下公式计算该区域中的平均像素值，从而获得一维热足迹信号。然后，根据帧和时间之间的关系将帧的变化映射到时间的变化。

其中s（i，j，x）是像素（i，j）和视频帧x 处热图像的像素强度；N是感兴趣区域（ROI）中像素坐标的向量，n是其数量。

 

•  Thermalfoot模型

可以通过简单的图像处理操作轻松提取反映脚与地面之间的温差的原始温度曲线。但是我们的研究高于提取温度差曲线。

我们的研究面临两个挑战：

（1）找到可以描述温度曲线变化规律的通用模型。由于体重，在实际的实验过程中，我们可以观察到以下事实：将产生三种不同类型的曲线，这给我们建立热足模型带来了很多困难；

（2）在实际应用中，由于缺乏先验知识，我们只能使用有限的观测数据来拟合热足模型来进行出发时间反转。

• 指数下降期起点的确定

为了自动找出指数下降期的起点，使用了以下步骤。

为了减少随机噪声，仪器性能和环境温度的波动，我们对原始数据{Dk，k = 1,2，...，n}和相应的平滑曲线{D ^ k，k}使用数据平滑处理= 1,2，...，n}。平滑滤波器在消除突变点方面有局限性，这可能会影响曲线的总体趋势。为了消除这些突变点，采用了以下两个约束。

约束

（1）：通过分析大量曲线，我们发现两个相邻点之间的归一化亮度差将超过0.05。因此，可以通过确保当前时间点xk，i和后面的时间点xk，i + 1之间的亮度差不超过0.05，来滤除突变点。对于D ^ k中的任何时间点xk，i，温度值或像素强度应遵循以下关系。

|yk,i−yk,i+1|<0.05,i=1,2,...,Nk

其中，i是时间指数，Nk是第K个热曲线上的总点数。

第一个约束条件可以帮助我们消除大量的突变点。令通过约束

（1）获得的局部域中的点集的时间值集为A = {αk，i'，k = 1,2，...，n}，其中i'∈{1,2， ...，Nk}。随后，使用约束

（2）继续寻找指数下降期的起点。为避免获得局部下降点，我们将每个点与下一个100点的平均值进行比较：如果该点的亮度值大于或等于下一个100点的平均亮度值，则认为该曲线具有 此时呈下降趋势。约束（2）：使对应于时间点xk，i的温度值yk，i大于或等于下一个100点的平均温度，应满足以下关系。

详细公式流程推到可以参考底部论文。

 

• 出发点的确定

正如我们在图3中看到的那样，当对象离开时，热曲线上会出现一个突变点。像素强度或温度在突变点附近急剧变化。基于此特征，我们设计了一种算法，可以获取有关这种变化的信息。为了减少其他突变点（特别是下降期附近的点）的干扰，我们仅分析指数下降期开始点之前的点

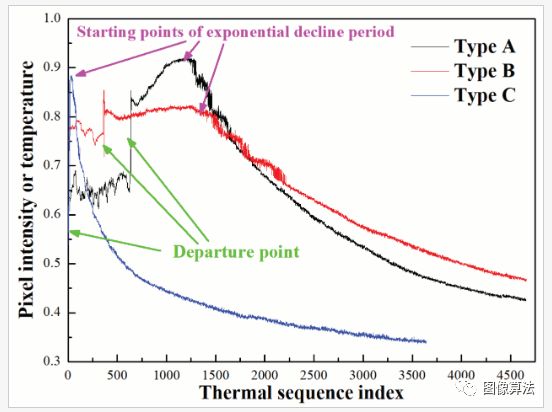
图3. 从原始热学视频中提取的三个典型热学曲线

• 热足迹模型的建立

对象离开地板后，对象站立的温度高于大气温度。根据牛顿的冷却定律，测试仪所在地板的表面温度开始下降，并且变化率与表面温度和稳定温度之间的差成比例。

 

• 热足迹模型评估

使用以下方程式评估热足模型的拟合优度：我们认为xN为一组原始温度样本数据{x1，x2，…，xN}的平均值。根据热足模型，我们获得了新的温度样本数据{y1，y2，…，yN}，其平均值为yN。我们计算相关系数r：

 

结果

• 热序曲线的定性分析

彻底分析所有获得的曲线后，我们将它们分为三种类型（图3）：

A型（缓慢上升）：当人的脚离开地面时，曲线缓慢上升到最高点，然后呈指数下降，最终达到稳定状态。

B型（固定）：当人的脚离开地面时，曲线保持极微起伏的状态，直到曲线呈指数下降，最终达到稳定状态。

C型（急剧上升）：当人的脚离开地面时，曲线急剧而迅速地上升到峰值，然后立即呈指数下降，最终达到稳定状态。

我们将人脚离开地面的时间定义为出发点。具体而言，对于类型A和C，将像素强度最高的点定义为指数下降周期的起点。

基于上述曲线的不同特征，我们分析了它们在指数下降期的起点和起点之间表现出三种不同状态的原因。

A型（缓慢上升）：我们怀疑人的脚离开地面时会向地面施加力，导致地面热量上升，从而导致弯道缓慢上升。此外，传感器延迟（即传感器切换可能会滞后于实际图像切换）也会在左脚离开后导致曲线上的缓慢上升过程。

B型（固定）：脚离开地面后，曲线略微波动，然后根据牛顿冷却定律，呈指数下降，最终达到稳定状态。这是一条理想的曲线。

C型（急剧上升）：我们假设测量时间短和像素急剧变化，使得脚离开地面后曲线急剧上升。

 

根据牛顿的冷却定律，地面温度会不断散失热量。每个曲线在一个时间点之后将呈现指数下降的趋势，并最终达到稳定状态（即与环境温度基本相同）。

• 滞后时间和指数下降期起点的统计分析

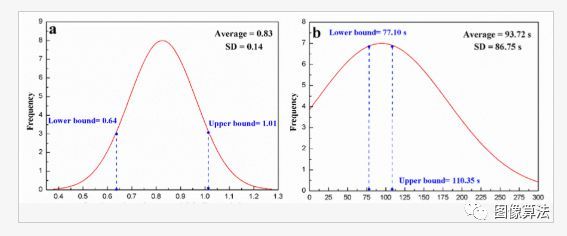
我们获得了107组起点和滞后时间。对于起点（图 4a ）和滞后时间（图 4b），归一化统计指标（平均值，±标准偏差）分别为0.83，±0.14和93.72 s，±86.75 s 。在95％置信区间下，分别选择[0.64，1.01]和[77.10 s，110.35 s]作为环境温度从16到16的起始点和滞后时间的估计范围。∘C到28 ∘C.这两个估计的间隔将用于后续的出发时间估计。

转存失败重新上传取消

图4.我们数据集中 指数下降期（a）和滞后时间（b）的起点的正态分布。

• 模型拟合的性能分析

Thermalfoot模型拟合的性能

我们使用一组原始数据（从起点到稳态）构建了热足模型，拟合结果如图5所示。根据热足模型的物理意义，在解析表达式中，指数下降期起点与稳态温度之差为0.3748。x之前的系数由牛顿冷却定律确定；稳态温度值为0.3628。请注意，所有温度值均已标准化。原始温度值与拟合温度值之间的相关系数为0.9986，表明所获得的热压脚模型可以基本反映原始数据的变化。数据集中其他曲线的拟合结果也令人满意。

图5. 使用牛顿冷却定律的指数下降阶段的一种典型拟合结果。

• 出发时间估计

考虑了两种情况用于出发时间估计的残差分析：

（1）通过热足迹模型估算的起点：在这种情况下，我们假设从指数下降期的起点到稳态的所有数据都是已知的，并已用于建模。地面真相的离开时间是通过Thermalfoot模型估算的。随后，对于每个热曲线，从四个不同的捕获时间点viz得出四个估计的离开时间。使用热压脚模型获得了三分之一，一半，三分之二和四分之三。进行残留分析以评估热压脚模型的性能（图6）。我们将残值超过350 s的数据点视为离群值，并在进行残差图时排除这些数据。总共消除了15分。如图6所示，我们可以观察到几乎所有残差都随机散布在完美估计线附近（残差= 0 s），并且位于250 s的上边界线和-250 s的下边界线内，这表明热压脚模型的性能是满意的。捕获时间分别为三分之一，二分之一，三分之二和四分之三，出发时间的标准偏差分别为55.02 s，64.00 s，65.68 s和83.29 s。这表明随着可使用信息的减少，模型的性能也会降低。

图6. 在通过热足迹模型估算的地面真相离开时间的情况下，不同点（N = 92）的离开时间的残差：（a）三分之一点，（b）一半点，（c）三分之二的点，和（d）四分之三的点。（总共消除了15个具有较大偏差（> 350 s）的点）。

 

在这种情况下，存在一个严重的问题，即基于所有数据建立了热足模型，但是，在实际应用中，捕获时间点之前的数据是未知的。情况二满足实际应用条件。

（2）通过统计分析估算的起点：在这种情况下，我们假设指数下降期的起点遵循高斯分布，并在一定的环境温度下在某个区域内波动。因此，将从拟合的高斯分布中得出的平均值用于建模。真正的出发时间由秒表记录。然后，根据每个热曲线，从四个不同的捕获时间点viz得出四个估计的离开时间。使用热压脚模型获得了三分之一，一半，三分之二和四分之三。进行残差分析以评估热压脚模型的性能（图7）。

我们将值大于550 s的残差点视为离群值。制作残差图时，总共消除了30个离群值。我们可以从图7中观察到就是说，几乎所有残差都随机散布在完美估计线附近（残差= 0 s），并且位于+500 s的上边界线和-500 s的下边界线内。考虑到情况2比情况1更实际，热脚模型的性能不如情况1令人满意，但仍被接受。出发时间的标准偏差为129.06 s，184.81 s，177.34 s和222.81。分别为s的三分之一，一半，三分之二和四分之三的捕获时间。这也表明，模型的性能会随着我们可以利用的信息的减少而降低。

图7. 在通过统计分析估计指数下降期的起点的情况下，不同时间点（N = 77）的出发时间剩余时间：（a）三分之一点，（b）一半点，（c）的三分之二，（d）的四分之三。（消除了总共30个具有较大偏差（> 515 s）的点）。

 

• 在不同捕获时间点估计出发时间的准确性

使用热脚模型计算在不同捕获时间点（三分之一点，一半点，三分之二点，四分之三点，四分之五点和五分之六点）的估计出发时间的准确性（图8）。随着曲线趋于稳定状态，热脚模型估计出发时间的准确性从71.96％降低到11.21％。这种现象表明，对于每个热压脚模型，都必须有一个故障点。Thermalfoot模型将无法推断出故障点之后的捕获时间点的起飞时间。

 

• 与主观计算方法的比较

为了衡量使用热脚模型估计出发时间的有效性，我们将热脚模型的计算方法与两种主观计算方法进行了比较，获得了表1中的结果。通过三种方法获得的精度显示出相同的模式，即，随着我们从热压脚曲线获得的信息减少，精度降低。如表1所示，主观计算2 胜过主观计算1个。但是，随着我们可以使用的信息减少，这两种方法之间的差异变得很小。就三个不同的捕获时间点（分别为三分之一，一半和三分之二）而言，热敏脚计算所获得的精度均高于两种主观计算方法所获得的精度。关于其他捕获时间点。在三分之四，四分之五和五分之六的情况下，这三种方法获得的精度相对接近。当我们选择的曲线接近指数下降期的起点时，通过热压脚模型计算获得的准确性相对较高（精度分别为71.96％，50.47％和42.06％，分别为三分之一，二分之一和三分之二，分别。）。主观计算2当我们选择的曲线接近稳态时，热脚模型计算具有相似的结果，其中本地信息对于我们估计总体趋势而言太少了。因此，证明了热足模型在实际应用中是有效的。

表1. 与两种主观计算方法的比较。（主观计算1个 和主观计算2 指出专家分别不使用和使用辅助工具，例如标尺。）

表1. 与两种主观计算方法的比较。（主观计算 1个  和主观计算 2  指出专家分别不使用和使用辅助工具，例如标尺。）

 

在实践中，如果我们可以在短时间内获得热脚信息，则可以利用热脚模型来估计起飞时间。如果我们无法获得换句话说，如果我们获得的热足信息不足以仅使用热足模型来解决问题，那么我们可以尝试使用辅助手段（例如标尺）在以下基础上进行主观计算：热足模型计算。根据我们的实验，只有这样做，我们才能获得更令人满意的结果。尽管目击者可能知道肇事者刚离开不久，但他或她可能无法知道更具体和准确的出发时间。可以说，主观的计算是由参加研究的人完成的，在某些方面，他们比其他人更专业。因此，热足模型的计算方法要好于证人的主观计算。在实际条件下应用我们的方法是有效的。

 

讨论

离群值用引号引起来，因为它是由模型反推的失败而不是仪器测量错误引起的。我们知道滞后时间的计算和起点的选择会影响模型估计的结果。因此，如何确定滞后时间和指数下降期起始点的值，是利用热足模型反演出发时间的最大挑战。滞后时间表示从人脚离开地板到热曲线的时间开始减少。指数下降期的起点是指热脚曲线开始下降的点。在实际应用中，没有其他技术的帮助，我们无法直接获得这两个参数的值。为了解决这个问题，我们假设在一定温度范围内，滞后时间和指数下降期的起点遵循正态分布，并且它们的值都在一定区域内波动。

 

因此，我们进行了以下分析。在上述假设的情况下，模型的后推结果无疑会有很多错误。根据已知的起点，本研究中删除了15个异常数据，其余92个数据用于残差分析。基于预测的起点，我们删除了30个异常数据，并将其余的77个数据用于残差分析。15个来自预测点的情况的异常数据中包括在已知起点情况下发生的异常数据。表2显示了两种情况的异常值比率：环境温度为16时的已知起点和预测起点∘C和28 ∘C.我们发现，如果已知起点，则在两个温度下的异常值比率基本相同（14.29％对13.38％）。但是，在预测起点的情况下，离群比为16∘C低于28 ∘C（26.29％对29.23％）。可能是因为更多的环境温度接近了健康人脚的平均温度（27-30∘C）[ 36 ]，热曲线达到稳定状态的速度越快。基于此，建立热脚模型的先验知识较少，从而导致更多的异常值。

 

表2. 两种情况的异常值比率：环境温度为16°C和28°C时的已知起点和预测起点。

 

ROI选择的讨论

在这项研究中，在预处理过程中随机选择了ROI，我们发现曲线的形状受脚底内不同区域和ROI大小不同的影响很大，如图9所示。

 

 

图9. ROI选择对热曲线生成的影响：（a）脚掌可能选择ROI；（b）从不同的ROI中提取的热曲线；（c）从不同大小的相同ROI提取的热曲线。（像素值已标准化）

ROI的选择对热曲线的影响：当ROI的大小相同但位置不同时（例如，图9中Middle1，Middle2，Middle3和Middle4的四个区域），通过比较四个曲线，我们发现不同部分的最高温度值之间存在差异。在以相同大小提取的四个RIO中，代表大脚趾根部的区域（即Middle4）显示出最高温度。同时，在热足模式中，脚的前底的温度高于脚的后跟的温度，并且在足弓区域可能发生较低的温度。它与先前文献的结果不一致。现有文献表明，脚中部（即足弓区域）的温度应高于脚上其他区域。我们认为可能是由于与地面的不完全接触导致了脚底温度分布的差异。由于在脚和地面之间会形成一个气隙，因此，热辐射和热对流将取代热传导，成为主要的传热方法，从而导致传热能力降低。因此，足弓区域的温度低于其他区域。

此外，这四个曲线的噪声之间的差异很小。通过比较曲线的体面部分，我们发现通过不同的ROI获得的曲线上体面部分的斜率是不一致的。我们推测，所选区域的初始温度和体面曲线的斜率可能在某种程度上呈正相关。

ROI大小对热曲线的影响：当所选ROI的位置相似但大小不同时（例如，图9中的三个中，小，大三个区域），比较曲线，则很明显可以看到，中部3和大区域的曲线基本上是一致的，但是小区域的温度值总体上较低，噪声更明显。通过图形化其他附加数据（未显示数据）进行验证，我们怀疑所选区域的大小与噪声之间存在某种程度的负相关关系，这意味着所选区域越小，其噪声就越大。

通常，尽管各条曲线之间存在差异，但曲线的总体趋势几乎相同。六个曲线的出发点集中在175 s到200 s的时间间隔中，指数下降期的起点也集中在325 s到375 s的时间间隔中。

• 背景辐射的影响

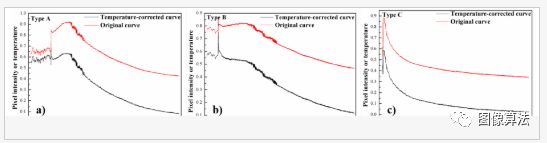
我们考虑了背景辐射对热压脚曲线的影响，图10显示了AC型的温度校正曲线。如图10所示，我们可以观察到温度校正曲线的趋势与原始曲线的趋势相似。结果，我们可以忽略地板的热辐射的影响。另外，热足迹的大气温度是恒定的，我们认为是否考虑大气温度没有区别。

图10. 三个原始热曲线及其温度校正曲线：（a – c）分别为A–C类型。

• 捕获时间点的影响

根据以上分析，热曲线最初随时间呈指数下降，在经过一定的热交换（包括热传导，热对流和热辐射）后逐渐趋于稳定。

 

我们发现，每条曲线在稳定状态下的温度不是一个确定的值，该温度保持接近但不等于环境温度。一般情况下，指数下降期的起点越高，稳定状态的温度值越高。而且，捕获时间点越接近稳态，出发时间的推论就越不准确。这是理所当然的：捕获时间点越接近稳定状态，用于建模的先验知识越少，模型的性能就越差。在这个研究中，我们认为捕获时间点的准确度低于15％是不可接受的，因此异常点可被视为确定模型实用性的故障点。

 

在实践中，如果所获得的温度在故障点之后，这是由时间窗口过长造成的，则很难反演站立的人的离开时间。因此，我们应采取措施减少这一长时间窗口的不利影响。我们建议证人或受害者在看到房屋内发生偷窃或其他犯罪时，应保持冷静。警察收集热压脚印信息的最佳时间是尽快，因此目击者应立即报警。另外，建议他们保持场景完整，以确保残留在地面上的热压脚印信息的完整性。警察到达时证人或被害人应简要说明警方可以使用的有效信息，并与警方合作收集热脚印信息，以帮助解决案件。相反地，估计犯罪者的离开时间范围的可能性在于获得警方在15分钟内在犯罪现场留在地面上的热脚印。随着技术的发展，我们希望热敏足印技术不局限于通过检测地面上剩余的热痕迹来推断时间点，而是可以利用相似的原理激发更多新颖的想法，以获取更有效的信息，从而建立更安全的社会环境。

• 站立时间的影响

在实际应用中，施暴者的站立时间是不确定的。我们的初步实验结果表明，静置时间对热曲线的趋势影响很小：在30 s和3分钟的静置时间内，热曲线的趋势基本相同。因此，尽管有些对象只是站立了很短的时间，但留在地板上的热脚曲线仍然可以为我们提供有用的建模信息，从而估算出出发时间。

 

结论

总之可以基于热迹线开发热足模型，以估计起飞时间。根据牛顿的冷却定律，能够使用似然函数来开发热足模型，并且这些模型的相关系数基本上都高于0.99，这表明我们的算法具有出色的拟合优度。在验证实验中，估计的出发时间点与地面真相时间之间的残差几乎在-500 s至500 s的范围内。

 

为了进一步评估热脚模型在实际应用中的出发时间反转的性能，计算模型的反转精度以确定反转时间是否在可接受的时间间隔内。热脚模型的反向精度，用于估计起飞时间的三分之一，二分之一，捕获时间点的三分之二，四分之三，四分之五和五分之六分别为71.96％，50.47％，42.06％，31.78％，21.70％和11.21％。两种主观评价方法的比较实验结果进一步证明了热足模型对出发时间反转的有效性。在有人离开后的短时间窗口中，热脚模型在出发时间反转上具有出色的性能，而在有人离开后的长时间窗口中，使用热脚模型准确确定出发时间可能只有大约15％。热足模型可以在一定程度上帮助警察解决犯罪，从而为人们的健康生活和社会保障与稳定提供更多保障。未来的工作可以集中在离群值，ROI选择，ROI大小和热脚模型在起飞时间反转时的性能上的不同捕获时间点。另外，我们可以探索在环境温度低于16°C的条件下热足模型的性能。

 

论文地址：

https://res.mdpi.com/d_attachment/sensors/sensors-20-00782/article_deploy/sensors-20-00782-v2.pdf

更多论文地址源码地址：关注“图像算法”微信公众号