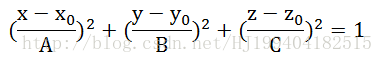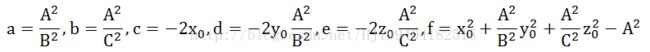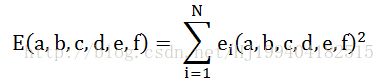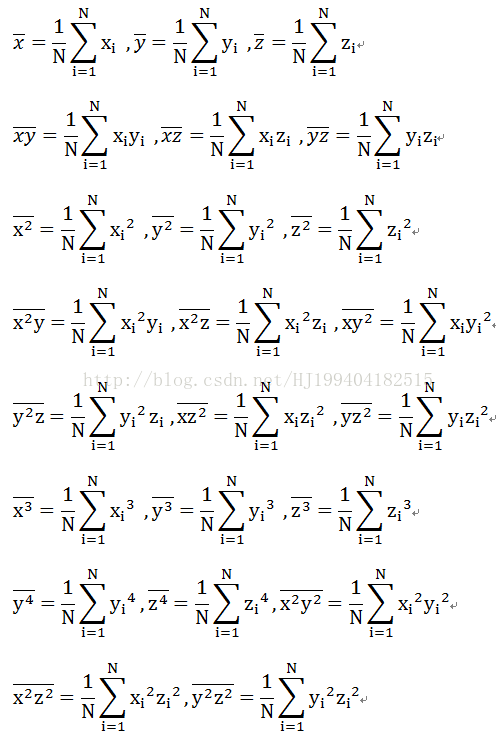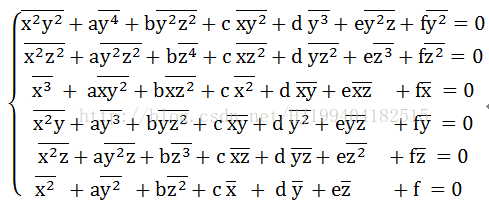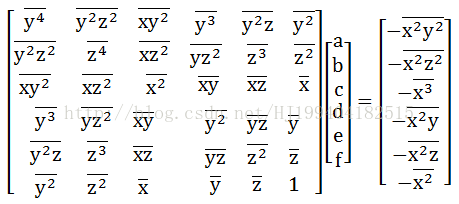空间二次曲面数据拟合算法推导及仿真分析
在上一篇的博客球面数据拟合算法简介中,笔者详细介绍了关于空间球面数据拟合的算法公式推导并给出了相应的Matlab代码及其仿真分析。本次笔者将上面这一情况进行更一般的推广,即取消了球面数据这一限制,数据可以是椭球面形式的,也就是说是任意的空间二次曲面形式的,可见球面的数据是它的一个特例。下面给出的是空间二次曲面的标准表达式:
一共有6个未知的参数,x0, y0, z0, A, B, C。写成一般式如下所示:
其中
对于有N个三维椭球面样本对其进行椭球面拟合,我们只需要对参数a,b,c,d,e,f进行估计,从而就可以得到x0, y0, z0, A, B, C。那么怎么利用样本去估计这些参数呢?这实际上就是模型参数估计的内容,模型参数估计有很多种方法,其中最基本的方法就是最小二乘法(Least Squares Method),这个在上一篇《球面数据拟合算法简介》博客中有用到。由于它的原理直观,算法简单,收敛性能好,且不要求先验的统计知识,因而被广泛应用。最小二乘法是在1795年由大数学家高斯(C.F.Gauss)研究天体运动轨道问题提出的,它的基本原理是实际观测值与模型计算值的误差的平方和最小原理,由此而得名“最小二乘”法。应该注意的是最小二乘法是一种思想,由它衍生出来的公式可以有很多种。本次的空间二次数据拟合算法的推导利用的也是最小二乘法,不同的是本次是先估计参数a,b,c,d,e,f,然后间接的得到参数x0, y0, z0, A, B, C,这样做给公式推导带来了很大的方便,而且结果与直接推导的完全一样。
基于最小二乘的拟合方法公式推导
下面来利用最小二乘的思想进行推导,首先对于每个样本点(x_i,y_i,z_i),其误差可表示为:
![]()
则误差平方和为:
我们令E对于a,b,c,d,e,f的各一阶偏导数等于0,则有:
令:
带入化简得:
写成矩阵的形式有:
求解该六元一次方程组即可得到a,b,c,d,e,f的估计值。进而得到x0, y0, z0, A, B, C。
Matlab代码分析与仿真
代码主要有两个部分,第一部分是生成带噪声的椭球面数据,第二部分是利用上述推导的算法来估计相关的参数,下面给出相关的代码
clear all;
close all
clc;
A = 300; % x方向上的轴半径
B = 400; % y方向上的轴半径
C = 500; % z方向上的轴半径
x0 = -120; %椭球球心x坐标
y0 = -67; %椭球球心y坐标
z0 = 406; %椭球球心z坐标
SNR = 30; %信噪比
%********************************生成随机椭球球面数据************************************
%利用在球坐标系下的参数方程来生成各个椭球的样本点
num_alfa = 100;
num_sita = 50;
alfa = (0:num_alfa-1)*1*pi/num_alfa;
sita = (0:num_sita-1)*2*pi/num_sita;
x = zeros(num_alfa,num_sita);
y = zeros(num_alfa,num_sita);
z = zeros(num_alfa,num_sita);
for i = 1:num_alfa
for j = 1:num_sita
x(i,j) = x0 + A*sin(alfa(i))*cos(sita(j));
y(i,j) = y0 + B*sin(alfa(i))*sin(sita(j));
z(i,j) = z0 + C*cos(alfa(i));
end
end
x = reshape(x,num_alfa*num_sita,1); %转换成一维的数组便于后续的处理
y = reshape(y,num_alfa*num_sita,1);
z = reshape(z,num_alfa*num_sita,1);
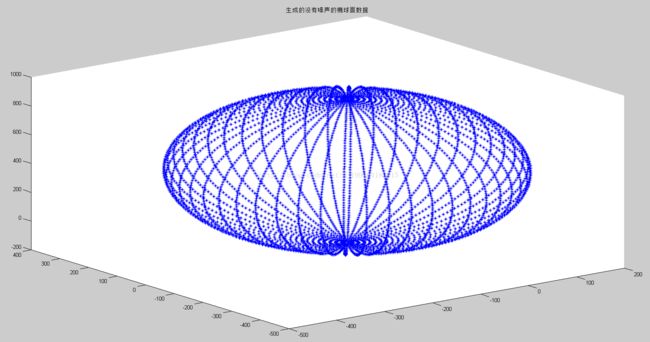
figure;
plot3(x,y,z,'*');
title('生成的没有噪声的椭球面数据');
%加入均值为0的高斯分布噪声
amp = 10^(-SNR/20)*A;
x = x + amp*rand(num_alfa*num_sita,1);
y = y + amp*B/A*rand(num_alfa*num_sita,1);
z = z + amp*C/A*rand(num_alfa*num_sita,1);
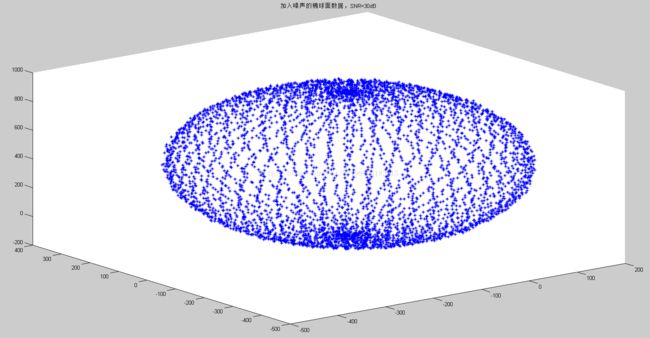
figure;
plot3(x,y,z,'*');
string = ['加入噪声的椭球面数据,SNR=',num2str(SNR),'dB'];
title(string);
%*******************************************************************************************
%空间二次曲面拟合算法
num_points = length(x);
%一次项统计平均
x_avr = sum(x)/num_points;
y_avr = sum(y)/num_points;
z_avr = sum(z)/num_points;
%二次项统计平均
xx_avr = sum(x.*x)/num_points;
yy_avr = sum(y.*y)/num_points;
zz_avr = sum(z.*z)/num_points;
xy_avr = sum(x.*y)/num_points;
xz_avr = sum(x.*z)/num_points;
yz_avr = sum(y.*z)/num_points;
%三次项统计平均
xxx_avr = sum(x.*x.*x)/num_points;
xxy_avr = sum(x.*x.*y)/num_points;
xxz_avr = sum(x.*x.*z)/num_points;
xyy_avr = sum(x.*y.*y)/num_points;
xzz_avr = sum(x.*z.*z)/num_points;
yyy_avr = sum(y.*y.*y)/num_points;
yyz_avr = sum(y.*y.*z)/num_points;
yzz_avr = sum(y.*z.*z)/num_points;
zzz_avr = sum(z.*z.*z)/num_points;
%四次项统计平均
yyyy_avr = sum(y.*y.*y.*y)/num_points;
zzzz_avr = sum(z.*z.*z.*z)/num_points;
xxyy_avr = sum(x.*x.*y.*y)/num_points;
xxzz_avr = sum(x.*x.*z.*z)/num_points;
yyzz_avr = sum(y.*y.*z.*z)/num_points;
%计算求解线性方程的系数矩阵
A0 = [yyyy_avr yyzz_avr xyy_avr yyy_avr yyz_avr yy_avr;
yyzz_avr zzzz_avr xzz_avr yzz_avr zzz_avr zz_avr;
xyy_avr xzz_avr xx_avr xy_avr xz_avr x_avr;
yyy_avr yzz_avr xy_avr yy_avr yz_avr y_avr;
yyz_avr zzz_avr xz_avr yz_avr zz_avr z_avr;
yy_avr zz_avr x_avr y_avr z_avr 1;];
%计算非齐次项
b = [-xxyy_avr;
-xxzz_avr;
-xxx_avr;
-xxy_avr;
-xxz_avr;
-xx_avr];
resoult = inv(A0)*b;
%resoult = solution_equations_n_yuan(A0,b);
x00 = -resoult(3)/2; %拟合出的x坐标
y00 = -resoult(4)/(2*resoult(1)); %拟合出的y坐标
z00 = -resoult(5)/(2*resoult(2)); %拟合出的z坐标
AA = sqrt(x00*x00 + resoult(1)*y00*y00 + resoult(2)*z00*z00 - resoult(6)); % 拟合出的x方向上的轴半径
BB = AA/sqrt(resoult(1)); % 拟合出的y方向上的轴半径
CC = AA/sqrt(resoult(2)); % 拟合出的z方向上的轴半径
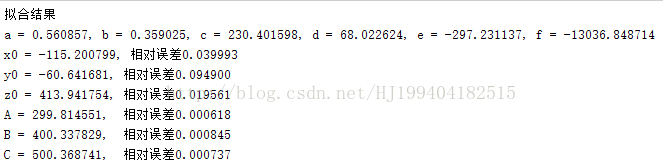
fprintf('拟合结果\n');
fprintf('a = %f, b = %f, c = %f, d = %f, e = %f, f = %f\n',resoult);
fprintf('x0 = %f, 相对误差%f\n',x00,abs((x00-x0)/x0));
fprintf('y0 = %f, 相对误差%f\n',y00,abs((y00-y0)/y0));
fprintf('z0 = %f, 相对误差%f\n',z00,abs((z00-z0)/z0));
fprintf('A = %f, 相对误差%f\n',AA,abs((A-AA)/A));
fprintf('B = %f, 相对误差%f\n',BB,abs((B-BB)/B));
fprintf('C = %f, 相对误差%f\n',CC,abs((C-CC)/C));可以看到拟合的误差很小,同时我们也可以看到拟合后的参数A,B,C的相对误差比x0,y0,z0要小。
结束语
从matlab的仿真分析验证了前面的公式推导的正确性,关于空间二次曲面拟合的运用,一个最典型的应用就是对地磁计静态校准的应用,地磁计在没有校准的情况下如果让其在空间的各个卦限旋转一遍得到输出数据的轨迹就是个椭球面,利用该算法就可以有效的估计出静态干扰以及每个轴的相对灵敏度。还有就是在图像处理、机器人等领域,需要对运动图像中的椭圆曲线进行快速检测,实际上这个时候拟合的是一个椭圆曲线,可以使用上述类似的方法来进行拟合,它的参数要少一些,更为简单,有兴趣的读者可以自己尝试推导并用matlab仿真验证一下。