虫食算-详解-noip2004-深搜
虫食算 网址:https://vijos.org/p/1099
描述
所谓虫食算,就是原先的算式中有一部分被虫子啃掉了,需要我们根据剩下的数字来判定被啃掉的字母。来看一个简单的例子:
43#9865#045
+ 8468#6633
= 44445506678
其中#号代表被虫子啃掉的数字。根据算式,我们很容易判断:第一行的两个数字分别是5和3,第二行的数字是5。
现在,我们对问题做两个限制:
首先,我们只考虑加法的虫食算。这里的加法是N进制加法,算式中三个数都有N位,允许有前导的0。
其次,虫子把所有的数都啃光了,我们只知道哪些数字是相同的,我们将相同的数字用相同的字母表示,不同的数字用不同的字母表示。如果这个算式是N进制的,我们就取英文字母表午的前N个大写字母来表示这个算式中的0到N-1这N个不同的数字:但是这N个字母并不一定顺序地代表0到N-1)。输入数据保证N个字母分别至少出现一次。
BADC
+ CRDA
= DCCC
上面的算式是一个4进制的算式。很显然,我们只要让ABCD分别代表0123,便可以让这个式子成立了。你的任务是,对于给定的N进制加法算式,求出N个不同的字母分别代表的数字,使得该加法算式成立。输入数据保证有且仅有一组解
格式
输入格式
输入包含4行。第一行有一个正整数N(N<=26),后面的3行每行有一个由大写字母组成的字符串,分别代表两个加数以及和。这3个字符串左右两端都没有空格,从高位到低位,并且恰好有N位。
输出格式
输出包含一行。在这一行中,应当包含唯一的那组解。解是这样表示的:输出N个数字,分别表示A,B,C……所代表的数字,相邻的两个数字用一个空格隔开,不能有多余的空格。
样例1
样例输入1[复制]
5 ABCED BDACE EBBAA
样例输出1[复制]
1 0 3 4 2
限制
每个测试点1s
---------------------------------------------------------------
题目解析
首先想到的就是暴力枚举,其实也就是搜索了,对应的填数
解结构是0.1..n-1的排列(0,1,2,3,4) (0,1,2,4,3)....情况为n*n-1*n-2*..*1 = n!时间复杂度太高,显然超时
必须要优化剪枝
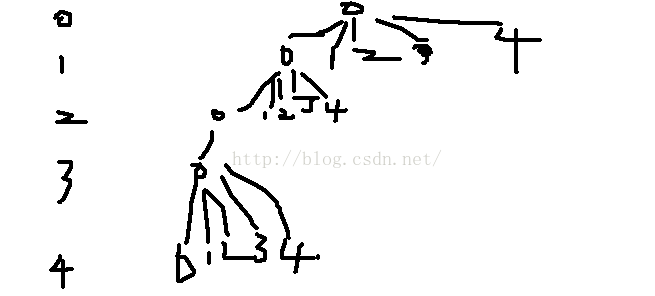
刻画下解空间树:
之所以没有第1层表示 第1个字母取0.1.2.3.4 第2层表示第2个字母取0.1.2.3.4 点不能重复取区分开来,是为了程序的循环书写便利,只需要加个use[26]标志位即可区分
关键点:
1、已使用过得数字不得重复用
2、如果已找到唯一的可行解,那么后面就不需要再搜索 这个是一个关键信息点:可以影响到4个点的值
3、进入每一层的时候,剪枝看当前已经取数的点,可行性
剪枝策略:
1、对于每一列 a+b=c ,只有2种运算 无低位进位 a+b=c 有低位进位a+b+1=c
不必要讨论这一列如果在最低位,根本不会有进位,等等这些,因为我们只是 在正确的情况下 “粗略”剪枝
如果已知a,b,c 三字母都已填数 那么 判断(a+b)%n=c (a+b+1)%n=c都不成立,那这个肯定不对
这一个条件可以过3个点
2、如果已知a,b,c三者其中2个
如a,b 已知 c1 = (a+b)%n c2=(a+b+1)%n 如果这c1,c2两个数都被占用了,那肯定不可行
如a,c 已知则b1=(c-a+n)%n b2=(c-a-1+n)%n 如果这b1,b2两个数都被占用了,那肯定不行
如b,c 已知则a1=(c-b+n)%n a2=(c-b-1+n)%n 如果这a1,a2两个数都被占用了,那肯定不行
加上这个条件可以多过一个点,过4个点
3、加上关键点2 可以过6个点
4、在代码里把 剪枝函数放在dfs前面可以凑巧过1个点,但这个不是必须的,只是恰好对应了测试数据
这样过了7个点,详细代码如下:
//#include
#include
#include
#include
#include
#include
using namespace std;
int n;//读入几进制0.1.2.3...n-1
int res[26];//保存A.B..Z代表的数字
int used[26];//保存这个对应数字是否被用,因为题目说每个字母只能代表一个数
string a,b,c;//保存加数1,加数2,和
int flag = 0;//是否已找到符合条件的唯一解//加上这个多对了2个点
//剪枝优化函数,来判断当前的字母的数字取法是否可行
//题目就是一个可行与否的问题
int Check()
{
int i;
//看是否满足 a+b==c
for (i=0;i<=n-1;i++)
{
char a1=a[i]-'A',b1=b[i]-'A',c1=c[i]-'A';//取三个数第i位置值
if(res[a1]!=-1 && res[b1]!=-1 && res[c1]!=-1)//3个数都知道
{
if( (res[a1]+res[b1])%n!=res[c1] &&//无进位
(res[a1]+res[b1]+1)%n!=res[c1])//有进位
return 0;
}
//加上后面这些多对了1个点
if(res[a1]!=-1 && res[b1]!=-1 && res[c1]==-1)//如果只知道其中2个
{
int sum1,sum2;//sum1无进位,sum2有进位
sum1 = (res[a1]+res[b1])%n;
sum2 = (res[a1]+res[b1]+1)%n;
if (used[sum1] && used[sum2])//可能填在c1的数都用了肯定不行
return 0;
}
if (res[a1]!=-1 && res[b1]==-1 && res[c1]!=-1)//和与一个加数知道
{
int js1,js2;//js1无进位,js2有进位
js1 = (res[c1]-res[a1]+n)%n;
js2 = (res[c1]-res[a1]-1+n)%n;
if (used[js1] && used[js2])//可能填写咋b1位置的数都被用了
return 0;
}
if (res[a1]==-1 && res[b1]!=-1 && res[c1]!=-1)//和与一个加数知道
{
int js1,js2;//js1无进位,js2有进位
js1 = (res[c1]-res[b1]+n)%n;
js2 = (res[c1]-res[b1]-1+n)%n;
if (used[js1] && used[js2])//可能填写咋b1位置的数都被用了
return 0;
}
}
return 1;
}
/*剪枝策略只这样写,数据只过3个点
int Check()
{
int i;
//看是否满足 a+b==c
for (i=0;i<=n-1;i++)
{
char a1=a[i]-'A',b1=b[i]-'A',c1=c[i]-'A';//取三个数第i位置值
if(res[a1]!=-1 && res[b1]!=-1 && res[c1]!=-1)
{
if( (res[a1]+res[b1])%n!=res[c1] &&//无进位
(res[a1]+res[b1]+1)%n!=res[c1])//有进位
return 0;
}
}
return 1;
}
*/
//严格判断当前所有字母的填数满足等式否
int OK()
{
int i;
int jinwei=0;
int jiahe;
for (i=n-1; i>=0; i--)
{
char a1=a[i]-'A',b1=b[i]-'A',c1=c[i]-'A';
jiahe = (res[a1]+res[b1]+jinwei)%n;//计算和
jinwei =( res[a1]+res[b1]+jinwei)/n;//计算进位
if (jiahe!=res[c1]) return 0;
}
if (jinwei>0) return 0;
return 1;
}
void dfs(int k)//深搜,利用系统的堆栈枚举
{
int i;
if (flag) return ;//已找到解
if (!Check()) return;//现在的方法不合理
if(k==n)//找到可行解且唯一(题目得知),输出
{
if (OK())//如果当前所有字母填数满足等式则输出
{
for(i=0; i<=n-2; i++) cout<>n;
cin>>a>>b>>c;
memset(res,-1,sizeof(res));
dfs(0);
//system("pause");
return 0;
} --------------------------------------------
后面怎么加条件都不行了
看题解发现:在写代码过程中是按照
A B C D E
0 1 2 3 4
0 1 2 4 3
按照字母顺序来遍历解空间的,在进行验证的时候 比如 当前指导 A 0 B 1 C2
验证的时候是按照从高位列向低位列验证也就是
判断 A + B = E 判断2:B+D=B 判断3:C+A=B 其实发现只有3才是能真正起到作用的一个
而且直观感受低位数一般可以较大些,可以进位,高位较小些,不进位所以
也就是没有“”优化“”的盲目枚举判断
题解上就给出了一种按照字母从右向左,从上向下出现的顺序来进行枚举搜索 样例为例:
最右上角为D->E->A->E>C>A>C>A>B>B>D>B>A>B>E
也就是提取下
D E A C B
4 3 2 1 0
4 3 2 0 1
按照这样来枚举,那么在验证的时候,也修改为从右侧低位列向左侧高位列验证,这样基本D 4 E 3 A 2的时候
D+E=A 这个验证策略就已经可以真正起作用,换句话说,就是可以在尽可能浅的层上,让剪枝策略今早的发挥作用,剪掉更过不需计算的分支
这样修改后,AC
0-------------------------
AC代码
测试数据 #0: Accepted, time = 0 ms, mem = 576 KiB, score = 10
测试数据 #1: Accepted, time = 0 ms, mem = 576 KiB, score = 10
测试数据 #2: Accepted, time = 0 ms, mem = 576 KiB, score = 10
测试数据 #3: Accepted, time = 0 ms, mem = 576 KiB, score = 10
测试数据 #4: Accepted, time = 0 ms, mem = 576 KiB, score = 10
测试数据 #5: Accepted, time = 0 ms, mem = 572 KiB, score = 10
测试数据 #6: Accepted, time = 15 ms, mem = 576 KiB, score = 10
测试数据 #7: Accepted, time = 0 ms, mem = 572 KiB, score = 10
测试数据 #8: Accepted, time = 31 ms, mem = 576 KiB, score = 10
测试数据 #9: Accepted, time = 15 ms, mem = 576 KiB, score = 10
Accepted, time = 61 ms, mem = 576 KiB, score = 100
/include
#include
#include
#include
#include
#include
using namespace std;
int n;//读入几进制0.1.2.3...n-1
int res[26];//保存A.B..Z代表的数字
int used[26];//保存这个对应数字是否被用,因为题目说每个字母只能代表一个数
string a,b,c;//保存加数1,加数2,和
int flag = 0;//是否已找到符合条件的唯一解//加上这个多对了2个点//
//-----最多只能7个点了,原先是从abcd..填字母,改变
char pos[26];//保存从右往左,从上往下的字母出现顺序,判断的时候也按这个顺序判断
int usedZiMu[26];//保存该字母是否已经出现
//剪枝优化函数,来判断当前的字母的数字取法是否可行
//题目就是一个可行与否的问题
int Check()
{
int i;
//看是否满足 a+b==c
for (i=n-1;i>=0;i--)
{
char a1=a[i]-'A',b1=b[i]-'A',c1=c[i]-'A';//取三个数第i位置值
if(res[a1]!=-1 && res[b1]!=-1 && res[c1]!=-1)//3个数都知道-----3个点
{
if( (res[a1]+res[b1])%n!=res[c1] &&//无进位
(res[a1]+res[b1]+1)%n!=res[c1])//有进位
return 0;
}
//加上后面这些多对了1个点
if(res[a1]!=-1 && res[b1]!=-1 && res[c1]==-1)//如果只知道其中2个
{
int sum1,sum2;//sum1无进位,sum2有进位
sum1 = (res[a1]+res[b1])%n;
sum2 = (res[a1]+res[b1]+1)%n;
if (used[sum1] && used[sum2])//可能填在c1的数都用了肯定不行
return 0;
}
if (res[a1]!=-1 && res[b1]==-1 && res[c1]!=-1)//和与一个加数知道
{
int js1,js2;//js1无进位,js2有进位
js1 = (res[c1]-res[a1]+n)%n;
js2 = (res[c1]-res[a1]-1+n)%n;
if (used[js1] && used[js2])//可能填写咋b1位置的数都被用了
return 0;
}
if (res[a1]==-1 && res[b1]!=-1 && res[c1]!=-1)//和与一个加数知道
{
int js1,js2;//js1无进位,js2有进位
js1 = (res[c1]-res[b1]+n)%n;
js2 = (res[c1]-res[b1]-1+n)%n;
if (used[js1] && used[js2])//可能填写咋b1位置的数都被用了
return 0;
}
}
return 1;
}
/*剪枝策略只这样写,数据只过3个点
int Check()
{
int i;
//看是否满足 a+b==c
for (i=0;i<=n-1;i++)
{
char a1=a[i]-'A',b1=b[i]-'A',c1=c[i]-'A';//取三个数第i位置值
if(res[a1]!=-1 && res[b1]!=-1 && res[c1]!=-1)
{
if( (res[a1]+res[b1])%n!=res[c1] &&//无进位
(res[a1]+res[b1]+1)%n!=res[c1])//有进位
return 0;
}
}
return 1;
}
*/
//严格判断当前所有字母的填数满足等式否
int OK()
{
int i;
int jinwei=0;
int jiahe;
for (i=n-1; i>=0; i--)
{
char a1=a[i]-'A',b1=b[i]-'A',c1=c[i]-'A';
jiahe = (res[a1]+res[b1]+jinwei)%n;//计算和
jinwei =( res[a1]+res[b1]+jinwei)/n;//计算进位
if (jiahe!=res[c1]) return 0;
}
if (jinwei>0) return 0;
return 1;
}
void dfs(int k)//深搜,利用系统的堆栈枚举
{
int i;
if (flag) return ;//已找到解
if (!Check()) return;//现在的方法不合理--从if (!used[i]&&Check())移到这里多了1个点共7个了
if(k==n)//找到可行解且唯一(题目得知),输出
{
if (OK())//如果当前所有字母填数满足等式则输出
{
for(i=0; i<=n-2; i++) cout<=0; i--)
{
//如果i还没被占用,且满足剪枝条件,则进行下层遍历
if (!used[i] )
{
used[i]=1;//i被占用
res[pos[k]]=i;//第k个字母取数字i
dfs(k+1);
used[i]=0;//i被释放,可以被其他字母占用
res[pos[k]]=-1;//第k个字母释放
}
}
return ;
}
int main()
{
int k=0,i;
//读入数据
cin>>n;
cin>>a>>b>>c;
memset(res,-1,sizeof(res));
memset(pos,-1,sizeof(pos));
//初始化
for (i=n-1; i>=0; i--)//从右向左
{
char a1=a[i]-'A',b1=b[i]-'A',c1=c[i]-'A';//全部转成对应数字下标
if (!usedZiMu[a1]) ///从上往下
{
usedZiMu[a1]=1;
pos[k++] = a1;
}
if (!usedZiMu[b1])
{
usedZiMu[b1]=1;
pos[k++] = b1;
}
if (!usedZiMu[c1])
{
usedZiMu[c1]=1;
pos[k++] = c1;
}
}
//for (i=0; i 测试数据 #0: Accepted, time = 0 ms, mem = 572 KiB, score = 10
测试数据 #1: Accepted, time = 0 ms, mem = 576 KiB, score = 10
测试数据 #2: Accepted, time = 0 ms, mem = 576 KiB, score = 10
测试数据 #3: Accepted, time = 0 ms, mem = 576 KiB, score = 10
测试数据 #4: Accepted, time = 0 ms, mem = 576 KiB, score = 10
测试数据 #5: Accepted, time = 0 ms, mem = 580 KiB, score = 10
测试数据 #6: Accepted, time = 62 ms, mem = 576 KiB, score = 10
测试数据 #7: Accepted, time = 15 ms, mem = 576 KiB, score = 10
测试数据 #8: Accepted, time = 265 ms, mem = 580 KiB, score = 10
测试数据 #9: Accepted, time = 0 ms, mem = 576 KiB, score = 10
Accepted, time = 342 ms, mem = 580 KiB, score = 100
//#include
#include
#include
#include
#include
#include
using namespace std;
int n;//读入几进制0.1.2.3...n-1
int res[26];//保存A.B..Z代表的数字
int used[26];//保存这个对应数字是否被用,因为题目说每个字母只能代表一个数
string a,b,c;//保存加数1,加数2,和
int flag = 0;//是否已找到符合条件的唯一解//加上这个多对了2个点//
//-----最多只能7个点了,原先是从abcd..填字母,改变
char pos[26];//保存从右往左,从上往下的字母出现顺序,判断的时候也按这个顺序判断
int usedZiMu[26];//保存该字母是否已经出现
//剪枝优化函数,来判断当前的字母的数字取法是否可行
//题目就是一个可行与否的问题
int Check()
{
int i;
//看是否满足 a+b==c
for (i=n-1;i>=0;i--)
{
char a1=a[i]-'A',b1=b[i]-'A',c1=c[i]-'A';//取三个数第i位置值
if(res[a1]!=-1 && res[b1]!=-1 && res[c1]!=-1)//3个数都知道-----3个点
{
if( (res[a1]+res[b1])%n!=res[c1] &&//无进位
(res[a1]+res[b1]+1)%n!=res[c1])//有进位
return 0;
}
//加上后面这些多对了1个点
if(res[a1]!=-1 && res[b1]!=-1 && res[c1]==-1)//如果只知道其中2个
{
int sum1,sum2;//sum1无进位,sum2有进位
sum1 = (res[a1]+res[b1])%n;
sum2 = (res[a1]+res[b1]+1)%n;
if (used[sum1] && used[sum2])//可能填在c1的数都用了肯定不行
return 0;
}
if (res[a1]!=-1 && res[b1]==-1 && res[c1]!=-1)//和与一个加数知道
{
int js1,js2;//js1无进位,js2有进位
js1 = (res[c1]-res[a1]+n)%n;
js2 = (res[c1]-res[a1]-1+n)%n;
if (used[js1] && used[js2])//可能填写咋b1位置的数都被用了
return 0;
}
if (res[a1]==-1 && res[b1]!=-1 && res[c1]!=-1)//和与一个加数知道
{
int js1,js2;//js1无进位,js2有进位
js1 = (res[c1]-res[b1]+n)%n;
js2 = (res[c1]-res[b1]-1+n)%n;
if (used[js1] && used[js2])//可能填写咋b1位置的数都被用了
return 0;
}
}
return 1;
}
/*剪枝策略只这样写,数据只过3个点
int Check()
{
int i;
//看是否满足 a+b==c
for (i=0;i<=n-1;i++)
{
char a1=a[i]-'A',b1=b[i]-'A',c1=c[i]-'A';//取三个数第i位置值
if(res[a1]!=-1 && res[b1]!=-1 && res[c1]!=-1)
{
if( (res[a1]+res[b1])%n!=res[c1] &&//无进位
(res[a1]+res[b1]+1)%n!=res[c1])//有进位
return 0;
}
}
return 1;
}
*/
//严格判断当前所有字母的填数满足等式否
int OK()
{
int i;
int jinwei=0;
int jiahe;
for (i=n-1; i>=0; i--)
{
char a1=a[i]-'A',b1=b[i]-'A',c1=c[i]-'A';
jiahe = (res[a1]+res[b1]+jinwei)%n;//计算和
jinwei =( res[a1]+res[b1]+jinwei)/n;//计算进位
if (jiahe!=res[c1]) return 0;
}
if (jinwei>0) return 0;
return 1;
}
void dfs(int k)//深搜,利用系统的堆栈枚举
{
int i;
if (flag) return ;//已找到解
//if (!Check()) return;//现在的方法不合理--从if (!used[i]&&Check())移到这里多了1个点共7个了
if(k==n)//找到可行解且唯一(题目得知),输出
{
if (OK())//如果当前所有字母填数满足等式则输出
{
for(i=0; i<=n-2; i++) cout<=0; i--)
{
//如果i还没被占用,且满足剪枝条件,则进行下层遍历
if (!used[i]&&Check() )
{
used[i]=1;//i被占用
res[pos[k]]=i;//第k个字母取数字i
dfs(k+1);
used[i]=0;//i被释放,可以被其他字母占用
res[pos[k]]=-1;//第k个字母释放
}
}
return ;
}
int main()
{
int k=0,i;
//读入数据
cin>>n;
cin>>a>>b>>c;
memset(res,-1,sizeof(res));
memset(pos,-1,sizeof(pos));
//初始化
for (i=n-1; i>=0; i--)//从右向左
{
char a1=a[i]-'A',b1=b[i]-'A',c1=c[i]-'A';//全部转成对应数字下标
if (!usedZiMu[a1]) ///从上往下
{
usedZiMu[a1]=1;
pos[k++] = a1;
}
if (!usedZiMu[b1])
{
usedZiMu[b1]=1;
pos[k++] = b1;
}
if (!usedZiMu[c1])
{
usedZiMu[c1]=1;
pos[k++] = c1;
}
}
//for (i=0; i 测试数据 #0: TimeLimitExceeded, time = 1203 ms, mem = 576 KiB, score = 0
测试数据 #1: Accepted, time = 15 ms, mem = 572 KiB, score = 10
测试数据 #2: Accepted, time = 0 ms, mem = 576 KiB, score = 10
测试数据 #3: Accepted, time = 0 ms, mem = 576 KiB, score = 10
测试数据 #4: Accepted, time = 15 ms, mem = 576 KiB, score = 10
测试数据 #5: Accepted, time = 234 ms, mem = 576 KiB, score = 10
测试数据 #6: TimeLimitExceeded, time = 1015 ms, mem = 576 KiB, score = 0
测试数据 #7: TimeLimitExceeded, time = 1015 ms, mem = 576 KiB, score = 0
测试数据 #8: TimeLimitExceeded, time = 1203 ms, mem = 576 KiB, score = 0
测试数据 #9: TimeLimitExceeded, time = 1203 ms, mem = 576 KiB, score = 0
TimeLimitExceeded, time = 5903 ms, mem = 576 KiB, score = 50
//#include
#include
#include
#include
#include
#include
using namespace std;
int n;//读入几进制0.1.2.3...n-1
int res[26];//保存A.B..Z代表的数字
int used[26];//保存这个对应数字是否被用,因为题目说每个字母只能代表一个数
string a,b,c;//保存加数1,加数2,和
int flag = 0;//是否已找到符合条件的唯一解//加上这个多对了2个点//
//-----最多只能7个点了,原先是从abcd..填字母,改变
char pos[26];//保存从右往左,从上往下的字母出现顺序,判断的时候也按这个顺序判断
int usedZiMu[26];//保存该字母是否已经出现
//剪枝优化函数,来判断当前的字母的数字取法是否可行
//题目就是一个可行与否的问题
int Check()
{
int i;
//看是否满足 a+b==c
for (i=n-1;i>=0;i--)
{
char a1=a[i]-'A',b1=b[i]-'A',c1=c[i]-'A';//取三个数第i位置值
if(res[a1]!=-1 && res[b1]!=-1 && res[c1]!=-1)//3个数都知道-----3个点
{
if( (res[a1]+res[b1])%n!=res[c1] &&//无进位
(res[a1]+res[b1]+1)%n!=res[c1])//有进位
return 0;
}
//加上后面这些多对了1个点
if(res[a1]!=-1 && res[b1]!=-1 && res[c1]==-1)//如果只知道其中2个
{
int sum1,sum2;//sum1无进位,sum2有进位
sum1 = (res[a1]+res[b1])%n;
sum2 = (res[a1]+res[b1]+1)%n;
if (used[sum1] && used[sum2])//可能填在c1的数都用了肯定不行
return 0;
}
if (res[a1]!=-1 && res[b1]==-1 && res[c1]!=-1)//和与一个加数知道
{
int js1,js2;//js1无进位,js2有进位
js1 = (res[c1]-res[a1]+n)%n;
js2 = (res[c1]-res[a1]-1+n)%n;
if (used[js1] && used[js2])//可能填写咋b1位置的数都被用了
return 0;
}
if (res[a1]==-1 && res[b1]!=-1 && res[c1]!=-1)//和与一个加数知道
{
int js1,js2;//js1无进位,js2有进位
js1 = (res[c1]-res[b1]+n)%n;
js2 = (res[c1]-res[b1]-1+n)%n;
if (used[js1] && used[js2])//可能填写咋b1位置的数都被用了
return 0;
}
}
return 1;
}
/*剪枝策略只这样写,数据只过3个点
int Check()
{
int i;
//看是否满足 a+b==c
for (i=0;i<=n-1;i++)
{
char a1=a[i]-'A',b1=b[i]-'A',c1=c[i]-'A';//取三个数第i位置值
if(res[a1]!=-1 && res[b1]!=-1 && res[c1]!=-1)
{
if( (res[a1]+res[b1])%n!=res[c1] &&//无进位
(res[a1]+res[b1]+1)%n!=res[c1])//有进位
return 0;
}
}
return 1;
}
*/
//严格判断当前所有字母的填数满足等式否
int OK()
{
int i;
int jinwei=0;
int jiahe;
for (i=n-1; i>=0; i--)
{
char a1=a[i]-'A',b1=b[i]-'A',c1=c[i]-'A';
jiahe = (res[a1]+res[b1]+jinwei)%n;//计算和
jinwei =( res[a1]+res[b1]+jinwei)/n;//计算进位
if (jiahe!=res[c1]) return 0;
}
if (jinwei>0) return 0;
return 1;
}
void dfs(int k)//深搜,利用系统的堆栈枚举
{
int i;
//if (flag) return ;//已找到解
//if (!Check()) return;//现在的方法不合理--从if (!used[i]&&Check())移到这里多了1个点共7个了
if(k==n)//找到可行解且唯一(题目得知),输出
{
if (OK())//如果当前所有字母填数满足等式则输出
{
for(i=0; i<=n-2; i++) cout<=0; i--)
{
//如果i还没被占用,且满足剪枝条件,则进行下层遍历
if (!used[i]&&Check() )
{
used[i]=1;//i被占用
res[pos[k]]=i;//第k个字母取数字i
dfs(k+1);
used[i]=0;//i被释放,可以被其他字母占用
res[pos[k]]=-1;//第k个字母释放
}
}
return ;
}
int main()
{
int k=0,i;
//读入数据
cin>>n;
cin>>a>>b>>c;
memset(res,-1,sizeof(res));
memset(pos,-1,sizeof(pos));
//初始化
for (i=n-1; i>=0; i--)//从右向左
{
char a1=a[i]-'A',b1=b[i]-'A',c1=c[i]-'A';//全部转成对应数字下标
if (!usedZiMu[a1]) ///从上往下
{
usedZiMu[a1]=1;
pos[k++] = a1;
}
if (!usedZiMu[b1])
{
usedZiMu[b1]=1;
pos[k++] = b1;
}
if (!usedZiMu[c1])
{
usedZiMu[c1]=1;
pos[k++] = c1;
}
}
//for (i=0; i ---------------------------------------
总结:
1、搜索题目因为剪枝的丰富多样性,且因为没有明确的模板剪枝策略,很方便来拉开选手的分数
2、在保证正确性的前提下,尽可能,高校,准确的剪枝,这道题目里面,a+b=c 这个策略是明显的
但是从右向左,从上向下是不容易想到的
3、出题人在出题的时候是先 用数计算,然后挖掉用字母替换,然后写程序来验证的????
-------------------------------------------
多有不当之处,敬请批评指正