洛谷---动态规划---动归---dp
洛谷---动态规划---动归---dp
http://www.luogu.org
动态规划---动归---dp是弱项,需要勤学苦练,先试了《算法竞赛入门经典(第2版)》,发现难度挺大,还是要循序渐进,遂决定,找洛谷,自简单动归题目开始刷起,之前刷过的题,直接跳过。
//P2871 [USACO07DEC]手链Charm Bracelet
//读完题目,发现是01背包问题
//看了数据范围,1 ≤ N ≤ 3,402 1 ≤ M ≤ 12,880二维数组,太大了,改用一维数组
//样例通过,提交AC 2018-1-18
#include
#include
int w[3500],d[3500],f[13000];
int max(int a,int b){
return a>b?a:b;
}
int main(){
int n,m,i,j;
memset(f,0,sizeof(f));
scanf("%d%d",&n,&m);
for(i=1;i<=n;i++)scanf("%d%d",&w[i],&d[i]);
for(i=1;i<=n;i++)
for(j=m;j>=w[i];j--)
f[j]=max(f[j],f[j-w[i]]+d[i]);
printf("%d",f[m]);
return 0;
}
//P2639 [USACO09OCT]Bessie的体重问题Bessie's We…
//读完题目,发现是01背包问题,
//数据范围,1 <= N <= 500) (5 <= H <= 45,000)用二维数组要爆内存,只能采用一维数组
//样例通过,提交AC 2018-1-18 21:20
#include
#include
int a[510],f[45100];
int max(int a,int b){
return a>b?a:b;
}
int main(){
int i,j,h,n;
memset(f,0,sizeof(f));
scanf("%d%d",&h,&n);
for(i=1;i<=n;i++)scanf("%d",&a[i]);
for(i=1;i<=n;i++)
for(j=h;j>=a[i];j--)
f[j]=max(f[j],f[j-a[i]]+a[i]);
printf("%d",f[h]);
return 0;
}
//P2722 总分 Score Inflation
//读完题目,发现是完全背包问题,
//数据范围1 <= N <= 10,000 1 <= M <= 10,000)避免爆内存,只能采用一维数组
//样例通过,提交AC 2018-1-18 21:34
#include
#include
int c[10100],w[10100],f[10100];
int max(int a,int b){
return a>b?a:b;
}
int main(){
int i,j,m,n;
memset(f,0,sizeof(f));
scanf("%d%d",&m,&n);
for(i=1;i<=n;i++)scanf("%d%d",&c[i],&w[i]);
for(i=1;i<=n;i++)
for(j=w[i];j<=m;j++)
f[j]=max(f[j],f[j-w[i]]+c[i]);
printf("%d",f[m]);
return 0;
}
//P2925 [USACO08DEC]干草出售Hay For Sale
//读完题目,发现是01背包问题,
//看数据范围,(1≤C≤50000) (1≤H≤5000),二维数组要爆内存,采用一维数组
//样例通过,提交,竟然 测试点3 TLE 没想到
//翻看题解https://www.luogu.org/problemnew/solution/P2925发现此句"优化,如果已经达到最好的结果(装满),就直接退掉"
//马上修改,提交AC 2018-1-19 收获,装满,无需再装,进行优化
#include
#include
int v[5100],f[50100];
int max(int a,int b){
return a>b?a:b;
}
int main(){
int m,n,i,j;
memset(f,0,sizeof(f));
scanf("%d%d",&m,&n);
for(i=1;i<=n;i++)scanf("%d",&v[i]);
for(i=1;i<=n;i++)
for(j=m;j>=v[i];j--){
f[j]=max(f[j],f[j-v[i]]+v[i]);
if(f[m]==m){//优化,针对测试点3,若已装满,无需再进行计算。
printf("%d",m);
return 0;//直接结束程序
}
}
printf("%d",f[m]);
return 0;
}
//P1964 【mc生存】卖东西
//多重背包,该题比一般的多重背包要难得多,有格子的限制,名字的限制,限制越多,编写越困难
//看了https://www.luogu.org/problemnew/solution/P1964后发现,输入信息有冗余,若名字相同,则bi,ci相同
//还发现格子具有排他性,若放了某种物品,其他物品再也无法放入了。
//多重背包写法,类似 完全背包
//样例通过,测试点2,5 WA
//采用功能替换的方式,将题解中的部分代码,加入程序进行替换,排错,
//认真对完题目,发现,思路,算法都没有错,错在
//每种物品有ai件,价值bi,一格可以放ci个,名字sti 将变量张冠李戴了
//错得太离谱了,将bi与ci的功能弄混了,修改,样例通过,提交AC 2018-1-22 22:01
//此题收获,多重背包更熟练了。该题,在多重背包里,算是比较复杂的。
#include
#include
#define maxn 110
int a[maxn],b[maxn],c[maxn],f[25];//f[i] i格子所放物品最多卖的钱
char s[maxn][maxn];
int cell_num(int a,int c){//返回同一物体所占格子数
if(a%c==0)return a/c;
else return a/c+1;//此处写成 else a/c+1;有失水准
}
int max(int a,int b){
return a>b?a:b;
}
int main(){
int m,n,i,j,k,V,cnt=0,v;
memset(f,0,sizeof(f));//漏了此句
scanf("%d%d",&m,&n);
V=21-m;
for(i=1;i<=n;i++){//读取数据,合并同类项
scanf("%d%d%d%s",&a[i],&b[i],&c[i],s[i]);
for(j=1;j<=cnt;j++)//比较之前是否有雷同物品
if(strcmp(s[j],s[i])==0){//相同 物品
a[j]+=a[i];
break;
}
if(j>cnt)cnt++;
}
for(i=1;i<=cnt;i++)//cnt物品的种类
for(j=V;j>=0;j--)
for(k=0;k<=a[i];k++){//物体可放0个,也可放a[i]个
v=cell_num(k,c[i]);//此处写成v=cell_num(k,b[i]);这是真的有失水准了//此处写成 v=cell_num(k,c[i]);有失水准
if(j
}
printf("%d",f[V]);
return 0;
}
//P1910 L国的战斗之间谍
//01背包问题,有三个条件限制,个数,能力,钱
//将三维数组 降维 二维数组
//样例通过,提交,看了测试数据吓了一跳,足足有20个测试点
//还好AC了,2018-1-23
//对超时解释,1≤n≤100,1≤m≤1000, 1≤x≤1000 时间复杂度 100*1000*1000=1e8,可以预测 实际测试数据 没有这么大范围。
#include
#include
#define maxn 1100
int a[maxn],b[maxn],c[maxn],f[maxn][maxn];
int max(int a,int b){
return a>b?a:b;
}
int main(){
int n,m,x,i,j,k;
memset(f,0,sizeof(f));
scanf("%d%d%d",&n,&m,&x);
for(i=1;i<=n;i++)scanf("%d%d%d",&a[i],&b[i],&c[i]);//A(能得到多少资料)、B(伪装能力有多差)、C(要多少工资)
for(i=1;i<=n;i++)
for(j=m;j>=b[i];j--)
for(k=x;k>=c[i];k--)
f[j][k]=max(f[j][k],f[j-b[i]][k-c[i]]+a[i]);
printf("%d",f[m][x]);
return 0;
}
//P1507 NASA的食物计划
//读完题目,发现是01背包,有三个约束条件,体积,质量,卡路里
//f[i][j][k] 选前i种物体,j体积,k质量,f[i][j][k]卡路里的值
//样例通过,提交AC 2018-1-19 很高兴,水平提升,实实在在看得见。
#include
#include
int a[55],b[55],c[55],f[55][410][410];
int max(int a,int b){
return a>b?a:b;
}
int main(){
int i,j,k,n,V,M;
memset(f,0,sizeof(f));
scanf("%d%d%d",&V,&M,&n);
for(i=1;i<=n;i++)scanf("%d%d%d",&a[i],&b[i],&c[i]);
for(i=1;i<=n;i++)
for(j=1;j<=V;j++)
for(k=1;k<=M;k++)
if(j>=a[i]&&k>=b[i]){//同时满足体积,质量都能装进
f[i][j][k]=max(f[i-1][j][k],f[i-1][j-a[i]][k-b[i]]+c[i]);
}else f[i][j][k]=f[i-1][j][k];
printf("%d",f[n][V][M]);
return 0;
}
//P2430 严酷的训练
//读完题目,发现是01背包问题,从数据角度考虑,题目总数<=5000,规定时间<=5000 考虑用一维数组
//该题,就是数据读取这块需要花点时间
//样例通过,提交,测试点2-5 WA
//读了一遍代码,发现f[]初始化忘记了。以及 for(j=T;j>=b[c[i]];j--)//此处写成 for(j=T;j>=b[i];j--)
//修改,提交AC 2018-1-19
#include
#include
int a[5100],b[5100],c[5100],d[5100],f[5100];//a[i] 知识点i老王耗时 b[i]知识点i WKZ耗时
int max(int a,int b){
return a>b?a:b;
}
int main(){
int e1,e2,m,n,i,j,k,T;
memset(f,0,sizeof(f));//漏了该句初始化
scanf("%d%d",&e1,&e2);//e1 WKY水平,e2 老王水平
scanf("%d%d",&m,&n);
for(i=1;i<=n;i++)scanf("%d",&a[i]),b[i]=a[i]*e2/e1;
for(i=1;i<=m;i++)scanf("%d%d",&c[i],&d[i]);//c[i]所属知识点 d[i]奖励值
scanf("%d",&T);
for(i=1;i<=m;i++)
for(j=T;j>=b[c[i]];j--)//此处写成 for(j=T;j>=b[i];j--)
f[j]=max(f[j],f[j-b[c[i]]]+d[i]);
printf("%d",f[T]);
return 0;
}
//P1802 5倍经验日
//读完题目,发现是部分背包问题
//采用二维数组
//翻看解答,发现想多了,还是01背包问题,分两种,一种,什么药都不用,一种用药能打赢
//样例通过,提交,测试点10 WA
//再次翻看题解,发现要讲int 改成 long long
//修改,提交AC 2018-1-19
#include
#include
int lose[1100],win[1100],use[1100];
long long f[1100][1100];
long long max(long long a,long long b){
return a>b?a:b;
}
int main(){
int n,x,i,j;
memset(f,0,sizeof(f));
scanf("%d%d",&n,&x);
for(i=1;i<=n;i++)scanf("%d%d%d",&lose[i],&win[i],&use[i]);
for(i=1;i<=n;i++)
for(j=0;j<=x;j++)
if(j
else f[i][j]=max(f[i-1][j]+lose[i],f[i-1][j-use[i]]+win[i]);
printf("%lld",5*f[n][x]);
return 0;
}
//P1802 5倍经验日
//读完题目,发现是部分背包问题
//采用二维数组
//翻看解答,发现想多了,还是01背包问题,分两种,一种,什么药都不用,一种用药能打赢
//样例通过,提交,测试点10 WA
//再次翻看题解,发现要讲int 改成 long long
//修改,提交AC 2018-1-19
//继续修改,将二维数组改成一维数组 ,样例通过,提交,测试点2,测试点4-10WA
//修改,提交AC,该题收获,将二维改成一维,还是有需要注意的地方,一维完全根据二维来写,
//for(i=1;i<=n;i++)
// for(j=0;j<=x;j++)
// if(j
// else f[i][j]=max(f[i-1][j]+lose[i],f[i-1][j-use[i]]+win[i]);
//根据上述代码,写出了一维数组,才不会错。
#include
#include
int lose[1100],win[1100],use[1100];
long long f[1100];
long long max(long long a,long long b){
return a>b?a:b;
}
int main(){
int n,x,i,j;
memset(f,0,sizeof(f));
scanf("%d%d",&n,&x);
for(i=1;i<=n;i++)scanf("%d%d%d",&lose[i],&win[i],&use[i]);
for(i=1;i<=n;i++)
for(j=x;j>=0;j--)//此处写成 for(j=x;j>=use[i];j--)测试点2,测试点4-10WA
if(j>=use[i])f[j]=max(f[j]+lose[i],f[j-use[i]]+win[i]);//此处写成 f[j]=max(f[j]+lose[i],f[j-use[i]]+win[i]);测试点2,测试点4-10WA
else f[j]=f[j]+lose[i];
printf("%lld",5*f[x]);
return 0;
}
//P1968 美元汇率
//基本确定,问题属线性动态规划
//但感觉无从下手。
//https://www.luogu.org/problemnew/solution/P1968此文代码写得不错
//仿照编写,样例通过,提交AC 2018-1-19
#include
double max(double a,double b){
return a>b?a:b;
}
int main(){
int n,i,j,a;
double dp1=100,dp2=0,t;//dp1换成 当前 最多的美元值 dp2换成 当前 最多的马克值
scanf("%d",&n);
for(i=1;i<=n;i++){
scanf("%d",&a);
t=dp1,dp1=max(dp1,dp2*100/a),dp2=max(dp2,t*a/100);//美元由马克来, 马克由美元来 100美元兑 a马克 ;a马克 兑 100美元
}
printf("%.2lf",dp1);
return 0;
}
// P1734 最大约数和
//没啥思路,看了解答,发现可以简化成01背包问题,真是没想到,开眼了。
//https://www.luogu.org/problemnew/solution/P1734此文思路介绍得真不赖啊
//样例通过,提交AC 2018-1-19 该题有收获,转成01背包问题,建模很关键
#include
#include
int w[1100],c[1100],f[1100];
int max(int a,int b){
return a>b?a:b;
}
int factor(int a){//a对应的约数和
int i,ans=0;
for(i=1;i
ans+=i;
return ans;
}
int main(){
int n,i,j;
scanf("%d",&n);
for(i=1;i<=n;i++)w[i]=i,c[i]=factor(i);
for(i=1;i<=n;i++)
for(j=n;j>=w[i];j--)
f[j]=max(f[j],f[j-w[i]]+c[i]);
printf("%d",f[n]);
return 0;
}
//P1359 租用游艇
//f[i][j] i->j的最少租金
//此题有感觉,但又觉得编起来比较混乱。
//样例通过,提交,测试点2-12 WA
//https://www.luogu.org/problemnew/solution/P1359?&page=3此文代码写得真不赖
//样例通过,提交AC 2018-1-19 17:11
#include
#include
int f[210][210];
int min(int a,int b){
return a
int main(){
int n,i,j,k;
scanf("%d",&n);
memset(f,127,sizeof(f));//漏了此句
for(i=1;i
scanf("%d",&f[i][j]);
for(i=1;i
for(k=i+1;k<=j-1;k++)
f[i][j]=min(f[i][j],f[i][k]+f[k][j]);
printf("%d",f[1][n]);
return 0;
}
//P1926 小书童——刷题大军
//基本思路,做两次01背包,
//样例通过,提交AC 2018-1-20 20:07真没想到一次性能通过
//f[i][j] 用来记录选 前i题,消耗的时间 j 能取得的最多成绩
//f[m][j]>=k用来找取得及格,需要消耗的最小空间j,让q=j
//g[i][j]用来记录 选 前i题,消耗的时间j 能做的最多题数 请注意,这种情况下 最大的空间 r-q;
#include
#include
int a[15],b[15],c[15],f[15][160],g[15][160];
int max(int a,int b){
return a>b?a:b;
}
int main(){
int n,m,k,r,i,j,q;
memset(f,0,sizeof(f)),memset(g,0,sizeof(g));
scanf("%d%d%d%d",&n,&m,&k,&r);
for(i=1;i<=n;i++)scanf("%d",&a[i]);
for(i=1;i<=m;i++)scanf("%d",&b[i]);
for(i=1;i<=m;i++)scanf("%d",&c[i]);
for(i=1;i<=m;i++)
for(j=1;j<=r;j++)
if(j
for(j=1;j<=r;j++)
if(f[m][j]>=k){
q=j;
break;
}
for(i=1;i<=n;i++)
for(j=1;j<=r-q;j++)
if(j
printf("%d",f[n][r-q]);
return 0;
}
//P1044 栈
//该题也就 序列的总数目 能与动态规划 挂上联系
//但感觉无从下手,栈与动态规划跨度太大。
//翻看解答,代码是如此之短,不过,确实是想不到。
//P1044 栈
//此文思路介绍不错https://www.luogu.org/problemnew/solution/P1044摘抄如下
//看到大家的题解都写到了卡特兰数,但是没有细细的讲讲这跟本题有什么关系
//本题的描述十分简单。n个数依次进栈,可随机出栈。求有几种可能。
//dfs可以解,但是递推仿佛好像如同看上去貌似更简单一些。
//解释一下原理:
//建立数组f。f[i]表示i个数的全部可能性。
//f[0] = 1, f[1] = 1; //当然只有一个
//设 x 为当前出栈序列的最后一个,则x有n种取值
//由于x是最后一个出栈的,所以可以将已经出栈的数分成两部分
//比x小
//比x大
//比x小的数有x-1个,所以这些数的全部出栈可能为f[x-1]
//比x大的数有n-x个,所以这些数的全部出栈可能为f[n-x]
//这两部分互相影响,所以一个x的取值能够得到的所有可能性为f[x-1] * f[n-x]
//另外,由于x有n个取值,所以
//ans = f[0]*f[n-1] + f[1]*f[n-2] + ... + f[n-1]*f[0];
//这,就是传说中的卡特兰数
//样例通过,试了一下n=18,发现int没有溢出,提交AC 2018-1-24 21:10
#include
int f[20];
int main(){
int i,j,n;
scanf("%d",&n);
f[0]=1,f[1]=1;
for(i=2;i<=n;i++)
for(j=0;j<=i-1;j++)
f[i]+=f[j]*f[i-j-1];
printf("%d",f[n]);
}
//P1679 神奇的四次方数
//此题与 P1734 最大约数和 比较接近,但又有不同
//编到不能编,翻看题解,发现跟想的不一样,首先误认为是01背包,结果是完全背包,还有一个不会统计个数
//样例通过,提交AC 2018-1-21 15:33
#include
#include
int c[20],n,f[100100];
int fourth_power(int n){
int i;
for(i=1;i*i*i*i<=n;i++)
c[i]=i*i*i*i;
return i;
}
int min(int a,int b){
return a
int main(){
int m,i,j;
memset(f,127,sizeof(f)),f[0]=0;//别忘了初始化f[0]=0;
scanf("%d",&n);
m=fourth_power(n);
for(i=1;i<=m;i++)
for(j=c[i];j<=n;j++)
f[j]=min(f[j],f[j-c[i]]+1);
printf("%d",f[n]);
return 0;
}
//P2362 围栏木桩
//读完题目,发现是最长上升子序列问题
//做着做着,突然发现,方案数是难点.
//翻看https://www.luogu.org/problemnew/solution/P2362发现方案数想是想到了一点做法,但实施起来还有有相当差距
//样例通过,提交,测试点1 WA
//翻看该题讨论https://www.luogu.org/discuss/show?postid=23029
//得到了一组输入输出数据
//输入
//2 10 1 3 4 5 6 7 8 9 2 10
//20 1 2 3 4 5 6 7 8 9 10 1 2 3 4 5 6 7 8 9 10
//输出
//https://www.luogu.org/recordnew/show/5028646此文代码写得不错
//修改,提交AC 2018-1-21 19:59 此文收获,学习了写方案数
#include
int d[160],a[160],f[160];//f[i]记录方案数
int main(){
int m,i,j,n,c,max;
scanf("%d",&m);
while(m--){
max=-1,c=0;
scanf("%d",&n);
for(i=1;i<=n;i++){
scanf("%d",&a[i]);
d[i]=1,f[i]=1;//此处写成 f[i]=0
for(j=1;j
if(d[j]+1>d[i])d[i]=d[j]+1,f[i]=f[j];//f[i]=f[j]该句没写好 ,此句写成f[i]++;
else if(d[j]+1==d[i])f[i]+=f[j];//此句写成f[i]++//此句考虑到了
if(max
for(i=1;i<=n;i++)
if(max==d[i])c+=f[i];
printf("%d %d\n",max,c);
}
return 0;
}
//P2800 又上锁妖塔
//反复读题,看输入输出样例,竟然弄不懂题意。
//搜了一遍 仙剑 锁妖塔,还是弄不明白题意
//https://www.luogu.org/problemnew/solution/P2800?&page=2翻看题解,思路摘抄如下:
//DP 到达第i层分为三种情况:
// 从i-2层跳上来的f[i-3]+h[i-2]//即飞了i-1这层高度,i这层高度,共计2层 i-2这层必须爬,才能有接下来的飞 2层
// 从i-1层跳上来的f[i-2]+h[i-1]//即飞了i这层高度,共计1层,i-1这层必须爬,才能有接下来的飞 1层
// 从i-1层爬上来的f[i-1]+h[i]//即直接爬了i这层高度
//三种情况取最小值 该题三种情况 说说比较难理解,还是配一幅图比较容易理解。f[i]到达i层最短时间 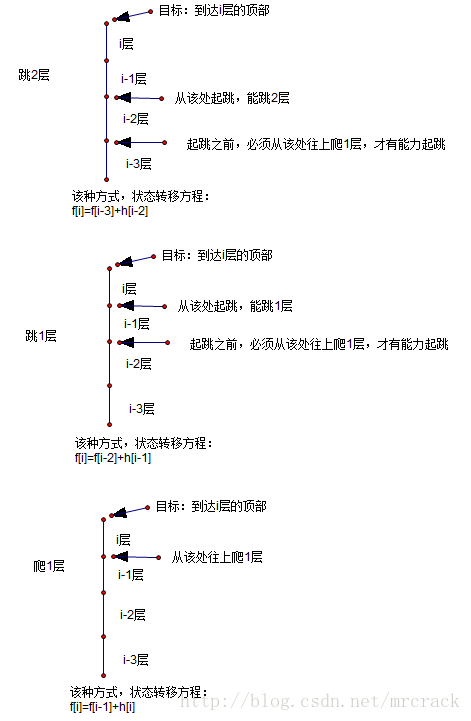
//该题语意不清,这样解释,跳两次一层再爬一层,爬的这层高度大小,即该层所消耗的时间
//样例通过,提交AC 2018-1-23
#include
#define maxn 1000100
int h[maxn],f[maxn];//h[i]第i层高度 f[i]到达第i层顶部 消耗的 最短时间
int min(int a,int b){
return a
int main(){
int n,i;
scanf("%d",&n);
for(i=1;i<=n;i++)scanf("%d",&h[i]);
f[2]=f[1]=0;
for(i=3;i<=n;i++)f[i]=min(f[i-1]+h[i],min(f[i-2]+h[i-1],f[i-3]+h[i-2]));
printf("%d",f[n]);
return 0;
}
//P1832 A+B Problem(再升级)
//统计<=n的素数,
//采用完全背包
//担心int 不够用,输入1000测试了一遍,还好,没有溢出。
//样例通过,提交,测试点2,10RE 测试点3,5-9WA
//修改,提交,测试点2,3,5-10 WA
//再次对1000进行测试,发现int要溢出,改成long long
//样例通过,提交AC 2018-1-22
#include
#include
int c[1100];
long long f[1100];
int isPrime(int n){//判断素数
int i;
if(n==1)return 0;//非素数
if(n==2)return 1;//素数
for(i=2;i*i<=n;i++)
if(n%i==0)return 0;//非素数
return 1;//素数
}
int main(){
int cnt=0,i,j,n;
memset(f,0,sizeof(f)),f[0]=1;//f[0]=1什么都不选,也是一种情况。
scanf("%d",&n);
for(i=1;i<=n;i++)
if(isPrime(i))cnt++,c[cnt]=i;
for(i=1;i<=cnt;i++)
for(j=c[i];j<=n;j++)//此处写成 for(j=c[1];j<=n;j++) 出昏招了,造成 测试点2,10RE 测试点3,5-9WA
f[j]+=f[j-c[i]];//此句写成 f[j]=max(f[j],f[j-c[i]]+1); 积累不够啊 测试点2,3,5-10 WA
printf("%lld",f[n]);
return 0;
}
//P1130 红牌
//读完题目,感觉用图的最短路径进行处理,但又感觉限制太多,无从下手。
//翻看https://www.luogu.org/problemnew/solution/P1130题解,发现类似数字三角形,真是没想到啊
//样例的实现过程如图所示,确实是数字三角形这种类型的问题
//上述过程图编程实现不易,并且思路混乱,重作一副过程图

//在对输入数据的行列要更换时,建议输入结束后,要将结果输出打印一遍,看看是否符合自己的要求,没问题了,才能往下编,否则查错要查好长时间。
//事实证明,上述说法,在调试过程中,十分有用。
//动态转移方程f[i][j]=min(f[i-1][j-1],f[i-1][j])+a[i][j];//f[i][j] i步 j方法数中 最短时间
//样例通过,提交AC 2018-1-24
//将二维数组 改成 一维数组 提交 测试点2-4,7-9 WA
//不再修改,到此结束。还是采用二维数组
#include
int a[2100][2100],f[2100][2100];//a[i][j] i步数 j方法数
int min(int a,int b){
return a
int main(){
int n,m,i,j,ans=999999999;
scanf("%d%d",&n,&m);//请注意,N和M,表示步数和小组数 下面使用N,M若不注意,容易出错
for(j=1;j<=m;j++)
for(i=1;i<=n;i++)
scanf("%d",&a[i][j]);
for(j=0;j<=m;j++)f[0][j]=0;//此行,之前写在下面语句之后//此处写成 for(j=1;j<=m;j++)f[0][j]=0;
for(i=1;i<=n;i++)
for(j=1;j<=m;j++)
f[i][j]=min(f[i-1][j-1],f[i-1][j])+a[i][j],f[i][0]=f[i][m];//f[i][0]=f[i][m]此句很关键
for(j=1;j<=m;j++)
if(f[n][j]
return 0;
}
//P2719 搞笑世界杯
//没啥感觉,以为难在数学
//http://codevs.cn/wiki/solution/?problem_id=1060此文思路还行,摘抄如下:
//d[a][b]表示剩a张A类票和b张B类票时,最后两张票相同的概率
//那么此时的排队的第一个人只有两种选择
//拿A类票或者B类票
//抛硬币得到的可能性当然是二分之一,所以说d[i-1][j](当前第一人拿了A类票)和d[i][j-1](当前第一人拿了B类票)各占二分之一
//http://blog.csdn.net/LOI_DQS/article/details/49127021此文思路写得比较简洁,摘抄如下:
//定义:dp[i][j]为还剩i张a类票,j张b类票,最后两张相同的概率。
//易得出dp[i][0]=dp[0][i]=1.0 (i>=2)
//多出一张票,不管是A类还剩B类,概率都是0.5。
//所以状态转移方程:
//dp[i][j]=dp[i-1][j]*0.5+dp[i][j-1]*0.5
//请注意,该算法是逆推,从确定的结果开始
//动态规划,此题有一定心的,要从结果确定的位置开始推
//样例通过,提交AC 2018-2-1
//f[i][j] 剩i张A票 ,j张B票,最后两张票相同的概率,这点很难想到,什么时候能想到了,水平自然上台阶了。
#include
double f[1260][1260];
int main(){
int n,i,j;
scanf("%d",&n);
n/=2;
for(i=2;i<=n;i++)f[i][0]=f[0][i]=1;
for(i=1;i<=n;i++)
for(j=1;j<=n;j++)
f[i][j]=f[i-1][j]*0.5+f[i][j-1]*0.5;
printf("%.4lf",f[n][n]);
return 0;
}
//P1757 通天之分组背包
//感觉不难,但又无从下手
//隔了几个小时,决定,还是看看题解
//瞟了一眼,分组背包,发现曾今编写过,http://blog.csdn.net/mrcrack/article/details/78440134详见 1272 【例9.16】分组背包
//摘抄如下:
//1272 【例9.16】分组背包
//https://www.cnblogs.com/z360/p/6366074.html此文思路不错,摘抄如下:
//这个问题变成了每组物品有若干种策略:是选择本组的某一件,还是一件都不选。
//也就是说设f[k][v]表示前k组物品花费费用v能取得的最大权值,
//则有f[k][v]=max{f[k-1][v],f[k-1][v-w[i]]+c[i]|物品i属于第k组}。
//使用一维数组的伪代码如下:
//for 所有的组k for v=V..0
//for 所有的i属于组k
//f[v]=max{f[v],f[v-w[i]]+c[i]}
//注意这里的三层循环的顺序,
//“for v=V..0”这一层循环必须在“for 所有的i属于组k”之外
//。这样才能保证每一组内的物品最多只有一个会被添加到背包中。
//另外,显然可以对每组中的物品应用完全背包中“一个简单有效的优化”。
//http://www.cnblogs.com/zzyh/p/6749387.html此文代码写得不错
//样例通过,提交,测试点5 WA
//删除//if(j
//翻看http://ybt.ssoier.cn:8088/problem_show.php?pid=1272 测试数据,才弄白原因,原来给的数据未必是按规则出牌,提
供一组测试数据以供参考
输入:
178 5 4
40 555 1
66 333 3
38 1594 3
173 1840 1
99 1186 1
if(j>=w)正确输出:
2780
if(j
2149
经过一番跟踪,弄明白了,if(j
q=a[i][k];//物品序号
W[q]未必是随q单调递减,break;之后,可能还存在数据j>=w[q],但因为break;的原因,之后数据再没有尝试的机会了。上述原因,整整跟踪了两个小时,总算明白了,if(j
#include
#include
int a[1100],b[1100],c[110][1100],f[1100];//c[][]用来记录 分组的 物品 与 物品呈现序列的对应关系
int max(int a,int b){
return a>b?a:b;
}
int main(){
int m,n,i,j,k,p,cnt=0,w;//m总重量 n件物品
memset(c,0,sizeof(c)),memset(f,0,sizeof(f));
scanf("%d%d",&m,&n);
for(i=1;i<=n;i++){
scanf("%d%d%d",&a[i],&b[i],&p);
c[p][++c[p][0]]=i;//c[p][0]存储p组的物品个数
cnt=max(cnt,p);//cnt统计组数
}
for(i=1;i<=cnt;i++)//请注意,第一个循环是 组数
for(j=m;j>=0;j--)
for(k=1;k<=c[i][0];k++){
p=c[i][k],w=a[p];
if(j>=w)f[j]=max(f[j],f[j-w]+b[p]);//ai,bi,表示物品的重量,利用价值
}
printf("%d",f[m]);
return 0;
}
//P2782 友好城市
//第一步,对南岸自小到大排序 快排
//第二步,对北岸求最长上升子序列
//样例通过,提交,吓了一跳,有20个测试点
//测试点11-15 RE 测试点16-20 TLE
//重新看了数据范围,1<=N<=2e5, 两层循环,确实有问题,在动态规划处理这里需要大改
//看了题解,发现优化还得放一放,过一段时间再来处理该题,2018-1-21 20:52
#include
struct node{
int a,b;
}q[200100],q_t;
int d[200100];
void quicksort(int left,int right){
int i=left,j=right,mid=q[(left+right)/2].a;
while(i<=j){
while(q[i].a
if(i<=j)q_t=q[i],q[i]=q[j],q[j]=q_t,i++,j--;
}
if(left
int main(){
int n,i,j,max=-1;
scanf("%d",&n);
for(i=1;i<=n;i++)scanf("%d%d",&q[i].a,&q[i].b);
quicksort(1,n);
for(i=1;i<=n;i++){
d[i]=1;
for(j=1;j
if(max
printf("%d",max);
return 0;
}
//P2663 越越的组队
//01背包
//100*100/2=5000最大容量
//N=100 5000故采用一维数组
//样例通过,提交AC 2018-1-23 18:06
#include
#include
int c[110],f[5100];
int max(int a,int b){
return a>b?a:b;
}
int main(){
int n,m=0,i,j;
memset(f,0,sizeof(f));
scanf("%d",&n);
for(i=1;i<=n;i++)scanf("%d",&c[i]),m+=c[i];
m/=2;
for(i=1;i<=n;i++)
for(j=m;j>=c[i];j--)
f[j]=max(f[j],f[j-c[i]]+c[i]);
printf("%d",f[m]);
return 0;
}
//P1796 汤姆斯的天堂梦_NOI导刊2010提高(05)
//该题,输入输出格式,解释看不懂啊
//翻了他人解题说明,解释该题输入数据的,一个没有,
//费了老大劲,对照样例与图例,弄明白了,解释如下 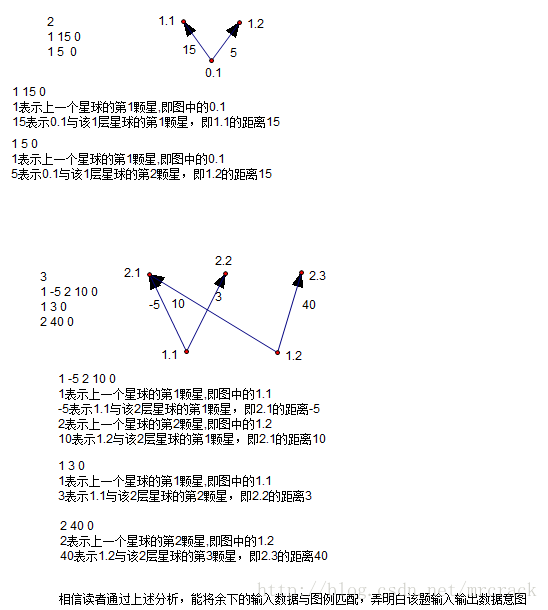
//思路很多,想用Floyd算法,但标记点遇到了困难
//采用数字三角形的动态规划,记录点与点之间的距离遇到了困难
//改进方法,此问题自然解决。
//https://www.luogu.org/problemnew/solution/P1796翻了题解,觉得动态规划写得不错
//思路摘抄如下:
//一道比较简单的动态规划题,类似于数塔,有从上到下和从下到上两种解法,
//以i为等级,j为编号,L表示第i级编号j的星球到第i-1级编号k动态规划方程:f[i,j]=min{f[i-1,j]+L}
//样例通过,提交AC 2018-1-30 17:35
#include
#include
int f[110][110];
int min(int a,int b){
return a
int main(){
int n,k,i,j,b,c,ans;
memset(f,127,sizeof(f));
for(j=0;j<=110;j++)f[0][j]=0;//该句初始化别忘了
scanf("%d",&n);
for(i=1;i<=n;i++){
scanf("%d",&k);
for(j=1;j<=k;j++){
scanf("%d",&b);
while(b){
scanf("%d",&c);
f[i][j]=min(f[i][j],f[i-1][b]+c);
scanf("%d",&b);
}
}
}
for(j=1;j<=k;j++)
ans=min(ans,f[n][j]);
printf("%d",ans);
return 0;
}
//P1796 汤姆斯的天堂梦_NOI导刊2010提高(05)
//该题,输入输出格式,解释看不懂啊
//翻了他人解题说明,解释该题输入数据的,一个没有,
//费了老大劲,对照样例与图例,弄明白了,解释如下
//思路很多,想用Floyd算法,但标记点遇到了困难
//采用数字三角形的动态规划,记录点与点之间的距离遇到了困难
//改进方法,此问题自然解决。
//https://www.luogu.org/problemnew/solution/P1796翻了题解,觉得动态规划写得不错
//思路摘抄如下:
//一道比较简单的动态规划题,类似于数塔,有从上到下和从下到上两种解法,
//以i为等级,j为编号,L表示第i级编号j的星球到第i-1级编号k动态规划方程:f[i,j]=min{f[i-1,j]+L}
//样例通过,提交AC 2018-1-30 17:35
//将二维数组,改成两个一维数组
//样例通过,提交AC 2018-1-30 18:05
#include
#include
#define INF 999999999;
int f[110],t[110];//f[]当前层,t[]之前层
int min(int a,int b){
return a
int main(){
int n,k,i,j,b,c,ans;
for(j=0;j<=110;j++)t[j]=0;//该句初始化别忘了
scanf("%d",&n);
for(i=1;i<=n;i++){
scanf("%d",&k);
for(j=1;j<=k;j++){
scanf("%d",&b),f[j]=INF;//初始化别忘了 f[j]=INF
while(b){
scanf("%d",&c);
f[j]=min(f[j],t[b]+c);
scanf("%d",&b);
}
}
for(j=1;j<=k;j++)t[j]=f[j];
}
for(j=1;j<=k;j++)
ans=min(ans,f[j]);
printf("%d",ans);
return 0;
}
