快速平方根倒数算法

在3D游戏中，要计算物体外观的颜色，比如一束光打在物体上，如何计算顶点和光线之间的角度，我们使用的一般是法线，不可能为每个平面都指定一个法线，我们需要做的就是生成法线，并且对于光照计算，所有的法线向量必须进行规范化，然后再参与计算，这里的向量规范化，就要用到平方根倒数算法，并且这个算法用的非常的频繁。我也是无意中看到就记录下来。本身计算公式是\(y=\frac{1}{\sqrt{x}}\)。

代码

float fast_inverse_sqrt(float x)
{
    float half_x = 0.5 * x;
    int i = *((int *)&x); // 以整数方式读取X
    i = 0x5f3759df - (i>>1); // 神奇的步骤
    x = *((float *)&i); // 再以浮点方式读取i
    x = x*(1.5 - (half_x * x * x)); // 牛顿迭代一遍提高精度
    return x;
} 

整个代码是用C++语法写的，代码中的第一步就是为了计算出变量，之后使用这个变量来进行牛顿迭代法，这里使用牛顿迭代就是为了提高精度。

下面就是以整型int的方式来读取这个浮点数，这样做的原因就是浮点型的平方根倒数的结果和整型是相关的。下面就看看推导关系。

推导

在计算机组成原因中得知，IEEE 754标准的32位单精度浮点的表示格式

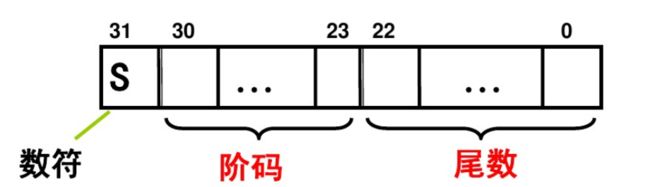
其中阶码\(e\)有八位，尾数\(m\)有23位，数符\(s\)是1位，这样表示出的浮点数的具体数值就是\((-1)^s(1+m)2^{e-127}\)，因为在平方根中，数一定是正的，所以数符不管，那么最终读取出来的就是\((1+m)\cdot2^{e_x}\)。之后使用整型来读取的话，依旧读取的是阶码\(e\)和尾数\(m\)，那么它表示的数就是\(E\cdot2^{23}+M\)，这里的\(E\)和上面的\(e_x\)是有区别的，上面的\(e_x\)减去了127的，因而可以转化得知\(e_x=E-127\)，上面的\(m\)和\(M\)也是不同的，\(m\)本身是小数，范围是\([0,1)\)，但是\(M\)是整数，范围是\([0，2^23-1]\)，因此可以根据这个转化为\(m=\frac{M}{L}\)，其中\(L=2^{23}\)。根据上面的描述，可以得到俩个转化的公式为：

\[e_x=E-B,B=127 \\ m=\frac{M}{L},L=2^{23} \]

下面对倒数平方根公式进行推导

\[y = \frac{1}{\sqrt{x}} \]

俩边取对数得到

\[log_2y = -\frac{1}{2}log_2x \]

俩边的\(x\)和\(y\)都是浮点数，都可以用浮点数来表示

\[log_2((1+m_y)2^{e_y}) = -\frac{1}{2}log_x((1+m_x)2^{e_x})\\ log_2(1+m_y) + e_y = -\frac{1}{2}[log_x(1+m_x)+e_x] \]

公式的俩边都有\(log_2(1+m)\)，因为\(m\)的取值范围是\([0,1)\)，根据高等数学中的泰勒展开

\[In(1+x)=\sum\limits_{n=1}^\infty\frac{(-1)^{n+1}}{n}x^n \]

可以将\(log_2(1+m)\)转化为\(x+\sigma\)，

\[m_y+\sigma+e_y = -\frac{1}{2}[m_x+\sigma +e_x] \]

将上述得到的转化公式

\[e_x=E-B,B=127 \\ m=\frac{M}{L},L=2^{23} \]

代入其中得到

\[\frac{M_y}{L} + \sigma + E_y - B = -\frac{1}{2}[\frac{M_x}{L} + \sigma + E_x - B] \]

对之进行移项合并之后得到

\[\frac{3}{2}L(\sigma - B) + M_y + LE_y = -\frac{1}{2}(M_x + LE_x) \]

式子中的\(M+LE\)就是整型读取，将之表示为\(I\)，公式变成如下

\[I_y = -\frac{1}{2}I_x + \theta , \theta = \frac{3}{2}L(\sigma - B) \]

这里的\(\theta\)就是上面的0x5f3759df，

    i = 0x5f3759df - (i>>1); // 神奇的步骤

因此第三步的移位操作就是乘以\(\frac{1}{2}\)，之后与\(\theta\)相减，整个过程可以用上述的公式所表示，之后再用浮点读取出来，最终使用牛顿法再一次提高精度。

总结

这个算法对比普通的算法来说，特别快，个人感觉因为使用了底层存储原理，因而这个算法不通用，存储方式发生改变的话，这个算法就不能成功，不过这个算法很厉害。将底层原理和数学结合来产生出这样一种写法。

这个代码最神奇的就是第三步，采用移位的操作。其实算法利用的是底层的浮点数的存储方式。首先将浮点数用整型的方式来读取数据，这里的整型的值等于EL+M。再将浮点数以存储形式来带入平方根倒数式子中进行计算。以x+b来近似log(1+x)，化简式子，之后将式子中的数值转为整型方式读取二进制的形式。之后合并，利用I=EL+M进一步化简得到一个线性的式子，并且试出b的大小，y= -1/2*x+b，那么直接利用这个式子移位操作，再转换成浮点型，就能得出结果，并且为了精确，还可以再进行一次牛顿迭代法来精确。