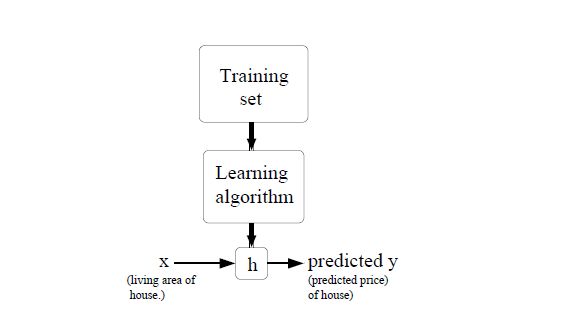
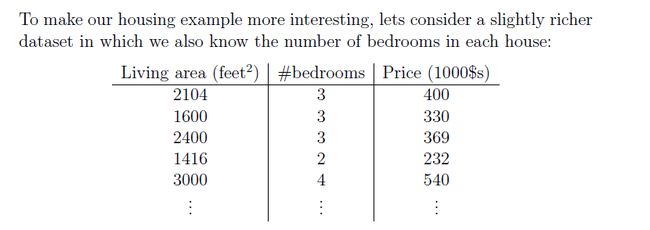
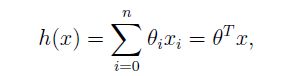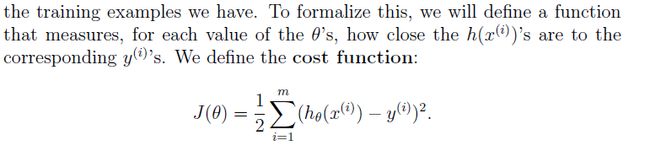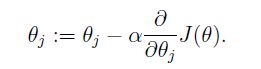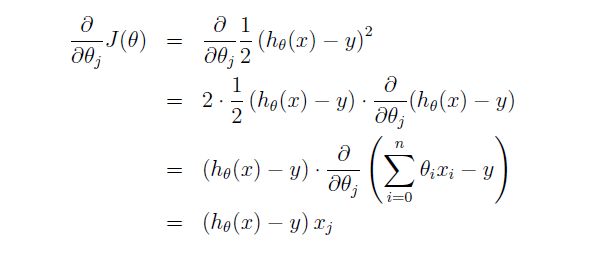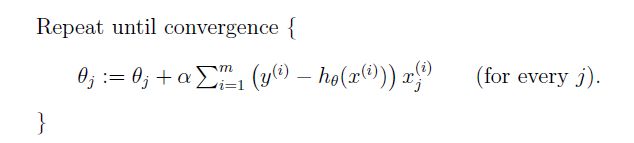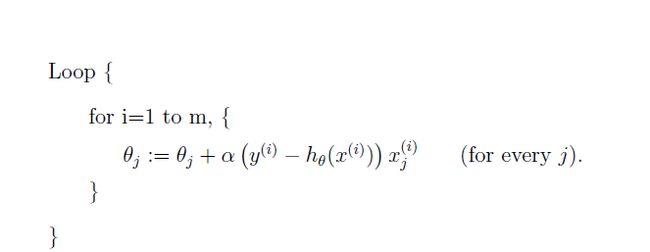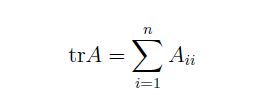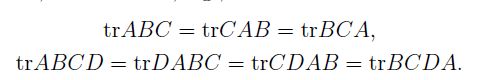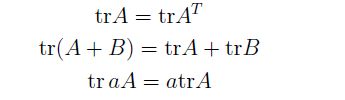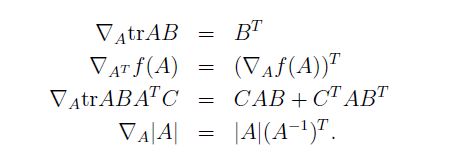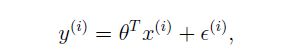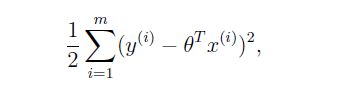监督学习&回归问题(Regression)

---

分类

模型如下：

1. 回归问题：学习的结果是连续的，比如房价等等
2. 分类问题：学习的结果是非连续的，分成某几个类

梯度下降

例子：
：

条件：

• 对于输入X有n个特征值。X = { x1,x2,x3,x4,.......,xn x 1 , x 2 , x 3 , x 4 , . . . . . . . , x n }
• 一共有m组输入。 X1,X2,......,Xm X 1 , X 2 , . . . . . . , X m

结果：

• 根据给出的数据得到函数 hθ h θ (x)，关于 θ θ 的一个函数
• 
  

假设：

• 
• J(θ) J ( θ ) 主要用来描述该方程在样本点的逼近程度

特点：

• 都具有局部最小值
• 最后的结果并不一定是总体的最小值

1.批梯度下降：

• 思路：
  先初始化 θ θ = 0向量，然后通过学习，不断改变 θ θ 使 Jθ J θ 不断减小，致使方程不断在学习点逼近真值。（至于为什么要选择最小二乘法和为什么这个值有极限，稍后给出证明）

• 迭代方程：
  
  其中：

  • α α 决定下降速度

• 推导方程：
  

  迭代算法：
  

• 注意：

  • 该算法每次迭代查看了所有样本，知道 θ θ 收敛
  • 收敛的意思是：误差在允许的范围内就没有继续发生变化了

2.增量梯度下降：

• 迭代算法：
  

• 注意：

  • 每次迭代只用到了第 i i 个样本

正规方程组

1.矩阵导数

• 表示：
  对矩阵A的导数，函数 f f 是一个由矩阵到实数的映射
  

• 矩阵的迹：
  

• 相关的性质：

  • 交换性，要就矩阵的乘法有意义：
    

  • 

  • 

2.最小二乘法

令 J(θ) J ( θ ) 偏导为 0 我们可以直接求出 θ θ ， 推导过程：

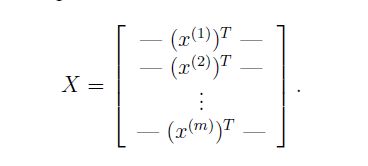
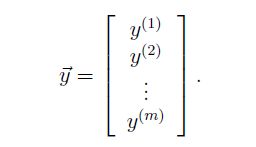
概率论解释

1.问题：

为什么在线性回归中我们要用最小二乘作为误差项，而不用三次方，四次方之类的。

2.解答：

• 设：
  
  ϵ(i) ϵ ( i ) 是误差项， ϵ(i) ϵ ( i ) ~ N(0,σ2) N ( 0 , σ 2 )

• 所以：
  
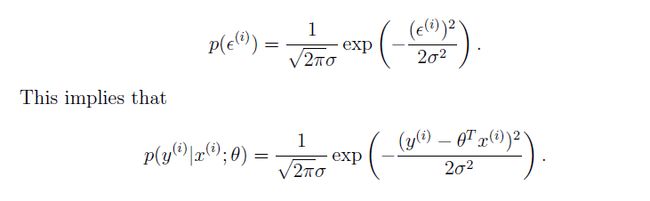
  即： y(i) y ( i ) | x(i)；θ x ( i ) ； θ ~ N(θTx(i),σ2) N ( θ T x ( i ) , σ 2 )

• 用最大概然法：
  
  

• 理解：
  我们把输入X，X = { x1,x2,x3,x4,.......,xn x 1 , x 2 , x 3 , x 4 , . . . . . . . , x n }看做一组样本，而 Y Y 是一组样本对应的观测值，而且由前面的推导我们可以知道该事件是符合 y(i) y ( i ) | x(i)；θ x ( i ) ； θ ~ N(θTx(i),σ2) N ( θ T x ( i ) , σ 2 ) 。因此利用最大似然法我们可以求出未知参数 θ θ ，即最大化 L(θ) L ( θ ) 。

  • 在梯度下降中。最大化 L(θ) L ( θ ) ，就是最小化
    
    即 J(θ) J ( θ ) ，因此我们让 J(θ) J ( θ ) 的偏导作为增量更新 θ θ ，最后 J(θ) J ( θ ) 的偏导近似为0时，我们认为迭代结束。
  • 在上面最小二乘法中。最大化 L(θ) L ( θ ) ，也就是令 l(θ) l ( θ ) 的偏导为0，因此我们可以直接求 l(θ) l ( θ ) 的偏导为0，求出 θ θ .
    

代码实现：

　　主要文件：
　　

• test1相当于主要文件
• GradientDecent主要是梯度下降更新 θ θ
• ComputeCost主要用来根据给出的 θ θ 计算出代价 J J

test1函数：

%% part0; 装载数据
data = load('ex1data1.txt');
x = data(:,1);
y = data(:,2);
m = length(y);

%%    part1: 初始化，画出离散的点
plot(x,y,'rx','Markersize',10);
ylabel('profit in $10,000s');
xlabel('population in $10,000s');
pause;

%%  part2：run gradient descent，view theta

x = [ones(m,1), data(:,1)];
theta = zeros(2,1);
iterations  = 1500;
alpha = 0.01;
computeCost(x, y, theta)
theta = gradientDescent(x, y, theta, alpha, iterations);
x2 = 4:25;
y2 = theta(1,1) + theta(2,1) * x2;
plot(x(:,2),y,'rx',x2,y2,'blu','Markersize',10);
ylabel('profit in $10,000s');
xlabel('population in $10,000s');
pause;

%% Part 4: Visualizing J(theta_0, theta_1) 

%给出相应的theta0，theta1的连续值100个，组成100*100的theta矩阵，根据每个theta组合算出cost J形成一个三维图形
%theta0， theta1， J。方便查看J的下降方向

fprintf('Visualizing J(theta_0, theta_1) ...\n')

% Grid over which we will calculate J
theta0_vals = linspace(-10, 10, 100);
theta1_vals = linspace(-1, 4, 100);

% initialize J_vals to a matrix of 0's
J_vals = zeros(length(theta0_vals), length(theta1_vals));

% Fill out J_vals
for i = 1:length(theta0_vals)
    for j = 1:length(theta1_vals)
      t = [theta0_vals(i); theta1_vals(j)];    
      J_vals(i,j) = computeCost(x, y, t);
    end
end


% Because of the way meshgrids work in the surf command, we need to 
% transpose J_vals before calling surf, or else the axes will be flipped
J_vals = J_vals';
% Surface plot
figure;
surf(theta0_vals, theta1_vals, J_vals)
xlabel('\theta_0'); ylabel('\theta_1');

% Contour plot
figure;
% Plot J_vals as 15 contours spaced logarithmically between 0.01 and 100
contour(theta0_vals, theta1_vals, J_vals, logspace(-2, 3, 20))
xlabel('\theta_0'); ylabel('\theta_1');
hold on;
plot(theta(1), theta(2), 'rx', 'MarkerSize', 10, 'LineWidth', 2);

GradientDecent函数：

function [theta,J_history] = gradientDescent(x, y, theta, alpha, num_iters)
%GRADIENTDESCENT Performs gradient descent to learn theta
%   theta = GRADIENTDESENT(X, y, theta, alpha, num_iters) updates theta by 
%   taking num_iters gradient steps with learning rate alpha

% Initialize some useful values
m = length(y); % number of training examples
J_history = zeros(num_iters, 1);
thetas = zeros(num_iters,2);

for iter = 1:num_iters

    % ====================== YOUR CODE HERE ======================
    % Instructions: Perform a single gradient step on the parameter vector
    %               theta. 
    %
    % Hint: While debugging, it can be useful to print out the values
    %       of the cost function (computeCost) and gradient here.
    %

    for j = 1:2
        dec = 0;
        for i = 1:m
            dec = dec + (x(i,:)*theta - y(i,1)) * x(i,j);
        end
        theta(j,1) = theta(j,1) - alpha*dec/m;
    end

    % ============================================================
    % Save the cost J in every iteration    
    J_history(iter) = computeCost(x, y, theta);

end
end

ComputeCost 函数：

function J = computeCost(x, y, theta)
%COMPUTECOST Compute cost for linear regression
%   J = COMPUTECOST(X, y, theta) computes the cost of using theta as the
%   parameter for linear regression to fit the data points in X and y

% Initialize some useful values
m = length(y); % number of training examples

% You need to return the following variables correctly 
J = 0;
% ====================== YOUR CODE HERE ======================
% Instructions: Compute the cost of a particular choice of theta
%               You should set J to the cost.
for i=1 : m
    J = J + (y(i,:)- x(i,:)*theta)^2;
end

J = J /(2*m);

% =========================================================================

end

代码

百度云下载

---

其它平台只是信息转发(留言可能看不到)，欢迎同学们到个人blog交流：https://faiculty.com/