scikit-learn官方文档-preprocessing data(数据预处理)

一、标准化，均值和方差缩放

数据集的标准化是许多在scikit-learn中实现的机器学习估计器的普遍要求。如果单个特征或多或少看起来不像标准正态分布数据，则它们的性能可能会很差。标准正态分布的定义：平均值和单位方差为零的高斯。
在实践中，我们经常忽略分布的形状，而只是通过删除每个特征的平均值来变换数据以使其居中，然后通过将非恒定特征除以它们的标准偏差来缩放它。
例如，学习算法的目标函数中使用的许多元素（例如支持向量机的RBF内核或线性模型的l1和l2正则化器）都假定所有特征都围绕零为中心并且具有相同顺序的方差。如果某个特征的方差比其他特征大几个数量级，则它可能会支配目标函数并使估计器无法按预期从其他特征中正确学习。
函数scale提供了一种快速简便的方法来对单个类似数组的数据集执行此操作:

>>> from sklearn import preprocessing
>>> import numpy as np
>>> X_train = np.array([[ 1., -1.,  2.],
...                     [ 2.,  0.,  0.],
...                     [ 0.,  1., -1.]])
>>> X_scaled = preprocessing.scale(X_train)

>>> X_scaled
array([[ 0.  ..., -1.22...,  1.33...],
       [ 1.22...,  0.  ..., -0.26...],
       [-1.22...,  1.22..., -1.06...]])

标度后数据的均值和单位方差为零

>>> X_scaled.mean(axis=0)
array([0., 0., 0.])

>>> X_scaled.std(axis=0)
array([1., 1., 1.])

预处理模块还提供了一个实用程序类StandardScaler，该类实现Transformer API以计算训练集上的均值和标准差，以便以后可以在测试集上重新应用相同的变换。因此，此类适合在sklearn.pipeline.Pipeline的早期步骤中使用：

>>> scaler = preprocessing.StandardScaler().fit(X_train)
>>> scaler
StandardScaler()

>>> scaler.mean_
array([1. ..., 0. ..., 0.33...])

>>> scaler.scale_
array([0.81..., 0.81..., 1.24...])

>>> scaler.transform(X_train)
array([[ 0.  ..., -1.22...,  1.33...],
       [ 1.22...,  0.  ..., -0.26...],
       [-1.22...,  1.22..., -1.06...]])

然后可以将缩放器实例用于新数据，以与训练集相同的方式对其进行转换：

>>> X_test = [[-1., 1., 0.]]
>>> scaler.transform(X_test)
array([[-2.44...,  1.22..., -0.26...]])

通过将with_mean = False或with_std = False传递给StandardScaler的构造函数，可以禁用居中或缩放。

1、缩放特征

另一种标准化方法是将特征缩放到给定的最小值和最大值之间，通常介于零和一之间，或者将每个特征的最大绝对值缩放到单位大小。这可以分别使用MinMaxScaler或MaxAbsScaler来实现。
使用这种缩放的动机包括对特征的很小标准偏差的鲁棒性以及在稀疏数据中保留零项。
这是将数据矩阵缩放到[0，1]范围的示例：

>>> X_train = np.array([[ 1., -1.,  2.],
...                     [ 2.,  0.,  0.],
...                     [ 0.,  1., -1.]])
...
>>> min_max_scaler = preprocessing.MinMaxScaler()
>>> X_train_minmax = min_max_scaler.fit_transform(X_train)
>>> X_train_minmax
array([[0.5       , 0.        , 1.        ],
       [1.        , 0.5       , 0.33333333],
       [0.        , 1.        , 0.        ]])

然后可以将变压器的相同实例应用于拟合调用期间未看到的一些新测试数据：将应用相同的缩放和移位操作，以与对训练数据执行的转换一致：

>>> X_test = np.array([[-3., -1.,  4.]])
>>> X_test_minmax = min_max_scaler.transform(X_test)
>>> X_test_minmax
array([[-1.5       ,  0.        ,  1.66666667]])

可以对缩放器属性进行内部检查，以找到在训练数据上学习到的转换的确切性质：

>>> min_max_scaler.scale_
array([0.5       , 0.5       , 0.33...])

>>> min_max_scaler.min_
array([0.        , 0.5       , 0.33...])

如果给MinMaxScaler一个明确的feature_range =（min，max），则完整公式为：

X_std = (X - X.min(axis=0)) / (X.max(axis=0) - X.min(axis=0))

X_scaled = X_std * (max - min) + min

MaxAbsScaler的工作方式非常相似，但通过除以每个特征中的最大值来将训练数据置于[-1，1]范围内。它适用于已经以零或稀疏数据为中心的数据。
这是在此缩放器上使用上一示例中的数据的方法：

>>> X_train = np.array([[ 1., -1.,  2.],
...                     [ 2.,  0.,  0.],
...                     [ 0.,  1., -1.]])
...
>>> max_abs_scaler = preprocessing.MaxAbsScaler()
>>> X_train_maxabs = max_abs_scaler.fit_transform(X_train)
>>> X_train_maxabs
array([[ 0.5, -1. ,  1. ],
       [ 1. ,  0. ,  0. ],
       [ 0. ,  1. , -0.5]])
>>> X_test = np.array([[ -3., -1.,  4.]])
>>> X_test_maxabs = max_abs_scaler.transform(X_test)
>>> X_test_maxabs
array([[-1.5, -1. ,  2. ]])
>>> max_abs_scaler.scale_
array([2.,  1.,  2.])

与scale一样，如果您不想创建对象，该模块还将提供便捷功能minmax_scale和maxabs_scale。

2、缩放稀疏数据

将稀疏数据居中会破坏数据中的稀疏结构，因此会是很少要做的敏感的操作。但是，缩放稀疏输入是有意义的，尤其是在要素处于不同缩放比例时。
MaxAbsScaler和maxabs_scale是专门为缩放稀疏数据而设计的，是实现此目的的推荐方法。但是，scale和StandardScaler可以接受scipy.sparse矩阵作为输入，只要with_mean = False显式传递给构造函数即可。否则，将引发ValueError，因为静默居中会破坏稀疏性，并经常由于无意中分配过多的内存而使执行崩溃。 RobustScaler无法适合稀疏输入，但是您可以对稀疏输入使用transform方法。
请注意，缩放器接受压缩的稀疏行和压缩的稀疏列格式（请参见scipy.sparse.csr_matrix和scipy.sparse.csc_matrix）。任何其他稀疏输入都将转换为“压缩稀疏行”表示形式。为避免不必要的内存复制，建议选择上游的CSR或CSC表示形式。
最后，如果期望居中的数据足够小，则使用稀疏矩阵的toarray方法将输入显式转换为数组是另一种选择。

3、使用离群值扩展数据

如果您的数据包含许多离群值，则使用数据的均值和方差进行缩放可能效果不佳。在这些情况下，您可以改为使用robust_scale和RobustScaler作为替代产品。他们对数据的中心和范围使用更可靠的估计。

Scaling vs Whitening

有时仅靠集中中心和缩放特征是不够的，因为下游模型可以进一步假设特征的线性独立性。

要解决此问题，您可以将sklearn.decomposition.PCA与whiten = True一起使用，以进一步消除跨要素的线性相关性。

4、居中核矩阵

如果您有一个内核为K的内核矩阵，可以在函数定义的特征空间中计算点积，则KernelCenterer可以转换内核矩阵，以使其包含特征空间中的内积，然后在该空间中去除均值。

二、非线性变化

有两种类型的转换：分位数转换和幂转换。分位数和幂变换都基于特征的单调变换，因此保留了沿每个特征的值的等级。
分位数变换根据公式G^-1(F(x))将所有特征置于相同的期望分布中，其中F是特征的累积分布函数,G -1是期望输出分布的分位数函数。该公式利用了以下两个事实：（i）如果X是具有连续累积分布函数F的随机变量，则F(x)均匀地分布在[0,1];（ii）如果U随机变量且在[0,1]具有均匀分布，则G-1(U)具有分布G。通过执行秩变换，分位数变换可以平滑不寻常的分布，并且与缩放方法相比，离群值的影响较小。但是，它确实扭曲了要素内部和要素之间的相关性和距离。
幂变换是一组参数变换，旨在将数据从任何分布映射到接近高斯分布。

1、映射到一个统一分布

QuantileTransformer和Quantile_transform提供了一种非参数转换，可以将数据映射到值在0和1之间的均匀分布：

>>> from sklearn.datasets import load_iris
>>> from sklearn.model_selection import train_test_split
>>> X, y = load_iris(return_X_y=True)
>>> X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)
>>> quantile_transformer = preprocessing.QuantileTransformer(random_state=0)
>>> X_train_trans = quantile_transformer.fit_transform(X_train)
>>> X_test_trans = quantile_transformer.transform(X_test)
>>> np.percentile(X_train[:, 0], [0, 25, 50, 75, 100]) 
array([ 4.3,  5.1,  5.8,  6.5,  7.9])

此特征对应于以厘米为单位的萼片长度。一旦应用了分位数转换，这些界标就会接近先前定义的百分位数：

>>> np.percentile(X_train_trans[:, 0], [0, 25, 50, 75, 100])
... 
array([ 0.00... ,  0.24...,  0.49...,  0.73...,  0.99... ])

可以在具有类似说明的独立测试仪上对此进行确认：

>>> np.percentile(X_test[:, 0], [0, 25, 50, 75, 100])
... 
array([ 4.4  ,  5.125,  5.75 ,  6.175,  7.3  ])
>>> np.percentile(X_test_trans[:, 0], [0, 25, 50, 75, 100])
... 
array([ 0.01...,  0.25...,  0.46...,  0.60... ,  0.94...])

2、映射到一个高斯分布

在许多建模方案中，需要数据集中要素的正态性。幂变换是一组参数化，单调变换，旨在将数据从任何分布映射到尽可能接近高斯分布的位置，以稳定方差并使偏斜最小化。
PowerTransformer当前提供两种这样的功率变换，即Yeo-Johnson变换和Box-Cox变换。

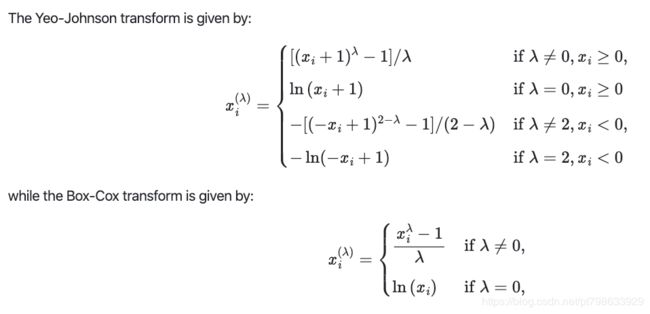
Box-Cox仅可应用于严格的正数据。在这两种方法中，变换均通过lambda进行参数化，通过最大似然估计来确定。这有一个使用Box-Cox将从对数正态分布绘制的样本映射到正态分布的示例：

>>> pt = preprocessing.PowerTransformer(method='box-cox', standardize=False)
>>> X_lognormal = np.random.RandomState(616).lognormal(size=(3, 3))
>>> X_lognormal
array([[1.28..., 1.18..., 0.84...],
       [0.94..., 1.60..., 0.38...],
       [1.35..., 0.21..., 1.09...]])
>>> pt.fit_transform(X_lognormal)
array([[ 0.49...,  0.17..., -0.15...],
       [-0.05...,  0.58..., -0.57...],
       [ 0.69..., -0.84...,  0.10...]])

虽然上面的示例将standardize选项设置为False，但是PowerTransformer默认将零均值，单位方差归一化应用于转换后的输出。
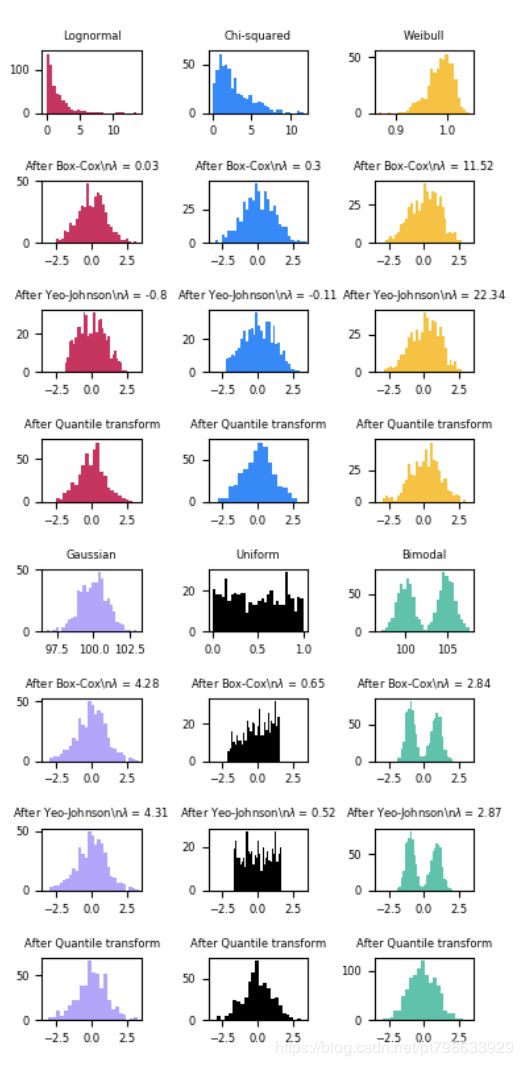
以下是适用于各种概率分布的Box-Cox和Yeo-Johnson的示例。请注意，当将功率变换应用于某些分布时，它们会获得非常类似于高斯的结果，但是对于其他结果，它们是无效的。这突出了在转换之前和之后可视化数据的重要性。

也可以使用Quantile Transformer通过设置ouput_distribution='normal’将数据映射到正态分布，以Iris数据集为例：

>>> quantile_transformer = preprocessing.QuantileTransformer(
...     output_distribution='normal', random_state=0)
>>> X_trans = quantile_transformer.fit_transform(X)
>>> quantile_transformer.quantiles_
array([[4.3, 2. , 1. , 0.1],
       [4.4, 2.2, 1.1, 0.1],
       [4.4, 2.2, 1.2, 0.1],
       ...,
       [7.7, 4.1, 6.7, 2.5],
       [7.7, 4.2, 6.7, 2.5],
       [7.9, 4.4, 6.9, 2.5]])

因此，输入的中位数成为以0为中心的输出的平均值。正常输出被裁剪，以便输入的最小和最大值（分别对应于1e-7和1-1e-7分位数）在以下条件下不会变为无限大转型。

三、正态化

标准化是将单个样本缩放为具有单位范数的过程。如果计划使用点积或任何其他核的二次形式来量化任意一对样本的相似性，则此过程可能会很有用。
该假设是向量空间模型的基础，该向量空间模型经常用于文本分类和聚类上下文中。
函数规范化提供了一种快速简便的方法，可以使用l1或l2规范对单个数组状数据集执行此操作：

>>> X = [[ 1., -1.,  2.],
...      [ 2.,  0.,  0.],
...      [ 0.,  1., -1.]]
>>> X_normalized = preprocessing.normalize(X, norm='l2')

>>> X_normalized
array([[ 0.40..., -0.40...,  0.81...],
       [ 1.  ...,  0.  ...,  0.  ...],
       [ 0.  ...,  0.70..., -0.70...]])

预处理模块还提供了一个实用程序类Normalizer，该类使用Transformer API实现相同的操作（即使fit方法在这种情况下也没有用：该类是无状态的，因为此操作独立地处理样本）。
因此，此类适合在sklearn.pipeline.Pipeline的早期步骤中使用：

>>> normalizer = preprocessing.Normalizer().fit(X)  # fit does nothing
>>> normalizer
Normalizer()

然后，可以将normalizer实例用作任何转换器的样本矢量：

>>> normalizer.transform(X)
array([[ 0.40..., -0.40...,  0.81...],
       [ 1.  ...,  0.  ...,  0.  ...],
       [ 0.  ...,  0.70..., -0.70...]])

>>> normalizer.transform([[-1.,  1., 0.]])
array([[-0.70...,  0.70...,  0.  ...]])

注意：L2归一化也称为空间符号预处理。

四、编码类别向量

通常，功能不是连续值而是分类的。例如，一个人可能具有特征[“男性”，“女性”]，[“来自欧洲”，“来自美国”，“来自亚洲”]，[“使用Firefox”，“使用Chrome”，“使用Safari”，“使用Internet Explorer”]。这样的功能可以有效地编码为整数，例如[[male]，“来自美国”，“使用Internet Explorer”]可以表示为[0，1，3]，而[“ female”，“来自亚洲”，“使用Chrome“]为[1、2、1]。
要将分类特征转换为此类整数代码，我们可以使用OrdinalEncoder。此估算器将每个分类特征转换为一个整数（0到n_categories-1）的新特征：

>>> enc = preprocessing.OrdinalEncoder()
>>> X = [['male', 'from US', 'uses Safari'], ['female', 'from Europe', 'uses Firefox']]
>>> enc.fit(X)
OrdinalEncoder()
>>> enc.transform([['female', 'from US', 'uses Safari']])
array([[0., 1., 1.]])

但是，此类整数表示不能直接与所有scikit-learn估计器一起使用，因为它们期望连续输入，并且会将类别解释为有序的，这通常是不希望的（例如：浏览器集是任意定序的）。
将分类特征转换为可以与scikit-learn估计器一起使用的特征的另一种可能性是使用K的一，也称为单热或伪编码。可以使用OneHotEncoder获得这种类型的编码，该编码器将具有n_categories个可能值的每个分类特征转换为n_categories个二进制特征，其中一个为1，所有其他为0。
继续上述的例子：

>>> enc = preprocessing.OneHotEncoder()
>>> X = [['male', 'from US', 'uses Safari'], ['female', 'from Europe', 'uses Firefox']]
>>> enc.fit(X)
OneHotEncoder()
>>> enc.transform([['female', 'from US', 'uses Safari'],
...                ['male', 'from Europe', 'uses Safari']]).toarray()
array([[1., 0., 0., 1., 0., 1.],
       [0., 1., 1., 0., 0., 1.]])

默认情况下，每个功能可以采用的值是从数据集中自动推断出的，并且可以在Categories_属性中找到：

>>> enc.categories_
[array(['female', 'male'], dtype=object), array(['from Europe', 'from US'], dtype=object), array(['uses Firefox', 'uses Safari'], dtype=object)]

可以使用参数类别明确指定。我们的数据集中有两种性别，四个可能的大洲和四个网络浏览器：

>>> genders = ['female', 'male']
>>> locations = ['from Africa', 'from Asia', 'from Europe', 'from US']
>>> browsers = ['uses Chrome', 'uses Firefox', 'uses IE', 'uses Safari']
>>> enc = preprocessing.OneHotEncoder(categories=[genders, locations, browsers])
>>> # Note that for there are missing categorical values for the 2nd and 3rd
>>> # feature
>>> X = [['male', 'from US', 'uses Safari'], ['female', 'from Europe', 'uses Firefox']]
>>> enc.fit(X)
OneHotEncoder(categories=[['female', 'male'],
                          ['from Africa', 'from Asia', 'from Europe',
                           'from US'],
                          ['uses Chrome', 'uses Firefox', 'uses IE',
                           'uses Safari']])
>>> enc.transform([['female', 'from Asia', 'uses Chrome']]).toarray()
array([[1., 0., 0., 1., 0., 0., 1., 0., 0., 0.]])

如果训练数据有可能缺少分类特征，则通常最好指定handle_unknown =‘ignore’，而不是如上所述手动设置类别。当指定handle_unknown ='ignore’且在转换过程中遇到未知类别时，不会引发错误，但此功能生成的一键编码列将全为零（handle_unknown ='ignore’仅支持一键编码）：

>>> enc = preprocessing.OneHotEncoder(handle_unknown='ignore')
>>> X = [['male', 'from US', 'uses Safari'], ['female', 'from Europe', 'uses Firefox']]
>>> enc.fit(X)
OneHotEncoder(handle_unknown='ignore')
>>> enc.transform([['female', 'from Asia', 'uses Chrome']]).toarray()
array([[1., 0., 0., 0., 0., 0.]])

也可以使用drop参数将每一列编码为n_categories-1列而不是n_categories列。该参数允许用户为每个要删除的功能指定一个类别。在某些分类器中，这有助于避免输入矩阵中的共线性。例如，当使用非正则回归（LinearRegression）时，此类功能很有用，因为共线性会导致协方差矩阵不可逆。当此参数不是None时，必须将handle_unknown设置为error：

>>> X = [['male', 'from US', 'uses Safari'], ['female', 'from Europe', 'uses Firefox']]
>>> drop_enc = preprocessing.OneHotEncoder(drop='first').fit(X)
>>> drop_enc.categories_
[array(['female', 'male'], dtype=object), array(['from Europe', 'from US'], dtype=object), array(['uses Firefox', 'uses Safari'], dtype=object)]
>>> drop_enc.transform(X).toarray()
array([[1., 1., 1.],
       [0., 0., 0.]])

五、离散化

离散化（也称为量化或合并）提供了一种将连续特征划分为离散值的方法。某些具有连续特征的数据集可能会受益于离散化，因为离散化可以将连续属性的数据集转换为仅具有名义属性的数据集。
一键编码的离散特征可以使模型更具表现力，同时保持可解释性。例如，使用离散器的预处理可以将非线性引入线性模型。
1、K-bins离散化
KBinsDiscretizer将特征离散到k个bin中：

>>> X = np.array([[ -3., 5., 15 ],
...               [  0., 6., 14 ],
...               [  6., 3., 11 ]])
>>> est = preprocessing.KBinsDiscretizer(n_bins=[3, 2, 2], encode='ordinal').fit(X)

默认情况下，输出是单次热编码到稀疏矩阵中的（请参阅编码分类功能），并且可以使用encode参数进行配置。对于每个特征，将在拟合过程中计算仓边，并与仓数一起定义间隔。因此，对于当前示例，这些间隔定义为：

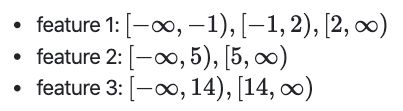
基于这些bin间隔，X转换如下：

>>> est.transform(X)                      
array([[ 0., 1., 1.],
       [ 1., 1., 1.],
       [ 2., 0., 0.]])

结果数据集包含序数属性，这些序数属性可以在sklearn.pipeline.Pipeline中进一步使用。
离散化类似于构造连续数据的直方图。但是，直方图着重于对落入特定区域的特征进行计数，而离散化则着重于为这些区域分配特征值。
KBinsDiscretizer实现不同的装箱策略，可以通过strategy参数进行选择。 “统一”策略使用固定宽度的垃圾箱。 “分位数”策略使用分位数值在每个要素中具有均等填充的bin。 “ kmeans”策略基于对每个要素独立执行的k均值聚类过程来定义区域。
2、特征二值化
特征二值化是对数字特征进行阈值化以获得布尔值的过程。这对于下游概率估计器很有用，这些估计器假设输入数据是根据多元Bernoulli分布进行分布的。例如，sklearn.neural_network.BernoulliRBM就是这种情况。
在文本处理社区中，即使在实践中通常使用归一化计数（即术语频率）或TF-IDF值化的功能通常表现稍佳的情况，也使用二进制特征值（可能是为了简化概率推理）。
至于Normalizer，实用程序Binarizer类打算在sklearn.pipeline.Pipeline的早期阶段使用。由于每个样品都独立对待，因此fit方法无济于事：

>>> X = [[ 1., -1.,  2.],
...      [ 2.,  0.,  0.],
...      [ 0.,  1., -1.]]

>>> binarizer = preprocessing.Binarizer().fit(X)  # fit does nothing
>>> binarizer
Binarizer()

>>> binarizer.transform(X)
array([[1., 0., 1.],
       [1., 0., 0.],
       [0., 1., 0.]])

可以调整二值化器的阈值：

>>> binarizer = preprocessing.Binarizer(threshold=1.1)
>>> binarizer.transform(X)
array([[0., 0., 1.],
       [1., 0., 0.],
       [0., 0., 0.]])

对于StandardScaler和Normalizer类，预处理模块提供了一个配套函数二值化，可在不需要变换器API时使用。
请注意，当k = 2且bin边缘处于值阈值时，Binarizer与KBinsDiscretizer相似。

六、估算缺失值

七、生成多项式特征

通常，考虑输入数据的非线性特征会增加模型的复杂性。多项式特征是一种简单而常用的方法，它可以获取特征的高阶和相互作用项。它在PolynomialFeatures中实现：

>>> import numpy as np
>>> from sklearn.preprocessing import PolynomialFeatures
>>> X = np.arange(6).reshape(3, 2)
>>> X
array([[0, 1],
       [2, 3],
       [4, 5]])
>>> poly = PolynomialFeatures(2)
>>> poly.fit_transform(X)
array([[ 1.,  0.,  1.,  0.,  0.,  1.],
       [ 1.,  2.,  3.,  4.,  6.,  9.],
       [ 1.,  4.,  5., 16., 20., 25.]])

X的特征从（X1，X2）转换成了（1，X1，X2，X1^2，X1，X2，X2平方）
在某些情况下，仅需要要素之间的交互项，并且可以通过设置interact_only = True来获得：

>>> X = np.arange(9).reshape(3, 3)
>>> X
array([[0, 1, 2],
       [3, 4, 5],
       [6, 7, 8]])
>>> poly = PolynomialFeatures(degree=3, interaction_only=True)
>>> poly.fit_transform(X)
array([[  1.,   0.,   1.,   2.,   0.,   0.,   2.,   0.],
       [  1.,   3.,   4.,   5.,  12.,  15.,  20.,  60.],
       [  1.,   6.,   7.,   8.,  42.,  48.,  56., 336.]])

X的特征从(X1,X2,X3)转换到了(1,X1,X2,X3,X1X2,X1X3,X2X3,X1X2X3)
请注意，使用多项式内核函数时，多项式特征在内核方法（例如sklearn.svm.SVC，sklearn.decomposition.KernelPCA）中隐式使用。
有关使用创建的多项式特征的Ridge回归的信息，请参见多项式插值。

八、定制转化器

通常，您将需要将现有的Python函数转换为转换器，以帮助进行数据清理或处理。您可以使用FunctionTransformer从任意函数中实现转换器。例如，要构建在管道中应用对数转换的转换器，请执行以下操作：

>>> import numpy as np
>>> from sklearn.preprocessing import FunctionTransformer
>>> transformer = FunctionTransformer(np.log1p, validate=True)
>>> X = np.array([[0, 1], [2, 3]])
>>> transformer.transform(X)
array([[0.        , 0.69314718],
       [1.09861229, 1.38629436]])

您可以通过设置check_inverse = True并在变换之前调用fit来确保func和inverse_func彼此相反。请注意，将发出警告，并可能通过过滤警告变为错误：

>>> import warnings
>>> warnings.filterwarnings("error", message=".*check_inverse*.",
...                         category=UserWarning, append=False)

有关演示如何使用FunctionTransformer进行自定义功能选择的完整代码示例，请参见使用FunctionTransformer选择列