玩转数据结构——第七章:优先队列和堆
内容概要:
- 什么是优先队列?
- 堆的基础结构
- 向堆中添加元素Sift Up
- 从堆中取出元素和Sift Down
- Heapify和Replace
- 基于堆的优先队列
- LeetCode上优先队列相关的问题
- java中的PriorityQueue
- 和堆相关的更多话题和广义队列
一、什么是优先队列?
不同树的数据结构四种例子:
- 堆
- 线段树
- 字典树
- 并查集
- 什么是优先队列?
普通队列:先进先出,后进后出
优先队列:出队顺序和入队顺序无关;和优先级相关
例子:比如去看病,患者需要排队挂号,但有严重患者人来时,它可以提前进入看病。(这就是根据病的紧急情况来决定的)
- 为什么要使用优先队列呢?
动态选择优先级最高的任务执行
动态:不能够一开始就确定需要处理多少任务,它需要根据新来的任务来重新进行优先级排序,优先级高的先执行
优先队列的实现:
| 入队 | 出队(拿出最大元素) | |
| 线性结构 | ||
| 顺序线性结构 | ||
| 堆 |
二、堆(Heap)的基础结构
当时间复杂度为![]() 时,一般都是树结构
时,一般都是树结构
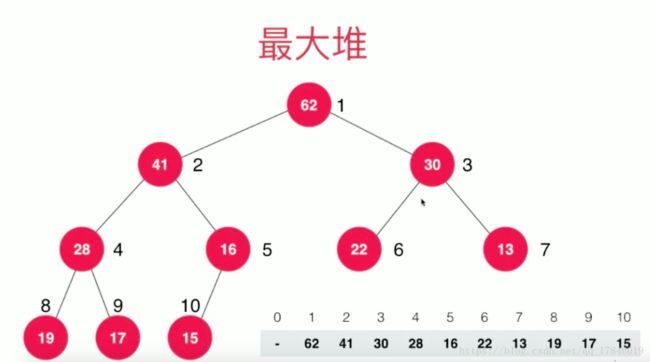
二叉堆:是一个完全二叉树
- 满二叉树 :
除了叶子节点,所有的节点都有左右孩子
- 完全二叉树:
把元素排列成树的形状(一层一层的排,排完到下一层,从左到右排,它存在的叶子节点集中在右边)
二叉堆的性质
- 堆中某个节点的值总是不大于其父亲节点(根节点是最大的元素,大于它左右节点的值)
- 最大堆(相对于可以定义最小堆),每个元素的节点,小于其左右孩子的节点值
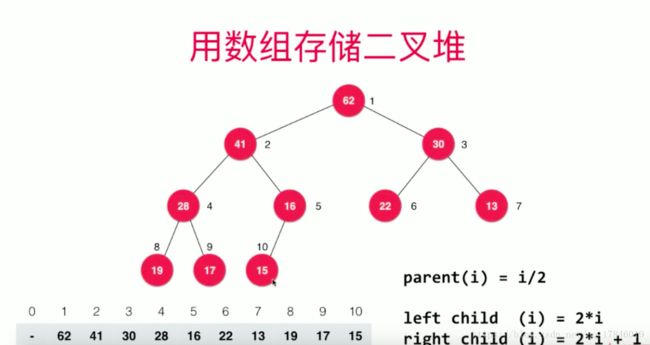
如果数组索引为0空出来:
parent(i)=i/2;//父亲节点
left child(i)=2*i;//该节点左孩子的索引
right child(i)=2*i+1; //该节点右孩子索引如果索引为0不空出来
parent(i)=(i-1)/2;//父亲节点 int整形除3/2为1
left child(i)=2*i+1;//该节点左孩子的索引
right child(i)=2*i+2; //该节点右孩子索引最大堆的实现:基于动态数组实现的最大堆MaxHeap的基础操作
//元素可比较性
public class MaxHeap> {
private Array data;//动态数组
//如果传入容量
public MaxHeap(int capacity) {
data = new Array<>(capacity);//初始化动态数组
}
public MaxHeap() {
data = new Array<>();
}
//返回堆中的元素个数
public int size() {
return data.getSize();
}
//返回一个布尔值,表示堆中是否为空
public boolean isEmpty() {
return data.isEmpty();
}
} 辅助函数:找一个节点的父亲节点、左孩子节点、右孩子节点的索引
//辅助函数
//返回完全二叉树的数组表示中,一个索引所表示的元素的父亲节点的索引
public int parent(int index) {
if (index == 0)
throw new IllegalArgumentException("index-0 doesn't have parent");
return (index - 1) / 2;
}
//返回完全二叉树的数组表示中,一个索引所表示的元素的左孩子节点的索引
public int leftChild(int index) {
return (index * 2 + 1);
}
//返回完全二叉树的数组表示中,一个索引所表示的元素的右孩子节点的索引
public int rightChild(int index) {
return index * 2 + 2;
}
三、向堆中添加元素Sift Up//上浮
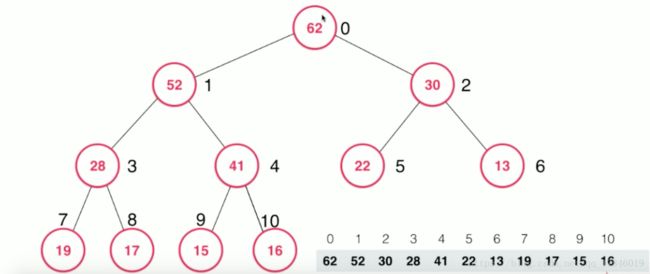
新添加的元素52,不再满足堆的特性:节点的值大于左右孩子节点的值,那该怎么办?
出现问题的是52这个节点,那就可以一层一层的找它的父亲节点和它的父亲节点做比较,然后交换这两个元素的位置
//在自定义Array动态数组的类中添加
//元素交换
public void swap(int i, int j) {
if (i < 0 || i >= size || j < 0 || j >= size)
throw new IllegalArgumentException("Index is Illegal");
E t = data[i];
data[i] = data[j];
data[j] = t;
}向堆中添加元素siftUp:
//上浮操作,传入你要上浮元素的index
private void siftUp(int k){
//不能达到根节点 k所在元素和它的父亲节点做比较,如果大于父亲节点的话就要交换位置
while (k>0 && data.get(parent(k)).compareTo(data.get(k))<0){
data.swap(k,parent(k));//交换元素的值
k=parent(k);//新的位置
}
}四、从堆中取出元素和Sift Down(下沉)
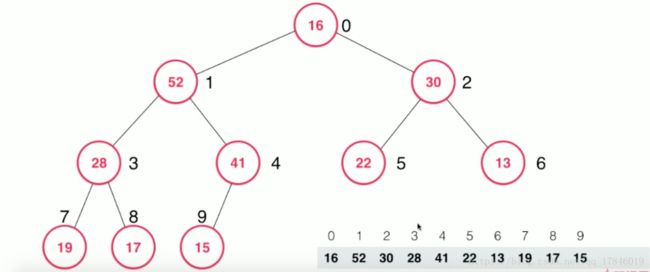
从最大堆中取出元素,即取出最大的元素,末尾的元素给顶到最大堆原来的位置
然后看末尾元素是否满足大于左右子树,不满足而与其最大交换位置(称为下沉操作)
直到最终满足完全二叉树和大于左右子树值的特性。
//寻找堆的最大值
public E findMax() {
if (data.get(0) == null)//如果最大值不存在,空堆
throw new IllegalArgumentException("cnt not findMax when heap is empty!");
return data.get(0);
}
//取出堆的最大元素并删除
public E extractMax() {
E ret = findMax();
data.swap(0, data.getSize() - 1);//最大值和最末尾的元素进行交换
//下沉操作
siftDown(0);
return ret;
}
//下沉操作,传入需要下沉的index
public void siftDown(int k) {
while (leftChild(k) < data.getSize()) {//当索引k越界的时候循环结束(达到叶子节点的之下)
int j = leftChild(k);//将它的左孩子索引存起来//一定有左孩子,但不一定有右孩子
//如果它存在右孩子,并且右孩子的值大于左孩子
if (rightChild(k) < data.getSize() && data.get(rightChild(k)).compareTo(data.get(leftChild(k))) > 0) {
j = rightChild(k);//j+1;
}
//data[j]是leftChild和rightChild中的最大值
if (data.get(k).compareTo(data.get(j)) > 0)//父亲节点大于它左右孩子中最大值
break;//退出循环
//否则交换它们的值
data.swap(j, k);
k = j;//最终k的索引变成j,进行下轮循环,看是否需要再次下沉
}
}测试:实现用最大堆进行数组从大到小的排序
/***
* 用最大堆实现元素排序(从大到小)
*/
public class Main {
public static void main(String[] args) {
int n = 10;//一个随机数
MaxHeap maxHeap = new MaxHeap<>();
Random random = new Random();
for (int i = 0; i < n; i++)
maxHeap.add(random.nextInt(Integer.MAX_VALUE));//从0到Integer的最大值
//创建一个数组每次从堆中取出最大元素放进去(实现从大到小的排序)
int[] arr = new int[n];
for (int i = 0; i < n; i++)
arr[i] = maxHeap.extractMax();
System.out.println(Arrays.toString(arr));//打印这个数组
}
}
结果:
[1442712010, 1147348309, 822146177, 783463526, 594504611, 474708347, 394368000, 221767976, 196769889, 96631889]
堆的时间复杂度:
add和extractMax时间复杂度都是O(logn),和二叉树的高度有个
一个完全二叉树是不可能退化成链表
五、Heapify和Replace
Replace
取出最大元素后,放入一个新的元素。
- 实现:可以先 extraMax,再 add,两次 O(logn)的操作
- 实现:可以直接将堆顶元素替换以后 Sift Down,一次 O(logn)的操作
代码演示
// 取出堆中的最大元素,并且替换成元素 e
public E replace(E e){
E ret = findMax();
data.set(0, e);
siftDown(0);
return ret;
}Heapify
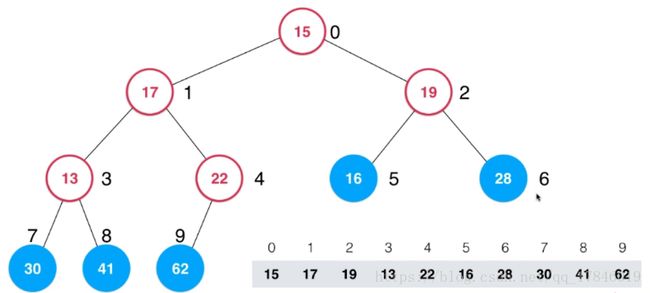
将任意数组整理成堆的形状。将当前数组看成一个完全二叉树,这个例子中,对于这个数组并不是一个堆,不满足堆的性质。
但是我们同样可以把它看成一棵完全二叉树,对于这个完全二叉树,我们从最后一个非叶子节点开始计算,如下图所示有五个叶子节点:
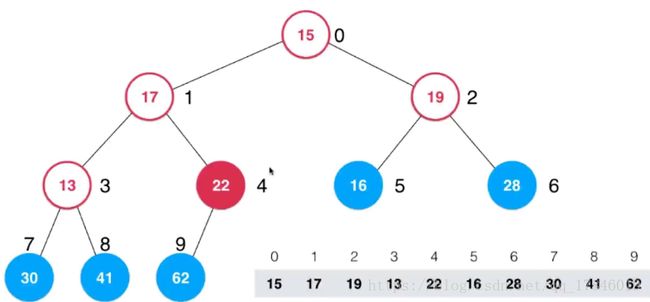
最后一个非叶子节点就是 22 这个元素所在的节点,从这个节点开始倒着从后向前不断的 Sift Down 就可以了。
首先由一个非常重要的问题,就是我们如何定位最后一个非叶子节点所处的索引是多少?
- 从最后一个非叶子节点开始计算(如何获得节点?答:拿到最后一个节点,然后拿到他的父亲节点)
- 比如最后一个节点size-1,name它的父亲节点(最后一个非叶子节点)为:parent(size-1)
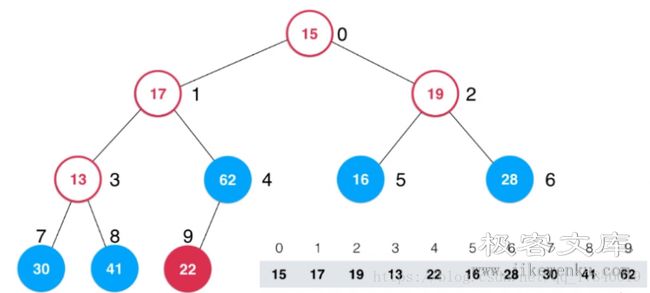
找到它父亲节点,接下来就进行 Sift Down 操作,22 和 62 交换,此时 22 已经是叶子节点了,下沉操作就完成了。
然后看索引为 3 的节点,13 和 41 交换,13 变成叶子节点无法继续下沉。
然后接下来依次类推,最终结果如下,建议仔细分析一下操作流程。
这是整个流程图:
Heapify 的算法复杂度
不使用Heapify的过程:将 n 个元素逐个插入到一个空堆中,算法复杂度是 O(nlogn)
使用 Heapify 的过程,算法复杂度为 O(n)
当n>10时,O(nlogn)>O(n)
代码演示
//不带参的构造,默认没有使用Heapify
public MaxHeap(){
data = new Array<>();
}
//带参构造,使用Heapify
public MaxHeap(E[] arr){
data = new Array<>(arr);
for(int i = parent(arr.length - 1) ; i >= 0 ; i --)//从最后一个非叶子节点开始siftDown
siftDown(i);
}在 Array.java 中添加一个新的构造函数
//带参构造将一个数组转成动态数组
public Array(E[] arr){
data = (E[])new Object[arr.length];
for(int i = 0 ; i < arr.length ; i ++)
data[i] = arr[i];
size = arr.length;
}Main.java 中编写一个测试函数
private static double testHeap(Integer[] testData, boolean isHeapify){
long startTime = System.nanoTime();
MaxHeap maxHeap;
if(isHeapify)//使用Heapify插入元素
maxHeap = new MaxHeap<>(testData);
else{//不使用Heapify插入元素
maxHeap = new MaxHeap<>();
for(int num: testData)
maxHeap.add(num);
}
//取出元素的操作
int[] arr = new int[testData.length];
for(int i = 0 ; i < testData.length ; i ++)
arr[i] = maxHeap.extractMax();
for(int i = 1 ; i < testData.length ; i ++)
if(arr[i-1] < arr[i])
throw new IllegalArgumentException("Error");
System.out.println("Test MaxHeap completed.");
long endTime = System.nanoTime();
return (endTime - startTime) / 1000000000.0;
} 下面测试一下,还是用上一节的测试用例
public static void main(String[] args) {
int n = 1000000;
Random random = new Random();
Integer[] testData = new Integer[n];
for(int i = 0 ; i < n ; i ++)
testData[i] = random.nextInt(Integer.MAX_VALUE);
double time1 = testHeap(testData, false);
System.out.println("Without heapify: " + time1 + " s");
double time2 = testHeap(testData, true);
System.out.println("With heapify: " + time2 + " s");
}
最终的运行结果如下
Test MaxHeap completed.
Without heapify: 1.591017607 s
Test MaxHeap completed.
With heapify: 1.387019963 s在我的电脑上,对于一百万的数据量,如果不使用 Heapify 操作的话时间是 1.59秒,如果使用 Heapify 的话时间是 1.38 秒。
六、基于堆的优先队列
如果想实现按照自己的意愿进行优先级排列的队列的话,需要实现Comparator接口。如果不提供Comparator的话,优先队列中元素默认按自然顺序排列,也就是数字默认是小的在队列头,字符串则按字典序排列。
/**
* 基于最大堆实现优先队列
* @param
*/
public class PriorityQueue> implements Queue {
private MaxHeap maxHeap;
public PriorityQueue(){
maxHeap=new MaxHeap<>();
}
@Override
public int getSize(){
return maxHeap.size();
}
@Override
public boolean isEmpty(){
return maxHeap.isEmpty();
}
@Override
public E getFront(){
return maxHeap.findMax();//第一个元素是最大的
}
@Override
public void enqueue(E e){
maxHeap.add(e);
}
@Override
public E dequeue(){
return maxHeap.extractMax();//删除最大值
}
} 七、优先队列的经典问题:
在 100 0000个元素中选出前100名?
在N个元素总选出前M个元素(N>>M)
如果使用排序的时间复杂度O(NlogN)
使用优先队列——>O(NlogM)
使用一个优先队列,维护当前看到的前M个元素。
Leetcode347前K个高频元素
给定一个非空的整数数组,返回其中出现频率前 k 高的元素。
例如,
给定数组 [1,1,1,2,2,3] , 和 k = 2,返回 [1,2]。
注意:
- 你可以假设给定的 k 总是合理的,1 ≤ k ≤ 数组中不相同的元素的个数。
- 你的算法的时间复杂度必须优于 O(n log n) , n 是数组的大小。
提前理解:Lambda(拉姆达)表达式的语法:
基本语法:
(parameters) -> expression
或
(parameters) ->{ statements; }// 1. 不需要参数,返回值为 5 () -> 5 // 2. 接收一个参数(数字类型),返回其2倍的值 x -> 2 * x // 3. 接受2个参数(数字),并返回他们的差值 (x, y) -> x – y
解题思路:记录元素出现的频次,使用TreeMap
首先,用TreeMap
其次,遍历TreeMap中的key键值,如果优先队列没有满,则将这个元素添加到优先队列里面去,如果满了,就判断该元素出现的频次是否比队首频次最低的相比,如果大,则移除队首元素,要这个元素入队(在队尾,会根据频次来实现上浮)。
然后,因为优先队列是基于最小对实现的(最小值在队首),可以利用元素出现的频次来做优先级,频次越小的就放到队首,相对它的优先级就高。
最后,将得到的结果放到ArrayList中返回
import java.util.*;
import java.util.PriorityQueue;
/**
* leetcode Leetcode347前K个高频元素
* java默认的PriorityQueue优先队列是基于最小堆实现的,默认最小元素在队首
* 自定义优先级的话,优先级最高的再队首
*/
public class Solution2 {
//先把数组中的元素存到map中,并记录它的频次
public List topKFrequent(int[] nums, int k) {
//使用map来记录元素出现的频次
TreeMap map = new TreeMap<>();
for (int num : nums) {
if (map.containsKey(num))//如果包含则索引加1
map.put(num, map.get(num) + 1);
else
map.put(num, 1);//如果不存在这个元素,添加到map中
}
// 自定义优先级(利用最小堆的性质;最小值靠前,所以满足a-b为负数时,说明a元素该上浮)
//用拉姆达表达式替换Comparator比较器来自定义优先级
PriorityQueue pq = new PriorityQueue<>(
//拉姆达表达式返回map.get(a) - map.get(b)的值
(a, b) -> map.get(a) - map.get(b));//通过判断频次的大小实现优先级
for (int key : map.keySet()) {//对map中所有键的集合进行遍历
if (pq.size() < k)//如果优先队列中存放的数还没达到k
pq.add(key);//将这个入队,在添加元素的同时比较它的优先级
else if (map.get(key) > map.get(pq.peek())) { //如果当前元素出现的频次大于优先队列最小出现的频次(队首是最小频次)
//优先级最高(最小堆中实现的优先队列越小的值优先级应该越高)的放在队首,让这个元素出队
pq.remove();//移除队首元素(末尾的元素放到上面,siftDown()直到合适的位置)
pq.add(key);//在队尾添加元素(自动放到合适的位置实现最小堆原则)
}
}
// //输出结果,放到一个链表中
LinkedList res = new LinkedList<>();
while (!pq.isEmpty()) {//如果优先队列不为空
res.add(pq.remove());//让它的元素一个一个从队首出队进入res
}
return res;
} 测试用例:
public static void main(String[] args) {
int[] nums = {1, 1, 1, 2, 2, 3, 3, 3, 3};
int k = 3;
System.out.println((new Solution2()).topKFrequent(nums, k));
}结果:2的元素频次最少在队首
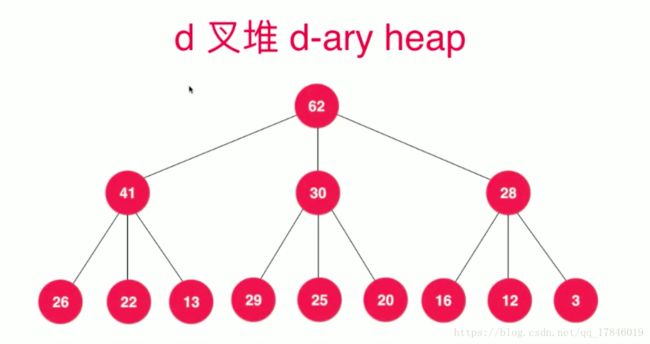
[2, 1, 3]九、和堆相关的更多话题和广义队列
d叉堆:有d个孩子的堆,也满足完全二叉树