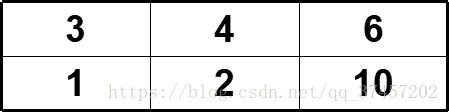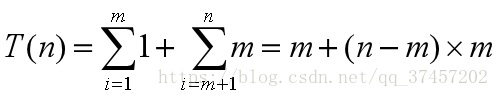算法复习笔记(六)贪心算法
序言: 学完动态规划后学习贪心算法,我们会有所感觉动态(dp)有时真的不是初学的同学能相出状态转移方程的,有些问题我们习惯上用贪心算法去解决
概述:
注意:贪心法并不是从整体最优考虑,它所做出的选择只是在某种意义上的局部最优。
这种局部最优选择并不总能获得整体最优解但通常能获得近似最优解。对于一个具体的贪心问题,怎么知道是否可以达到最优解,这个问题非常难于回答。
引入实例一:在付款问题每一步的选择中,在不超过应付款金额的条件下,只选择面值最大的货币,而不去考虑在后面看来这种选择是否合理,而且它还不会改变决定:一旦选出了一张货币,就永远选定。
方式:
先排序将最大的放在前面。
在满足条件的情况从最大的开始选
贪心法与动态规划法的区别:
动态规划法通常以自底向上(反人类操作)的方式求解各个子问题,而贪心法则通常以自顶向下的方式做出一系列的贪心选择。
贪心法的缺陷:
实例二:
钱币兑换问题2:
将n分钱兑换成1分、3分和4分的硬币,求最少需要多少枚硬币?
分析:钱币兑换问题2不具有最优子结构性质,不可以使用贪心法来求解。例如:兑换6分钱的最少只需要2枚硬币(2个3分的硬币,而不是先用4分的硬币)
实例三:
方格取数问题。
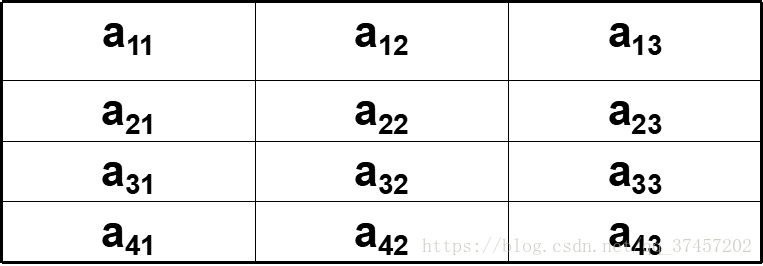
在一个N×M的方格阵中,每一格子赋予一个数,规定每次移动时只能向上或向右。找出一条路径,使其从左下角至右上角所经过的权之和最大。
分析:例如下面的一个2×3的方格阵中,每一格子都填写了一个数,求从1出发到达6,经过的数的最大和
若按贪心法求解,路径为:1→3→4→6;
若按动态规划法求解,路径为:1→2→10→6
由于贪心策略自身的特点,使得数字10所在的格子成为一个“坏格子”,即运用贪心策略找不到它,运用贪心策略求解的第一步(1→3)保证了局部最优解,却无法保证全局最优解。故本问题不能使用贪心法来求解。
贪心的关键是选择策略
组合问题中的贪心算法
实例四
背包问题
问题描述:给定n种物品和一个容量为C的背包,物品i的重量是wi,其价值为vi,背包问题是如何选择装入背包的物品,使得装入背包中物品的总价值最大?
注意与0-1背包问题的区别:再背包问题中,可以将某种物品的一部分装入背包,但不能重新装入。
分析:
选择单位重量价值最大的物品,在背包价值增长和背包容量消耗两者之间寻找平衡。
//背包问题的贪心算法实现:
#include
using namespace std;
int w[10]={20,30,10},v[10]={60,120,50}, C=50;
int Knapsack(int w[],int v[],int n)
{ int maxvalue=0,i;
for (i=0; w[i] 实例五:
活动安排问题
若区间[si, fi)与区间[sj, fj)不相交,则称活动i与活动j是相容的。
活动安排问题要求在所给的活动集合中选出最大的相容活动子集。
贪心策略:为了能安排尽量多的活动,选择结束时间最早的活动,这样可以使下一个活动尽早开始。
例如,设有11个活动等待安排,这些活动按结束时间的非递减序排列如下: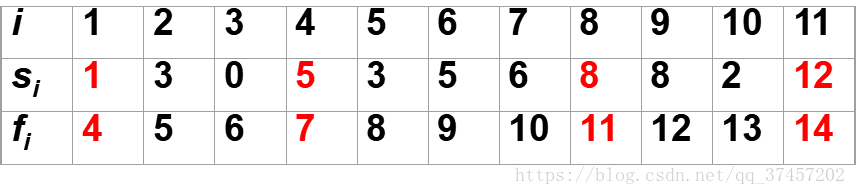
算法的时间
主要消耗在将各个活动按结束时间从小到大排序上,时间复杂性为O(nlog2n) ,而在寻找相容活动上的时间复杂性为O(n ) 。因此,算法的时间复杂性为O(nlog2n)。
//活动安排问题的贪心算法实现:
#include
using namespace std;
int s[11]={1,3,0,5,3,5,6,8,8,2,12}, f[11]={4,5,6,7,8,9,10,11,12,13,14};
int ActiveManage(int s[ ], int f[ ], int n)
{ int i,j=0,count=1;
for (i=1; i<=n; i++)
if (s[i]>=f[j]) { j=i; count++; }
return count;
}
void sort1(int s[],int f[],int n)
{ for ( int i=0;if[j+1])
{ int t=s[j];s[j]=s[j+1];s[j+1]=t;
t=f[j];f[j]=f[j+1];f[j+1]=t;
}
}
int main( )
{ sort1(s,f,11); cout< 实例六:
多机调度问题
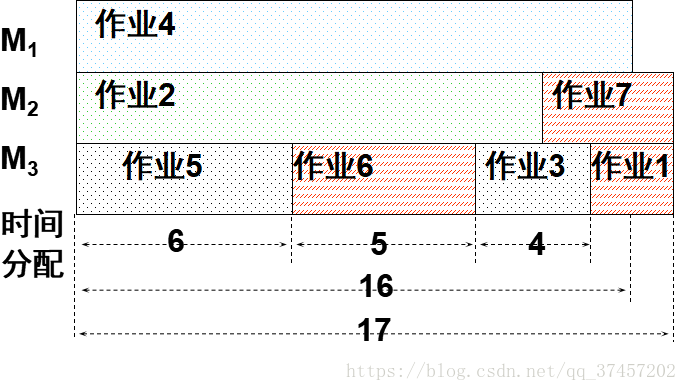
问题描述:设有n个独立的作业{1, 2, …, n},由m台相同的机器{M1, M2, …, Mm}进行加工处理,作业i所需的处理时间为ti(1≤i≤n),每个作业均可在任何一台机器上加工处理,但不可间断、拆分。多机调度问题要求给出一种作业调度方案,使所给的n个作业在尽可能短的时间内由m台机器加工处理完成。
例如:设7个独立作业{1, 2, 3, 4, 5, 6, 7}由3台机器{M1, M2, M3}加工处理,各作业所需的处理时间分别为{2, 14, 4, 16, 6, 5, 3}。
多机调度问题的贪心策略:
(1)将最长处理时间作业优先处理,
(2)当m≥n时,只要将机器i的[0, ti)时间区间分配给作业i即可;
(3)当m<n时,先将n个作业依其所需的处理时间从大到小排序,然后依此顺序将作业分配给空闲的处理机。
例如:设7个独立作业{1, 2, 3, 4, 5, 6, 7}由3台机器{M1, M2, M3}加工处理,各作业所需的处理时间分别为{2, 14, 4, 16, 6, 5, 3}。
算法描述:
1.作业时间数组t从大到小排序,数组p存放对应的作业序号;
2.将存放机器处理时间的数组d[m]初始化为0;
3.for (i=1; i<=m; i++)
3.1 S[i]=p[i]; //将作业i分配给机器i
3.2 d[i]=t[i]; //将第i个作业分配给第i台机器
4. for (i=m+1; i<=n; i++) //处理剩余的任务
4.1 寻找最先空闲的机器j;
4.2 S[j]=S[j]+{p[i]}; //将作业i分配给机器j
4.3 d[j]=d[j]+t[i]; //机器j将在d[j]后空闲
算法分析:如果采用蛮力法查找最先空闲的机器,则算法的时间复杂性为:
通常情况下m<