城市路径问题—广度优先搜算(BFS)

例题：
已知若干个城市的地图，求从一个城市到另一个城市的路径，要求该路径经过的城市最少。
城市路线图如下：

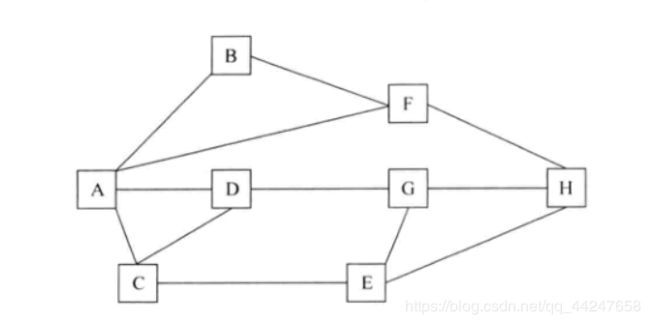
算法分析：
图的广度优先搜索类似于树的层次遍历，逐层搜索正好可以尽快找到一个结点与另一个结点相对与而言最直接的路径。所以此问题适应广度优先搜索。下面通过分许一个例子来进行算法设计：
（1）设置邻接矩阵以“1”可以走，“0”不能走。
（2）设置邻接矩阵：

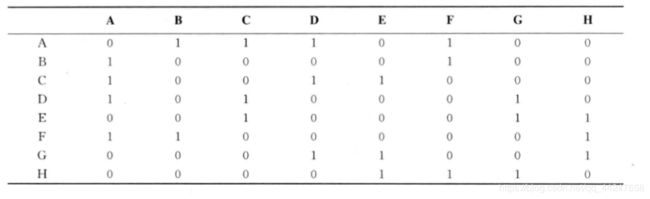
（3）
①将城市A(编号1)人队，队首指针qh置为0，队尾指针qe置为1。
②将队首指针所指城市的所有可直通的城市人队，当然如果这个城市在队中出现过就不人队，然后将队首指针加1,得到新的队首城市。重复以上步骤，直到城市H(编号为8)入队为止。当搜索到城市H时,搜索结束。
③输出经过最少城市线路。

数据结构设计:
考虑到算法的可读性,用线性数组a作为活结点队的存储空间。为了方便输出路径，队列的每个结点有两个成员,sq[i].city记录人队的城市,sq[i].pre记录该城市的前趋城市在队列中的下标，这样通过sq[i].pre就可以倒推出最短线路。也就是说活结点队同时又是记录所求路径的空间。因此，数组队并不能做成循环队列,所谓“出队”只是队首指针向后移动,其空间中存储的内容并不能被覆盖。同时和广度优先算法框架一样,设置数组visited[]记录已搜索过的城市。

---

代码如下：

#include

int jz[9][9]= {{0,0,0,0,0,0,0,0,0},{0,0,1,1,1,0,1,0,0},{0,1,0,0,0,0,1,0,0},
               {0,1,0,0,1,1,0,0,0},{0,1,0,1,0,0,0,1,0},{0,0,0,1,0,0,0,1,1},
               {0,1,1,0,0,0,0,0,1},{0,0,0,0,1,1,0,0,1},{0,0,0,0,0,1,1,1,0}};
          //1可以走，0不能走
          //因为代码中是从一开始的来方便城市的辨别，
          所以我们需要在下标为0的地方也要创建为0（即不可到达）的线路

struct sq
{
    int city;
    int pre;
} sq[100];

int qh,qe,i,visited[100];
int n=8;

void out()        //输出路径/
{
    printf("可以走的路程的路径为(数字代表城市的编号): \n\n");
    printf("%d ",sq[qe].city);
    while(sq[qe].pre!=0)
    {
        qe=sq[qe].pre;
        printf("-- %d ",sq[qe].city);
    }
    printf("\n\n");
}

void search()
{
    qh=0;
    qe=1;
    sq[1].city=1;
    sq[1].pre=0;
    visited[1]=1;
    while(qh!=qe)//当队不空//　　
    {
        qh++;                         //结点出队/
        for(i=1; i<=n; i++) //扩展结点/
            if(jz[sq[qh].city][i] == 1 && visited[i]==0)
            {
                qe++;                    //结点入队/
                sq[qe].city=i;
                sq[qe].pre=qh;
                visited[i]=1;
                if (sq[qe].city == 8)
                {
                    out();
                    return;
                }
            }
    }
    printf("没有可以走的路！/n");
}

int main()
{
    int i;
    for(i=1; i<=n; i++) //初始化visit[]
    {
        visited[i]=0;
    }
    search();
    return 0;
}

---

总结：
①图的存储空间和搜索时需要用到“队列”的存储空间
②该题目要求的是城市A-城市H的最短路径，但输出的从城市H-到城市A的最短路径。大家可以进行改进使它正序输出。
③该文中的代码引用了 “吕国英”的 《算法设计与分析》 清华大学出版社中的代码。之后会发出我已改进的城市路径问题的代码，大家可以一起探讨。