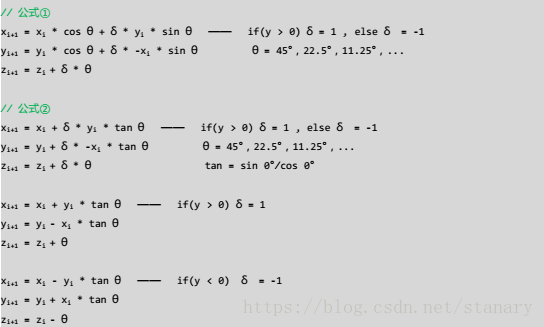CORDIC算法细则
学习更多相关知识，关注博主知乎账号，用户名Trustintruth https://www.zhihu.com/people/suo-yi-xin-90/activities
算是回来补坑吧，之前的博客中使用到了CORDIC算法的应用，但是没有详细的讲，今天我们回来抛去其他的实现，再讲一讲CORDIC算法。
之前的CORDIC文章https://blog.csdn.net/stanary/article/details/79163189
CORDIC算法
----------ch1--------------------------------------------------------------
CORDIC算法是一种全能型的数学工具，因为他有能力成为其他数学函数的替代品。
CORDIC的英文全称为Coordinate Rotation Digital Comuper，其大意为不断地旋转坐标接近答案。其真正能够一直发光发热的原因是其成本是硬件可以承担的程度。
CORDIC算法有三种功能所以可以实现不少数学函数，简单的如加减乘除，典型的的是三角函数，帅气一点的就是双曲函数。CORDIC算法自定义性很强，我们完全可以按照自己的意思去调配他。
描述语言缺乏数学的天赋...也不支持浮点数....定点数的小数点被锁死，浮点数的小数点则可以跑来跑去浮点数具有更大的计数范围，定点数的优点就是重量轻，速度快...
矢量沿着圆形的轨迹进行移动。这种情况我们叫做旋转。伪旋转：
矢量每旋转一次角度就减少一些。旋转角度被视为移动距离，源矢量每一次向目标矢量逼近，下一次的距离是上一次的一半。源矢量每次向目标矢量逼近，它的长度会越来越接近目标矢量
（一）.矢量移动的距离（角度）
（二）.矢量移动的次数（精度）
（三）.矢量移动的规则（公式）
（四）.矢量移动的方向（加减）
（五）.矢量最终的长度（结果）
CORDIC算法是一种统称，规则和模式可以千变万化，但原理都离不开以上5个核心。理论上，矢量只要拥有足够的移动次数，他就会越来越接近目标，而且距离也会越来越短。矢量一旦停止移动，他的最终长度就代表最终结果，如果移动次数足够，那么结果的精度也就会越高。源矢量会移动多少次才停止，这有两个控制选项
（一）.矢量达到预设的移动次数。
（二）.源矢量与目标矢量的距离。
一般上，移动次数可以人为，所以CORDIC算法可以随意控制他的精度与速度。换句话，要精度就拉长移动速度，要速度则缩短移动次数。CORDIC算法在执行中有一个参数会扑向（塞塔）值，这个值表示源矢量与目标矢量之间的距离，他越接近零值结果越是成熟。
CORDIC 算法除了五个核心之外，还有两个模式：
（一）.矢量模式
（二）.旋转模式
CORDIC算法在旋转模式下，矢量的旋转方向由角度决定，相对矢量模式，矢量的旋转方向则由坐标决定。
CORDIC算法还有三种功能/系统：
（一）线性函数。（加，减，乘，除）
（二）三角函数。（三角函数，反三角函数）
（三）双曲函数。 （双曲函数，反双曲函数，自然字数（e的x次方），自然对数 In x ，平方根）
对于定点数和浮点数来说，浮点数很慢，操作很麻烦，用硬件实现并不划算，而且可能坑死一堆低端设备。舍弃他是环境所迫。定点数是在IEEE上不被承认的数据类型。
一般情况下，3位十进制的小数点，或16位的二进制的小数就做够日常需求，若基于图像处理，比起精度，运算速度才重要。。
-------ch2--------------------------------------
公式一是CORDIC算法最原始的公式，其中x’表示下一个x坐标，y’表示下一个y坐标，塞塔表示旋转角度，上限是90度。
认为i是当前矢量，i+1为下一个矢量，其中x[ i ] * cos[ i ] 表示当前的 x 坐标乘上当前的cos常量，然后y*cos[ i ]表示当前的y坐标乘上当前的sin常量，两者相加成为下一个x坐标。而这些常量的来源是，角度可以看做距离，其中角度的上限是90度，矢量下一次的移动距离是上一次的一半。就结果而言，矢量每次旋转多少度，移动多少距离几乎可以预测，而且我们也可以事先建立相关的常量表。如设置16次的移动上限，所以常量表只有16位成员。
CORDIC算法有两种模式，即旋转模式和矢量模式，每一种模式都有自己的参考系。这个参考系不仅决定矢量的旋转方向，而且也间接影响坐标的加减关系。
原始公式之所以很难适用硬件实现，浮点数是原因之一，而且乘法过多也是问题。
当结尾每包含3位小数点，移动次数就要翻倍
-----------ch3------------------------------------------------
原始的公式一包含cos和sin两种函数，一旦tan函数带入进去将减少一半的的负担
矢量每次移动的距离都是上一次的一半，角度上限为90度，但矢量从45度开始向下减。
然而，公式二还是不适合硬件，所以他还要继续简化下去。问题依然是浮点数和乘法操作。
---------ch4----------------------------------------------------
继续简化
公式三在公式二的基础上，将tan函数反转再反转，结果成了更精简的公式。他和前边的家伙并没有什么两样，但他更直观，更适合硬件实现。这就是CORDIC算法的最终形态