利用python建立汽车销售厂商偷漏税用户识别模型
课题来源
“炼数成金网”《Python数据分析案例实战(第九期)》第一周作业:数据集中提供了汽车销售行业纳税人的各个属性与是否偷漏税标识。请结合汽车销售行业纳税人的各个属性,总结衡量纳税人的经营特征,建立偷漏税行为识别模型,识别偷漏税纳税人。
一、数据初步探索分析
(一)导入数据
首先,设置工作路径:
import os
os.chdir(r'E:\炼数成金:Python数据分析案例实战(第九期)\第1周')
print(os.getcwd()) # 打印当前工作目录然后,导入需要用到的python模块
import csv
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
get_ipython().magic(u'matplotlib inline') #在jupyter Notebook页面中画图
plt.rcParams['font.sans-serif'] = ['SimHei'] #此两行解决图表轴标签中文乱码问题
plt.rcParams['axes.unicode_minus']=False
df = pd.read_excel('作业1.xls')(二)初步探索
查看数据概况:
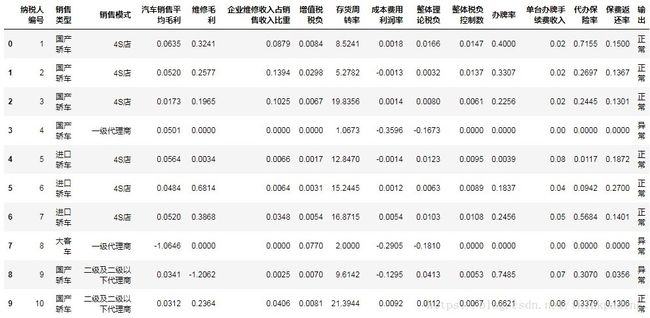
data.head(10)df.info()可见,数据包含124个样本、16个变量,没有缺失值。16个变量中,除一个纳税人编号、一个偷漏税标识外,其他14个变量都是与偷漏税有关的经营指标。进一步观察,这14个变量按类型可分为分类变量、数值变量两类,下面将从这两个方面进行探索性分析。
1、分类变量:观察偷漏税情况下的销售类型和销售模式分布
销售的汽车类型和销售模式可能会对偷漏税倾向有一定的表征,因此,画出“输出结果为异常的销售类型和销售模式”的分布图可能可以直观上看出是否有一定影响。
fig=plt.figure()
fig.set(alpha=0.2)
plt.subplot2grid((1,2),(0,0))
df_type=df[u'销售类型'][df[u'输出']=='异常'].value_counts()
df_type.plot(kind='bar',color='blue')
plt.title(u'不同销售类型下的偷漏税情况',fontproperties='SimHei')
plt.xlabel(u'销售类型',fontproperties='SimHei')
plt.ylabel(u'异常数',fontproperties='SimHei')
plt.subplot2grid((1,2),(0,1))
df_model=df[u'销售模式'][df[u'输出']=='异常'].value_counts()
df_model.plot(kind='bar',color='green')
plt.title(u'不同销售模式下的偷漏税情况',fontproperties='SimHei')
plt.xlabel(u'销售模式',fontproperties='SimHei')
plt.ylabel(u'异常数',fontproperties='SimHei')
plt.subplots_adjust(wspace=0.3)
plt.show()运行结果如下图:

分析:从图中可以看出,对于存在偷漏税行为的纳税人中,销售国产轿车的最多,通过4S店模式销售的最多。但这只是一个分布情况,具体有无关系尚不确定。
2、数值变量:观察偷漏税情况下的其他变量分布
原始数据中根本无法看出任何规律,因此,这里对正常、异常两种情况下的数据进行探索:
#分别输出正常、异常情况下的数值型变量的分布情况
df_normal=df.iloc[:,3:15][df['输出']=='正常'].describe().T
df_normal=df_normal[['count','mean','max','min','std']]
df_abnormal=df.iloc[:,3:15][df['输出']=='异常'].describe().T
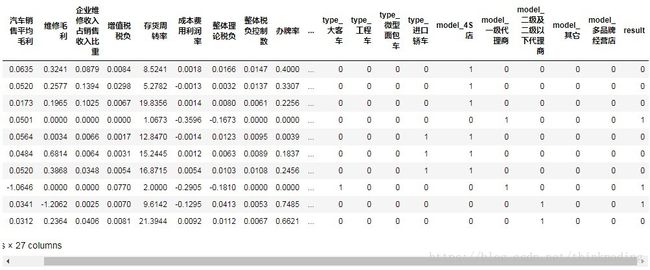
df_abnormal=df_abnormal[['count','mean','max','min','std']]运行结果得到正常、异常情况下的数据概况:

观察:从平均值可以看到,在正常、异常情况下,汽车销售平均毛利、维修毛利、整体税负控制数这三个变量还是存在明显差异的,但这只是一个观察结果,只能作为一种猜想来考虑。
二、数据预处理
数据预处理主要包括缺失值、异常值处理、数值转换等。本文数据样本无缺失值,因此不需要进行缺失值处理。由于笔者对汽车销售行业相关经营指标的不熟悉,无法判断有无异常值,因此暂时也不进行异常值处理。
但是涉及到分类变量,在模型建立时,需将分类变量转换成虚拟变量,因此,博主在数据预处理的过程中,主要对销售类型、销售模式以及输出进行虚拟变量的建立。
Pandas中有直接转换的函数,get_dummies,参数prefix为转换后列名的前缀。
虚拟变量建立代码如下:
#数据预处理(将销售类型与销售模式以及输出转换成虚拟变量)
type_dummies=pd.get_dummies(df[u'销售类型'],prefix='type')
model_dummies=pd.get_dummies(df[u'销售模式'],prefix='model')
result_dummies=pd.get_dummies(df[u'输出'],prefix='result')
df=pd.concat([df,type_dummies,model_dummies,result_dummies],axis=1)
#去除被替代的列
df.drop([u'销售类型',u'销售模式',u'输出'],axis=1,inplace=True)
#正常列去除,异常列作为结果
df.drop([u'result_正常'],axis=1,inplace=True)
df.rename(columns={u'result_异常':'result'},inplace=True)三、模型选择与建立
目前,笔者正在学习CART决策树模型和逻辑回归模型,因此,本课题就采用这两种模型来建立。
首先,需要将数据集划分为训练集、测试集,按照常用方法,本文依旧选取80%为训练集,20%为测试集。代码如下:
data = df.as_matrix() #将表格转换为矩阵
from random import shuffle #导入随机函数shuffle,用来打乱数据
shuffle(data) #随机打乱数据
#数据划分(80%作为训练数据,20%作为测试数据)
p=0.8
data_train=data[:int(len(data)*p)]
data_test=data[int(len(data)*p):]接下来,分别建立CART决策树模型和逻辑回归模型。
(一)CART决策树模型
首先,导入决策树模块,并进行训练:
#构建CART决策树模型
from sklearn.tree import DecisionTreeClassifier #导入决策树模型
y=data_train[:,-1]
x=data_train[:,1:-1]
tree = DecisionTreeClassifier() #建立决策树模型
tree.fit(x, y) #训练保存模型:
#保存模型
from sklearn.externals import joblib
joblib.dump(tree, r'E:\炼数成金:Python数据分析案例实战(第九期)\第1周\homework\thoughts_tree.pkl')接下来,为分析模型的分类效果,计划采用“显示混淆矩阵可视化结果”的方法来观察,为此,首先需要创建一个方法:
###构建模型####
def cm_plot(y, yp):
from sklearn.metrics import confusion_matrix
cm = confusion_matrix(y, yp)
import matplotlib.pyplot as plt
plt.matshow(cm, cmap=plt.cm.Greens)
plt.colorbar()
for x in range(len(cm)):
for y in range(len(cm)):
plt.annotate(cm[x,y], xy=(x, y), horizontalalignment='center', verticalalignment='center')
plt.ylabel('True label')
plt.xlabel('Predicted label')
return plt然后,调用该方法显示混淆矩阵可视化结果:
cm_plot(y, tree.predict(x)).show() #显示混淆矩阵可视化结果
#注意到Scikit-Learn使用predict方法直接给出预测结果。
cm_plot(data_test[:,-1],tree.predict(data_test[:,1:-1])).show()运行结果如下:
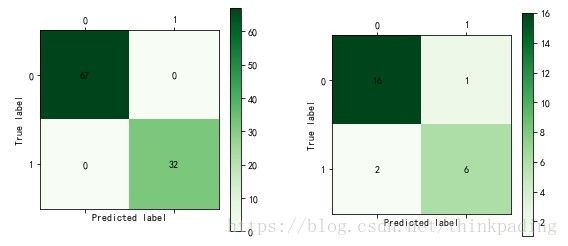
分析:从上图可以看出,对于训练集来说,决策树模型的准确率为100%;对于测试集来说,其准确率为22/25=88%,正常纳税人中,被判定为偷漏税用户的比例为1/17=5.9%,异常纳税人中,被判定为正常用户的比例为2/8=25%。
注:每次重新计算的时候,测试集的混淆矩阵可视化结果可能不同。
(二)逻辑回归模型
利用Python建立逻辑回归模型,可以从sklearn包中导入线性模型linear_model,就可以直接对逻辑回归模型进行调用,模型建立之后同样分别绘制训练样本和测试样本的混淆矩阵,并且输出逻辑回归的系数。
代码如下:
#逻辑回归
from sklearn import linear_model
clf=linear_model.LogisticRegression(C=1.0,penalty='l1',tol=1e-6)
#此处的x,y与上文中决策树所用x,y相同
clf.fit(x,y)
#逻辑回归系数
xishu=pd.DataFrame({"columns":list(df.columns)[1:-1], "coef":list(clf.coef_.T)})
#逻辑回归混淆矩阵
cm_plot(y,clf.predict(x)).show()
#对test数据进行预测
predictions=clf.predict(data_test[:,1:-1])
cm_plot(data_test[:,-1],predictions).show()运行结果如下图所示:
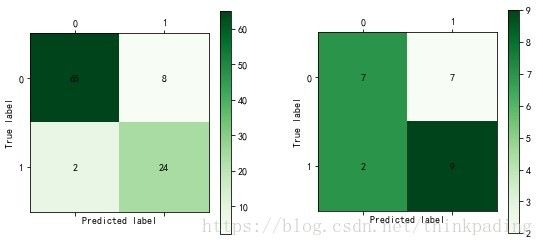
分析:从上图可以看出,对于训练集来说,逻辑回归模型的准确率为(65+24)/99=89.9%,正常纳税人中,被判定为偷漏税用户的比例为8/73=11%,异常纳税人中,被判定为正常用户的比例为2/26=7.69%;对于测试集来说,其准确率为(7+9)/25=64%,正常纳税人中,被判定为偷漏税用户的比例为7/14=50%,异常纳税人中,被判定为正常用户的比例为2/11=18.18%。
逻辑回归系数为:
xishu

分析:通过系数观察出,维修毛利、代办保险率对偷漏税有明显的负相关,办牌率、一级代理商和其他销售模式对偷漏税有明显的正相关。也就是说,纳税人维修毛利越高,代办保险率越高,其偷漏税倾向将会越低;而办牌率越高,销售模式为一级代理商和其他销售模式,则该纳税人将更有可能为偷漏税用户。
四、模型比较
根据第三部分的混淆矩阵可视化结果、分类准确率来看,无论对于训练集还是测试集,CART决策树模型都要比逻辑回归模型的分类效果好一些。为进一步比较两个模型的性能,绘制出两个模型的ROC曲线。
#两个分类方法的ROC曲线
from sklearn.metrics import roc_curve #导入ROC曲线函数
import matplotlib.pyplot as plt
fig,ax=plt.subplots()
fpr, tpr, thresholds = roc_curve(data_test[:,-1], tree.predict_proba(data_test[:,1:-1])[:,1], pos_label=1)
fpr2, tpr2, thresholds2 = roc_curve(data_test[:,-1], clf.predict_proba(data_test[:,1:-1])[:,1], pos_label=1)
plt.plot(fpr, tpr, linewidth=2, label = 'ROC of CART', color = 'blue') #作出ROC曲线
plt.plot(fpr2, tpr2, linewidth=2, label = 'ROC of LR', color = 'green') #作出ROC曲线
plt.xlabel('False Positive Rate') #坐标轴标签
plt.ylabel('True Positive Rate') #坐标轴标签
plt.ylim(0,1.05) #边界范围
plt.xlim(0,1.05) #边界范围
plt.legend(loc=4) #图例
plt.show() #显示作图结果运行结果如下:
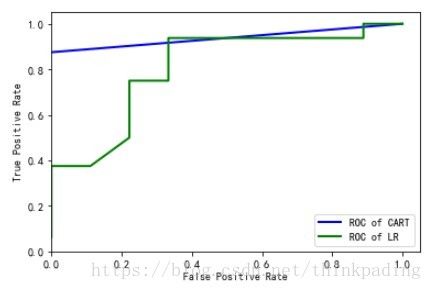
分析:ROC曲线越靠近左上角,则模型性能越优,两个曲线做于同一个坐标时,若一个模型的曲线完全包住另一个模型,则前者优,当两者有交叉时,则看曲线下的面积,上图明显蓝色线下的面积更大,即CART决策树模型性能更优。
由此可见,对于本数据集而言,CART决策树模型不管从混淆矩阵还是ROC曲线来看,其性能都要优于逻辑回归模型。
五、总结
本次研究涉及了数据分析基本流程、CART决策树模型建立、逻辑回归模型建立、混淆矩阵可视化结果、ROC曲线绘制,采用科学方法建立了数据模型并对模型进行评价。
本次研究也存在一定问题,混淆矩阵图和ROC曲线图几乎每一次运行结果都不一样,除了CART决策树模型的训练样本,也就是准确率为100%的那个图是不变的,其他的图一直都在变化,说明预测结果一直都在变化。尚不知是什么原因。
数据下载:
参考资源:《Python数据分析与挖掘实战》第六章学习拓展——偷漏税用户识别https://blog.csdn.net/sinat_33519513/article/details/74086061