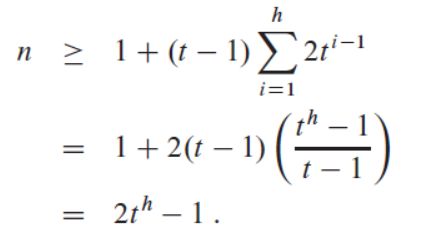一、定义
1.1 B树的概念
在一些大规模的数据存储中,如数据库,分布式系统等,数据的访问经常需要进行磁盘的读写操作,这个时候的瓶颈主要就在于磁盘的I/O上。
如果采用普通的二叉查找树结构,由于树的深度过大,会造成磁盘I/O的读写过于频繁,进而导致访问效率低下(因为一般树的一个结点对应一个磁盘的页,所以深度越大,读取磁盘页越频繁)。
那么,如何减少树的深度?
一个基本的想法就是:采用多叉树结构,在结点总数一定的情况下,结点分支越多,树的高度也就越小,从而查询的效率也就越高。从这个意义上来看,就有了B树的结构。
M阶B树定义:
B树常用“阶”来定义,一棵M阶B树,要么是一棵空树或者只有一个根结点,要么具有如下性质:
- 根结点的子结点数在[2,M]之间;
- 除根结点外,所有非叶子结点的子结点数范围:
3、所有叶子结点的高度都相同。
B树的检索过程:
- 在当前结点中对关键码进行二分法检索:
①如果找到检索关键码,就返回这条记录
②如果当前结点是叶子结点且未找到关键码,则返回检索失败 - 否则,沿着正确的分支重复这一过程。
1.2 B+树的概念
B树广泛用于实现基于磁盘的大型系统中。实际上,B树几乎从来没有被实现过,工业上最常使用的是B树的一个变种——B+树。
B+树与B树的最大区别在于:
- B+树只在叶子结点中存储记录(或存储指向记录的指针),而内部结点仅存储关键码(这些关键码仅仅用于引导检索);
- B+树的叶结点一般链接起来,形成一个双向链表。
二、实现
本文中的实现是B树的一种变种,类似B+树,主要是为了说明B树这一数据结构。
2.1 数据结构定义
树结点定义:
树结点分为两类:
- 内部结点
仅存储关键码值(在以内部结点为根的子树中,所有的键都大于等于与此内部结点关联的键,但小于此内部结点中次大的键) - 外部结点
即叶子结点,存储记录(或存储指向记录的指针)
注意:上图中定义了一个哨兵键 " * ",哨兵键小于任何键(根结点的第一个键是哨兵键,哨兵键所指向结点的第一个键也是哨兵键)
源码:
// 结点定义
private static final class Node {
private int m; // 实际子结点数:m ≤ M
private boolean isLeaf;
// M阶B树的每个结点含有M个指向子结点的指针(其中内部结点的children[0]表示哨兵,小于任何键)
private Entry[] children = new Entry[M];
private Node(int k,boolean isLeaf) {
m = k;
this.isLeaf = isLeaf;
}
}
private static class Entry {
private Comparable key; // 键码值
private final Object val; // 实际的记录值(或指向记录的)
private Node next;
public Entry(Comparable key, Object val, Node next) {
this.key = key;
this.val = val;
this.next = next;
}
}
2.2 基本操作的实现
2.2.1 查找
查找时,从根结点开始,根据被查找的键选择当前结点中的适当区间,并根据适当的链接从一个结点移动到下一个结点。
最终,查找过程会到达叶子结点。如果被查找的键在叶子结点中,则命中,否则未命中。
查找源码:
public Value get(Key key) {
if (key == null)
throw new IllegalArgumentException("argument to get() is null");
return search(root, key);
}
//在以x为根结点的树中查找键值key
private Value search(Node x, Key key) {
Entry[] children = x.children;
if (x.isLeaf) { // 外部结点,直接判断是否和被查找键相等
for (int j = 0; j < x.m; j++) {
if (eq(key, children[j].key))
return (Value) children[j].val;
}
} else { // 内部结点
for (int j = 0; j < x.m; j++) { // children[0]可能表示哨兵
if (j + 1 == x.m || less(key, children[j + 1].key))
return search(children[j].next, key);
}
}
return null;
}
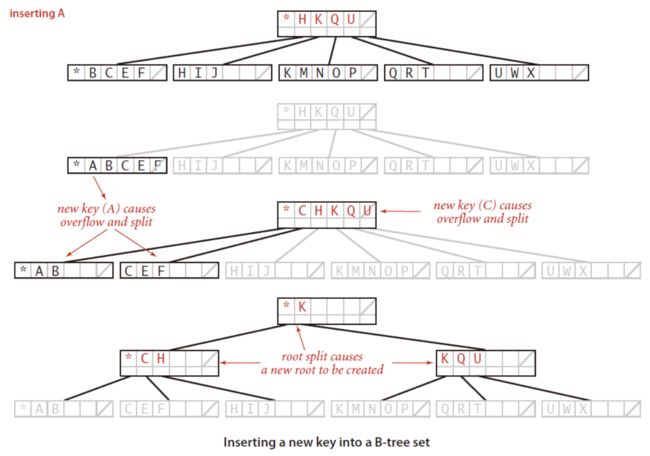
2.2.2 插入
B树的插入过程与查找类似。
首先进行查找,找到待插入的叶子结点:
①如果叶子结点还没有满(一般“满”是指插入后子结点数量超过M,但实际应用中一般会定义一个百分比,元素占比超过该百分比则认为溢出),那么直接插入;
②如果叶子结点已经满了,就把它分裂成两个结点(平均分配),然后将新形成的右边结点的最小键码值复制一份到父结点。如果父结点也满了,则执行相同操作,直到到达根结点或引起根结点分裂(树高增加1).
插入源码:
public void put(Key key, Value val) {
if (key == null)
throw new IllegalArgumentException("argument key to put() is null");
Node u = insert(root, key, val);
n++;
if (u == null)
return;
// 说明根结点需要分裂
Node t = new Node(2);
t.children[0] = new Entry(root.children[0].key, null, root); //复用root
t.children[1] = new Entry(u.children[0].key, null, u);
root = t;
height++;
}
/**
* 在以x为根的B树中插入键值对
* @return 若插入结点后未满(子结点数小于M),则返回null;否则,分裂结点,返回分裂后新的右边结点
*/
private Node insert(Node x, Key key, Value val) {
int j;
Entry t = new Entry(key, val, null);
if (x.isLeaf) { // 叶子结点,找到第一个比key大的位置j
for (j = 0; j < x.m; j++) {
if (less(key, x.children[j].key))
break;
}
} else { // 内部结点,找到key所属的位置j
for (j = 0; j < x.m; j++) {
if ((j + 1 == x.m) || less(key, x.children[j + 1].key)) {
Node u = insert(x.children[j].next, key, val);
if (u == null)
return null;
t.key = u.children[0].key;
t.next = u;
break;
}
}
}
//右移元素,给待插入键留出空位
for (int i = x.m; i > j; i--)
x.children[i] = x.children[i - 1];
x.children[j] = t;
x.m++;
if (x.m < M)
return null;
else
return split(x);
}
//分裂结点,返回分裂后的右边结点
private Node split(Node h) {
Node t = new Node(M / 2);
h.m = M / 2;
for (int j = 0; j < M / 2; j++)
t.children[j] = h.children[M / 2 + j];
return t;
}
2.3 完整源码
public class BTree, Value> {
// max children per B-tree node = M-1
// (must be even and greater than 2)
private static final int M = 4;
private Node root; // root of the B-tree
private int height; // height of the B-tree
private int n; // number of key-value pairs in the B-tree
// helper B-tree node data type
private static final class Node {
private int m; // number of children
private Entry[] children = new Entry[M]; // the array of children
// create a node with k children
private Node(int k) {
m = k;
}
}
// internal nodes: only use key and next
// external nodes: only use key and value
private static class Entry {
private Comparable key;
private final Object val;
private Node next; // helper field to iterate over array entries
public Entry(Comparable key, Object val, Node next) {
this.key = key;
this.val = val;
this.next = next;
}
}
/**
* Initializes an empty B-tree.
*/
public BTree() {
root = new Node(0);
}
/**
* Returns true if this symbol table is empty.
*
* @return {@code true} if this symbol table is empty; {@code false}
* otherwise
*/
public boolean isEmpty() {
return size() == 0;
}
/**
* Returns the number of key-value pairs in this symbol table.
*
* @return the number of key-value pairs in this symbol table
*/
public int size() {
return n;
}
/**
* Returns the height of this B-tree (for debugging).
*
* @return the height of this B-tree
*/
public int height() {
return height;
}
/**
* Returns the value associated with the given key.
*
* @param key
* the key
* @return the value associated with the given key if the key is in the
* symbol table and {@code null} if the key is not in the symbol
* table
* @throws IllegalArgumentException
* if {@code key} is {@code null}
*/
public Value get(Key key) {
if (key == null)
throw new IllegalArgumentException("argument to get() is null");
return search(root, key, height);
}
private Value search(Node x, Key key, int ht) {
Entry[] children = x.children;
// external node
if (ht == 0) {
for (int j = 0; j < x.m; j++) {
if (eq(key, children[j].key))
return (Value) children[j].val;
}
}
// internal node
else {
for (int j = 0; j < x.m; j++) {
if (j + 1 == x.m || less(key, children[j + 1].key))
return search(children[j].next, key, ht - 1);
}
}
return null;
}
/**
* Inserts the key-value pair into the symbol table, overwriting the old
* value with the new value if the key is already in the symbol table. If
* the value is {@code null}, this effectively deletes the key from the
* symbol table.
*
* @param key
* the key
* @param val
* the value
* @throws IllegalArgumentException
* if {@code key} is {@code null}
*/
public void put(Key key, Value val) {
if (key == null)
throw new IllegalArgumentException("argument key to put() is null");
Node u = insert(root, key, val, height);
n++;
if (u == null)
return;
// need to split root
Node t = new Node(2);
t.children[0] = new Entry(root.children[0].key, null, root);
t.children[1] = new Entry(u.children[0].key, null, u);
root = t;
height++;
}
private Node insert(Node h, Key key, Value val, int ht) {
int j;
Entry t = new Entry(key, val, null);
// external node
if (ht == 0) {
for (j = 0; j < h.m; j++) {
if (less(key, h.children[j].key))
break;
}
}
// internal node
else {
for (j = 0; j < h.m; j++) {
if ((j + 1 == h.m) || less(key, h.children[j + 1].key)) {
Node u = insert(h.children[j++].next, key, val, ht - 1);
if (u == null)
return null;
t.key = u.children[0].key;
t.next = u;
break;
}
}
}
for (int i = h.m; i > j; i--)
h.children[i] = h.children[i - 1];
h.children[j] = t;
h.m++;
if (h.m < M)
return null;
else
return split(h);
}
// split node in half
private Node split(Node h) {
Node t = new Node(M / 2);
h.m = M / 2;
for (int j = 0; j < M / 2; j++)
t.children[j] = h.children[M / 2 + j];
return t;
}
/**
* Returns a string representation of this B-tree (for debugging).
*
* @return a string representation of this B-tree.
*/
public String toString() {
return toString(root, height, "") + "\n";
}
private String toString(Node h, int ht, String indent) {
StringBuilder s = new StringBuilder();
Entry[] children = h.children;
if (ht == 0) {
for (int j = 0; j < h.m; j++) {
s.append(indent + children[j].key + " " + children[j].val + "\n");
}
} else {
for (int j = 0; j < h.m; j++) {
if (j > 0)
s.append(indent + "(" + children[j].key + ")\n");
s.append(toString(children[j].next, ht - 1, indent + " "));
}
}
return s.toString();
}
// comparison functions - make Comparable instead of Key to avoid casts
private boolean less(Comparable k1, Comparable k2) {
return k1.compareTo(k2) < 0;
}
private boolean eq(Comparable k1, Comparable k2) {
return k1.compareTo(k2) == 0;
}
/**
* Unit tests the {@code BTree} data type.
*
* @param args
* the command-line arguments
*/
public static void main(String[] args) {
BTree st = new BTree();
st.put("www.cs.princeton.edu", "128.112.136.12");
st.put("www.cs.princeton.edu", "128.112.136.11");
st.put("www.princeton.edu", "128.112.128.15");
st.put("www.yale.edu", "130.132.143.21");
st.put("www.simpsons.com", "209.052.165.60");
st.put("www.apple.com", "17.112.152.32");
st.put("www.amazon.com", "207.171.182.16");
st.put("www.ebay.com", "66.135.192.87");
st.put("www.cnn.com", "64.236.16.20");
st.put("www.google.com", "216.239.41.99");
st.put("www.nytimes.com", "199.239.136.200");
st.put("www.microsoft.com", "207.126.99.140");
st.put("www.dell.com", "143.166.224.230");
st.put("www.slashdot.org", "66.35.250.151");
st.put("www.espn.com", "199.181.135.201");
st.put("www.weather.com", "63.111.66.11");
st.put("www.yahoo.com", "216.109.118.65");
StdOut.println("cs.princeton.edu: " + st.get("www.cs.princeton.edu"));
StdOut.println("hardvardsucks.com: " + st.get("www.harvardsucks.com"));
StdOut.println("simpsons.com: " + st.get("www.simpsons.com"));
StdOut.println("apple.com: " + st.get("www.apple.com"));
StdOut.println("ebay.com: " + st.get("www.ebay.com"));
StdOut.println("dell.com: " + st.get("www.dell.com"));
StdOut.println();
StdOut.println("size: " + st.size());
StdOut.println("height: " + st.height());
StdOut.println(st);
StdOut.println();
}
}
三、性能分析
典型的B树通常只需要访问2-3次即可确定元素,而且根结点可以放在内存中进行缓存,进一步提高效率。
含有N个元素的M阶B树,其一次查找或插入需要logMN ~ log(M/2)N 次探查——实际情况下基本是一个很小的常数。
对于一颗包含N个关键字的M阶树来说,其最大高度不会超过log(M/2)(N+1)/2
上述定理证明:
要使树的高度最大,则每个结点应包含尽量少的子结点。
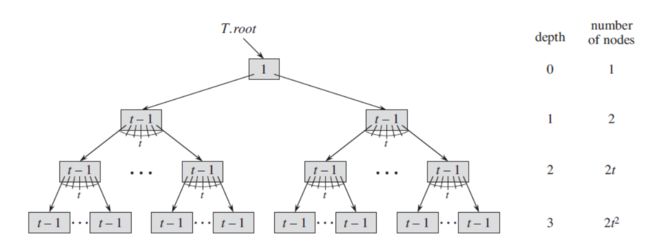
假设M阶树含有n个关键字,每个结点的最小子结点数为t(除根结点和叶子结点外,t=M/2),则树的高度为h有如下关系(从0计起):
h=0层,结点数为1
h=1层,结点数为2
h=2层,结点数为2t
h=3层,结点数为2t2
由于每个结点的最小子结点数为t,则结点的键数目为t-1(根结点为1),那么:
即h ≤ logt(n+1)/2