Apollo代码学习(五)—横纵向控制
Apollo代码学习—横纵向控制
- 前言
- 纵向控制
- 横向控制
- 前馈控制
- 注意
- 反馈控制
- 总结
- 补充 2018.11.28
前言
在我的第一篇博文:Apollo代码学习(一)—控制模块概述中,对横纵向控制做了基本概述,现在做一些详细分析。
纵向控制
纵向控制主要为速度控制,通过控制刹车、油门、档位等实现对车速的控制,对于自动挡车辆来说,控制对象其实就是刹车和油门。
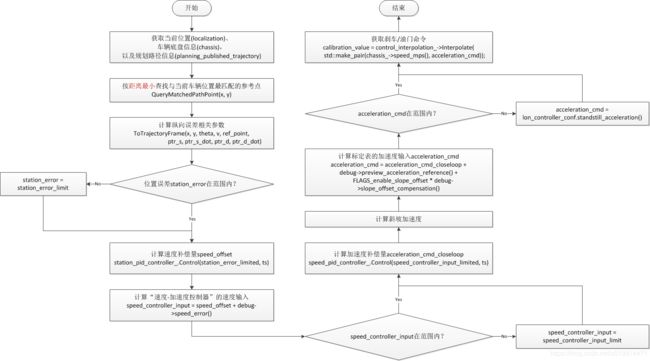
Apollo纵向控制的工作原理如图1所示。它主要由“位移-速度闭环PID控制器”、“速度-加速度闭环PID控制器”和“速度-加速度-刹车/油门”开环控制器构成。
| 位置PID闭环控制器 | 速度PID闭环控制器 | 标定表开环控制器 | |||
|---|---|---|---|---|---|
| 输入 | 期望位置+当前实际位置 | 输入 | 速度补偿+当前位置速度偏差 | 输入 | 加速度补偿+规划加速度,当前车速 |
| 输出 | 速度补偿量 | 输出 | 加速度补偿量 | 输出 | 油门/刹车控制量 |
以不加预估的控制为例,apollo纵向控制中计算纵向误差的原理:
其中,重要的是纵向误差的计算,纵向误差包含两个状态变量:
- 速度误差( s p e e d _ e r r o r speed\_error speed_error)
- 位置误差( s t a t i o n _ e r r o r station\_error station_error)
跟计算纵向误差相关的函数主要是:
void TrajectoryAnalyzer::ToTrajectoryFrame(const double x, const double y,
const double theta, const double v,
const PathPoint &ref_point,
double *ptr_s, double *ptr_s_dot,
double *ptr_d,
double *ptr_d_dot)
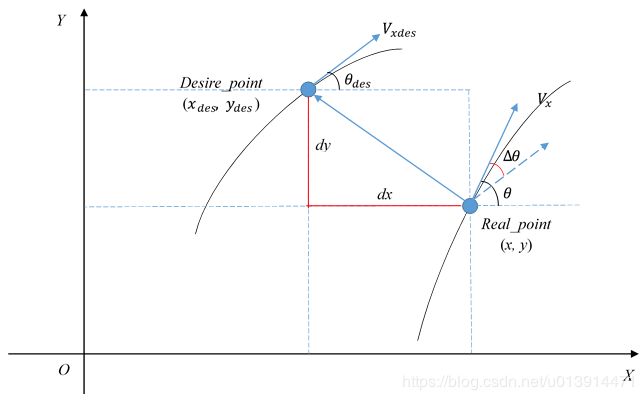
计算的原理和Apollo代码学习(三)—车辆动力学模型中的图5类似,由Optimal Trajectory Generation for Dynamic Street Scenarios in a Frenet Frame中的图3转化而来:
与图3的区别是,图4不假设由 R e a l p o i n t Real_point Realpoint指向 D e s i r e p o i n t Desire_point Desirepoint的向量和 V x V_x Vx一定垂直,因为在trajectory_analyzer.cc的注释中有:
// reference: Optimal trajectory generation for dynamic street scenarios in a
// Frenét Frame,
// Moritz Werling, Julius Ziegler, Sören Kammel and Sebastian Thrun, ICRA 2010
// similar to the method in this paper without the assumption the "normal"
// vector
// (from vehicle position to ref_point position) and reference heading are
// perpendicular.
位置误差的计算:
// trajectory_analyzer.cc
double dx = x - ref_point.x();
double dy = y - ref_point.y();
double dot_rd_nd = dx * cos_ref_theta + dy * sin_ref_theta;
*ptr_s = ref_point.s() + dot_rd_nd;
// lon_controller.cc
// s_matched即上面的ptr_s
debug->set_station_error(reference_point.path_point().s() - s_matched);
由此可知,位置误差为:
(1) s t a t i o n _ e r r o r = − ( d x ∗ cos θ d e s + d y ∗ sin θ d e s ) station\_error=-(dx*\cos{\theta_{des}} + dy*\sin{\theta_{des}}) \tag{1} station_error=−(dx∗cosθdes+dy∗sinθdes)(1)
速度误差的计算:
// trajectory_analyzer.cc
double cross_rd_nd = cos_ref_theta * dy - sin_ref_theta * dx;
*ptr_d = cross_rd_nd;
double delta_theta = theta - ref_point.theta();
double cos_delta_theta = std::cos(delta_theta);
double sin_delta_theta = std::sin(delta_theta);
double one_minus_kappa_r_d = 1 - ref_point.kappa() * (*ptr_d);
if (one_minus_kappa_r_d <= 0.0) {
AERROR << "TrajectoryAnalyzer::ToTrajectoryFrame "
"found fatal reference and actual difference. "
"Control output might be unstable:"
<< " ref_point.kappa:" << ref_point.kappa()
<< " ref_point.x:" << ref_point.x()
<< " ref_point.y:" << ref_point.y() << " car x:" << x
<< " car y:" << y << " *ptr_d:" << *ptr_d
<< " one_minus_kappa_r_d:" << one_minus_kappa_r_d;
// currently set to a small value to avoid control crash.
one_minus_kappa_r_d = 0.01;
}
*ptr_s_dot = v * cos_delta_theta / one_minus_kappa_r_d;
// lon_controller.cc
// s_dot_matched即上面的ptr_s_dot
debug->set_speed_error(reference_point.v() - s_dot_matched);
由此可知,速度误差为:
(2) s p e e d _ e r r o r = V d e s − V ∗ cos Δ θ / k speed\_error=V_{des} - V*\cos{\Delta\theta}/k \tag{2} speed_error=Vdes−V∗cosΔθ/k(2)
其中, V d e s V_{des} Vdes为期望车辆线速度, V V V为当前车辆线速度, Δ θ \Delta\theta Δθ为航向误差, k k k为系数,即代码中的 o n e _ m i n u s _ k a p p a _ r _ d one\_minus\_kappa\_r\_d one_minus_kappa_r_d 。
求得位移误差和速度误差后,结合“位移-速度闭环PID控制器”和“速度-加速度闭环PID控制器”,求得刹车/油门标定表的两个输入量:速度和加速度,利用插值计算在标定表中查找相应的控制命令值。
Apollo所用的PID控制器就是位置型PID控制器:
(3) u ( k ) = K P e ( k ) + K I ∑ i = 1 k e ( i ) + K D [ e ( k ) − e ( k − 1 ) ] u(k)=K_Pe(k)+K_I\sum_{i=1}^k e(i)+K_D[e(k)-e(k-1)] \tag{3} u(k)=KPe(k)+KIi=1∑ke(i)+KD[e(k)−e(k−1)](3)
// 微分项
diff = (error - previous_error_) / dt;
// 积分项
integral_ += error * dt * ki_;
// PID控制器输出
output = error * kp_ + integral_ + diff * kd_;
在实际调参过程中先调节P参数,再调节D参数,可能会更快达到想要的效果。感谢Apollo开发者群里哈工大的海洋同学在PID调参过程中给我的指点。
横向控制
横向控制主要控制航向,通过改变方向盘扭矩或角度的大小等,使车辆按照想要的航向行驶。Apollo中的横向控制主要由前馈开环控制器和反馈闭环控制器构成。
前馈控制
在之前的博文中提到,车辆的系统的一般状态方程为:
(4) x ˙ = A x + B u \dot{x}=Ax+Bu\tag{4} x˙=Ax+Bu(4)
其中, u u u为前轮转角 δ \delta δ,但由于道路曲率 φ ˙ d e s \dot{\varphi}_{des} φ˙des的存在,公式4应写为
(5) x ˙ = A x + B δ + B 2 φ ˙ d e s \dot{x}=Ax+B\delta+B_2\dot{\varphi}_{des} \tag{5} x˙=Ax+Bδ+B2φ˙des(5)
当车辆在曲线道路上行驶时,并不能完全消除跟踪误差,因此引入和道路曲率相关的前馈控制器以帮助消除跟踪误差,由代码可以看出:
const double steer_angle_feedforward = ComputeFeedForward(debug->curvature());
输入量只有一个曲率,计算的依据:
(6) δ f f = L R + K V a y − k 3 [ ℓ r R − ℓ f 2 C α r m V x 2 R ℓ ] \delta_{ff}=\frac{L}{R}+K_Va_y-k_3[\frac{\ell_r}{R}-\frac{\ell_f}{2C_{\alpha r}}\frac{m{V_x}^2}{R\ell}] \tag{6} δff=RL+KVay−k3[Rℓr−2CαrℓfRℓmVx2](6)
公式出处:Vehicle Dynamics and Control 第3章,该章节对方向盘控制做了详解。
公式6中 δ f f \delta_{ff} δff为前轮转角,需要乘以传动比,然后转换为方向盘转动率。
const double steer_angle_feedforwardterm =
(wheelbase_ * ref_curvature + kv * v * v * ref_curvature -
matrix_k_(0, 2) *
(lr_ * ref_curvature -
lf_ * mass_ * v * v * ref_curvature / 2 / cr_ / wheelbase_)) *
180 / M_PI * steer_transmission_ratio_ /
steer_single_direction_max_degree_ * 100;
其中, r e f _ c u r v a t u r e ref\_curvature ref_curvature 为曲率, r e f _ c u r v a t u r e = 1 R ref\_curvature = \frac{1}{R} ref_curvature=R1, k 3 = m a t r i x _ k _ ( 0 , 2 ) k_3=matrix\_k\_(0, 2) k3=matrix_k_(0,2), m a t r i x _ k _ matrix\_k\_ matrix_k_为增益矩阵,由LQR求得。
注意
有博友提示此处前馈控制的代码和公式6有出入,经比较确实有误,
参看modules\control\conf\lincoln.pb.txtapollo中的配置信息,cr_和cf_均为155494.663;
参看 Vehicle Dynamics and Control一书中3.1章节的的例子,单侧转动惯量一般为80000左右,二者为2倍的关系;
结合代码中其他用到cr_和cf_的地方,以及书中公式,可能是代码有误,这需要向开发者提交求证。
反馈控制
由于前馈控制用于消除有道路曲率引起的误差,因此对于反馈控制,车辆的状态方程仍可以用公式4表示:
(4) x ˙ = A x + B u \dot{x}=Ax+Bu\tag{4} x˙=Ax+Bu(4)
为了达到性能上的需求,并使控制系统构成全状态反馈系统,需要设计一个反馈控制器 u = − K x u=-Kx u=−Kx。基于车辆系统的状态方程,并结合代码进行分析,仍先不考虑预估,即preview_window_=0。
首先,控制系统的状态变量有四个:
- 横向误差 l a t e r a l _ e r r o r lateral\_error lateral_error
- 横向误差率 l a t e r a l _ e r r o r _ r a t e lateral\_error\_rate lateral_error_rate
- 航向误差 h e a d i n g _ e r r o r heading\_error heading_error
- 航向误差率 h e a d i n g _ e r r o r _ r a t e heading\_error\_rate heading_error_rate
横向误差的计算参见上篇博文:Apollo代码学习(三)—车辆动力学模型。
代码中,matrix_state_为状态变量:
matrix_state_ = Matrix::Zero(matrix_size, 1);
matrix_state_(0, 0) = debug->lateral_error();
matrix_state_(1, 0) = debug->lateral_error_rate();
matrix_state_(2, 0) = debug->heading_error();
matrix_state_(3, 0) = debug->heading_error_rate();
对应的状态矩阵A,即代码中的matrix_a_
matrix_a_ = Matrix::Zero(basic_state_size_, basic_state_size_);
matrix_ad_ = Matrix::Zero(basic_state_size_, basic_state_size_);
matrix_adc_ = Matrix::Zero(matrix_size, matrix_size);
matrix_a_(0, 1) = 1.0;
matrix_a_(1, 2) = (cf_ + cr_) / mass_;
matrix_a_(2, 3) = 1.0;
matrix_a_(3, 2) = (lf_ * cf_ - lr_ * cr_) / iz_;
matrix_a_coeff_ = Matrix::Zero(matrix_size, matrix_size);
matrix_a_coeff_(1, 1) = -(cf_ + cr_) / mass_;
matrix_a_coeff_(1, 3) = (lr_ * cr_ - lf_ * cf_) / mass_;
matrix_a_coeff_(2, 3) = 1.0;
matrix_a_coeff_(3, 1) = (lr_ * cr_ - lf_ * cf_) / iz_;
matrix_a_coeff_(3, 3) = -1.0 * (lf_ * lf_ * cf_ + lr_ * lr_ * cr_) / iz_;
matrix_a_coeff_用于更新状态矩阵matrix_a_
void LatController::UpdateMatrix() {
const double v =
std::max(VehicleStateProvider::instance()->linear_velocity(), 0.2);
matrix_a_(1, 1) = matrix_a_coeff_(1, 1) / v;
matrix_a_(1, 3) = matrix_a_coeff_(1, 3) / v;
matrix_a_(3, 1) = matrix_a_coeff_(3, 1) / v;
matrix_a_(3, 3) = matrix_a_coeff_(3, 3) / v;
Matrix matrix_i = Matrix::Identity(matrix_a_.cols(), matrix_a_.cols());
matrix_ad_ = (matrix_i + ts_ * 0.5 * matrix_a_) *
(matrix_i - ts_ * 0.5 * matrix_a_).inverse();
}
matrix_adc_.block(0, 0, basic_state_size_, basic_state_size_) = matrix_ad_;
则状态矩阵matrix_a_为:
(7) m a t r i x _ a _ = [ 0 1 0 0 0 − C f + C r m V C f + C r m ℓ r C r − ℓ f C f m V 0 0 0 1 0 ℓ r C r − ℓ f C f I z V ℓ f C f − ℓ r C r I z ℓ r 2 C r − ℓ f 2 C f I z V ] matrix\_a\_ = \begin{bmatrix} 0 & 1 & 0 & 0 \\ 0 & -\frac{C_f+C_r}{mV} & \frac{C_f+C_r}{m} & \frac{\ell_rC_r-\ell_fC_f}{mV} \\ 0 & 0 & 0 & 1 \\ 0 & \frac{\ell_rC_r-\ell_fC_f}{I_zV} & \frac{\ell_fC_f-\ell_rC_r}{I_z} & \frac{\ell_r^2C_r-\ell_f^2C_f}{IzV} \end{bmatrix} \tag{7} matrix_a_=⎣⎢⎢⎢⎡00001−mVCf+Cr0IzVℓrCr−ℓfCf0mCf+Cr0IzℓfCf−ℓrCr0mVℓrCr−ℓfCf1IzVℓr2Cr−ℓf2Cf⎦⎥⎥⎥⎤(7)
由于动力学模型基于单车模型,它将左右两侧轮胎合并为一个轮胎,因此式中的转角刚度 C f 、 C r C_f、C_r Cf、Cr应为单边转角刚度的2倍,文中均如此。
与动力学模型中的公式24的首项系数吻合。在没有预估的情况下,matrix_adc_=matrix_ad_, matrix_ad_ 为离散时间下的状态矩阵,采用的是双线性变换离散法。感谢博友LLCCCJJ的友情提示。
控制矩阵B,即代码中的matrix_b_,matrix_bd_ 为离散时间下的控制矩阵:
matrix_b_ = Matrix::Zero(basic_state_size_, 1);
matrix_bd_ = Matrix::Zero(basic_state_size_, 1);
matrix_bdc_ = Matrix::Zero(matrix_size, 1);
matrix_b_(1, 0) = cf_ / mass_;
matrix_b_(3, 0) = lf_ * cf_ / iz_;
matrix_bd_ = matrix_b_ * ts_;
matrix_bdc_.block(0, 0, basic_state_size_, 1) = matrix_bd_;
(8) m a t r i x _ b _ = [ 0 c f m 0 ℓ f C f I z ] matrix\_b\_= \begin{bmatrix} 0 \\ \frac{c_f}{m} \\ 0 \\ \frac{\ell_fC_f}{I_z} \end{bmatrix} \tag{8} matrix_b_=⎣⎢⎢⎡0mcf0IzℓfCf⎦⎥⎥⎤(8)
与动力学模型中公式24的 δ \delta δ的系数吻合。在没有预估的情况下,matrix_bdc_=matrix_bd_。
对于控制系统,求其最优控制解的方法有很多,apollo用的是LQR调节器(可参考一下官方讲解视频:线性二次调节器),它求解的核心是设计一个能量函数,最优的控制轨迹应该使得该能量函数最小。能量函数的一般形式为:
(9) J = 1 2 ∫ 0 ∞ ( x T Q x + u T R u ) d t J=\frac{1}{2}\int_0^\infty (x^TQx+u^TRu)dt \tag{9} J=21∫0∞(xTQx+uTRu)dt(9)
其中, Q Q Q是半正定矩阵, R R R为正定矩阵,可自行设计。
设计LQR控制器,需要求取 K K K矩阵,计算反馈矩阵 K K K的过程:
- 选择参数矩阵 Q Q Q, R R R;
- 求解Riccati 方程得到矩阵 P P P;
- 计算 K = R − 1 B T P K=R^{-1}B^TP K=R−1BTP。
LQR的求解过程可参看LQR,感兴趣的可以研究一下,matlab、python等也提供的都有用于求解LQR模型的函数。
Apollo中对Q、R矩阵的定义如下:
lqr_eps_ = control_conf->lat_controller_conf().eps();
lqr_max_iteration_ = control_conf->lat_controller_conf().max_iteration();
query_relative_time_ = control_conf->query_relative_time();
matrix_k_ = Matrix::Zero(1, matrix_size);
matrix_r_ = Matrix::Identity(1, 1);
matrix_q_ = Matrix::Zero(matrix_size, matrix_size);
int q_param_size = control_conf->lat_controller_conf().matrix_q_size();
for (int i = 0; i < q_param_size; ++i) {
matrix_q_(i, i) = control_conf->lat_controller_conf().matrix_q(i);
}
matrix_q_updated_ = matrix_q_;
求取K矩阵的代码:
if (FLAGS_enable_gain_scheduler) {
matrix_q_updated_(0, 0) =
matrix_q_(0, 0) *
lat_err_interpolation_->Interpolate(
VehicleStateProvider::instance()->linear_velocity());
matrix_q_updated_(2, 2) =
matrix_q_(2, 2) *
heading_err_interpolation_->Interpolate(
VehicleStateProvider::instance()->linear_velocity());
common::math::SolveLQRProblem(matrix_adc_, matrix_bdc_, matrix_q_updated_,
matrix_r_, lqr_eps_, lqr_max_iteration_,
&matrix_k_);
} else {
common::math::SolveLQRProblem(matrix_adc_, matrix_bdc_, matrix_q_,
matrix_r_, lqr_eps_, lqr_max_iteration_,
&matrix_k_);
}
其中,状态变量matrix_state_、混合状态矩阵matrix_adc_、混合控制矩阵matrix_bdc_、增益矩阵matrix_k_是时变的,状态权重矩阵matrix_q_可能是时变的,控制权重矩阵matrix_r_、阈值lqr_eps_、最大迭代次数lqr_max_iteration_是固定的。
求出 K K K矩阵后,即可求最优控制解:
// feedback = - K * state
// Convert vehicle steer angle from rad to degree and then to steer degree
// then to 100% ratio
const double steer_angle_feedback = -(matrix_k_ * matrix_state_)(0, 0) * 180 /
M_PI * steer_transmission_ratio_ /
steer_single_direction_max_degree_ * 100;
const double steer_angle_feedforward = ComputeFeedForward(debug->curvature());
// Clamp the steer angle to -100.0 to 100.0
double steer_angle = common::math::Clamp(
steer_angle_feedback + steer_angle_feedforward, -100.0, 100.0);
总结
本文详述了Apollo的横纵向控制,纵向控制的主体是PID控制,横向控制的主体是前馈控制器加反馈控制器,反馈控制器的设计依赖于LQR模型;Apollo中的MPC基于横纵向控制设计。
由于对线性化、离散化等知识理解有限,故在此篇中未对LQR的求解做展开说明,下篇文章将尝试对非线性系统的线性化、求最优解等进行分析。
补充 2018.11.28
很多人(包括我)对于横向误差 l a t e r a l _ e r r o r lateral\_error lateral_error和纵向误差中的位误差 s t a t i o n _ e r r o r station\_error station_error的计算不太明白,我就试着去解释一下吧。
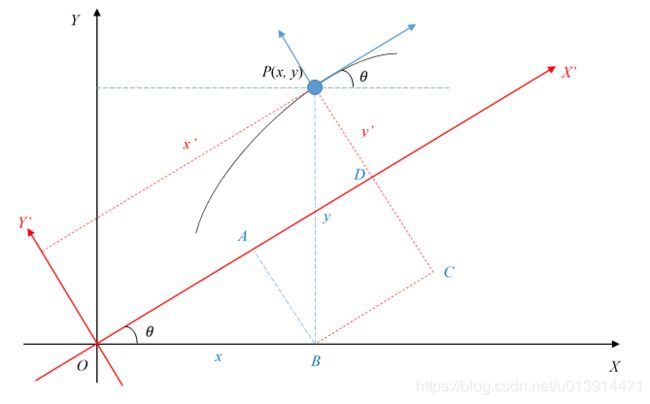
首先,对于坐标系下任一点 ( x , y ) (x,y) (x,y),假设如图6所示,将坐标轴绕原点向左旋转 θ \theta θ角度后的坐标值 ( x ′ , y ′ ) (x',y') (x′,y′)满足以下等式:
(10) { x ′ = O A + B C = x cos θ + y sin θ y ′ = P C − A B = y cos θ − x sin θ \begin{cases} x'=OA+BC=x\cos{\theta}+y\sin{\theta}\\ y'=PC-AB=y\cos{\theta}-x\sin{\theta} \end{cases}\tag{10} {x′=OA+BC=xcosθ+ysinθy′=PC−AB=ycosθ−xsinθ(10)
可自行推广到其他角度或象限的旋转。坐标系旋转可参考博客:二维坐标系的转换。
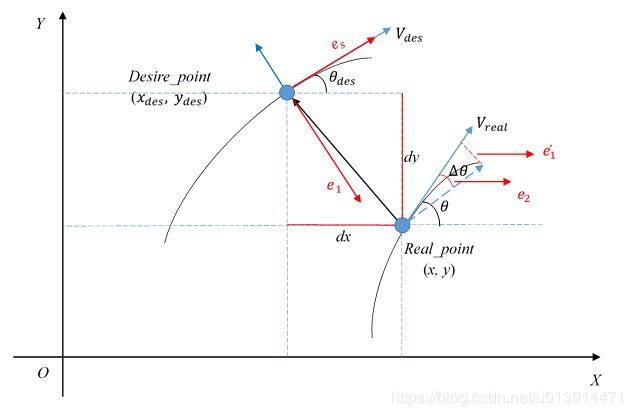
结合图3和代码中的注释,可得图7,其中 V d e s V_{des} Vdes垂直于 e 1 e_1 e1, e s e_s es为位置误差 s t a t i o n _ e r r o r station\_error station_error, e 1 e_1 e1为横向误差 l a t e r a l _ e r r o r lateral\_error lateral_error。
首先,在笛卡尔坐标系中,参考点与真实点间在X、Y轴方向的误差:
d x = x − x d e s , d y = y − y d e s dx=x-x_{des},dy=y-y_{des} dx=x−xdes,dy=y−ydes
可参看代码,横纵向代码表述有异,但殊途同归:
// 纵向控制
double dx = x - ref_point.x();
double dy = y - ref_point.y();
double cos_ref_theta = std::cos(ref_point.theta());
double sin_ref_theta = std::sin(ref_point.theta());
// 横向控制
const double dx = x - target_point.path_point().x();
const double dy = y - target_point.path_point().y();
const double cos_matched_theta = std::cos(target_point.path_point().theta());
const double sin_matched_theta = std::sin(target_point.path_point().theta());
为什么 d x , d y dx,dy dx,dy是实际点坐标减去参考点坐标?
个人理解: 控制的目的是为了将车辆从当前点移动到期望点,分别在 x , y x,y x,y方向上移动 d x , d y dx,dy dx,dy的距离能到参考点,所以 d x , d y dx,dy dx,dy是实际点坐标减去参考点坐标。
而怎么从规划轨迹中找对应的参考点,有两种方法, 根据绝对时间或者位置最近进行匹配,
TrajectoryPoint target_point;
// 绝对时间
target_point = trajectory_analyzer.QueryNearestPointByAbsoluteTime(
current_timestamp + query_relative_time_);
// 相对位置
target_point = trajectory_analyzer.QueryNearestPointByPosition(x, y);
按照最近位置寻找匹配点的话,找的其实就是参考点与实际点间连线距离最短的参考点。但这个连线距离最短中的距离,指的不是横向误差,也不是纵向误差,而是两点间连线的长度
d i s t a n c e = d x 2 + d y 2 distance=\sqrt{dx^2+dy^2} distance=dx2+dy2
计算横纵向误差是在S-L坐标系下,而 d x , d y dx,dy dx,dy是在笛卡尔坐标系下计算的,因此需要进行坐标系转换,简单的来说就是将原始坐标系进行旋转,使其与S-L坐标系重合,如图6所示。且坐标系旋转后,参考点与实际点两点间距离 d i s t a n c e distance distance应是不变的。
为什么将参考点进行旋转,而不是将实际点进行旋转?
个人理解: 控制的目的是为了让汽车按照规划轨迹行驶,当前时刻的误差,肯定是基于参考点得来的,也就是我要找到现在实际的点相较于参考点,在横纵方向上的误差各是多少。因此横纵向误差的计算中的角度使用的期望航向角 θ d e s \theta_{des} θdes。
对于纵向误差的计算,可见代码trajectory_analyzer.cc以及lon_controller.cc:
// the sin of diff angle between vector (cos_ref_theta, sin_ref_theta) and
// (dx, dy)
double cross_rd_nd = cos_ref_theta * dy - sin_ref_theta * dx;
*ptr_d = cross_rd_nd;
// the cos of diff angle between vector (cos_ref_theta, sin_ref_theta) and
// (dx, dy)
double dot_rd_nd = dx * cos_ref_theta + dy * sin_ref_theta;
*ptr_s = ref_point.s() + dot_rd_nd;
double delta_theta = theta - ref_point.theta();
double cos_delta_theta = std::cos(delta_theta);
double sin_delta_theta = std::sin(delta_theta);
*ptr_d_dot = v * sin_delta_theta;
double one_minus_kappa_r_d = 1 - ref_point.kappa() * (*ptr_d);
if (one_minus_kappa_r_d <= 0.0) {
AERROR << "TrajectoryAnalyzer::ToTrajectoryFrame "
"found fatal reference and actual difference. "
"Control output might be unstable:"
<< " ref_point.kappa:" << ref_point.kappa()
<< " ref_point.x:" << ref_point.x()
<< " ref_point.y:" << ref_point.y() << " car x:" << x
<< " car y:" << y << " *ptr_d:" << *ptr_d
<< " one_minus_kappa_r_d:" << one_minus_kappa_r_d;
// currently set to a small value to avoid control crash.
one_minus_kappa_r_d = 0.01;
}
*ptr_s_dot = v * cos_delta_theta / one_minus_kappa_r_d;
// 位置误差, 其中s_matched = ptr_s
debug->set_station_error(reference_point.path_point().s() - s_matched);
// 速度误差, 其中s_dot_matched = ptr_s_dot
debug->set_speed_error(reference_point.v() - s_dot_matched);
纵向位置误差 s t a t i o n _ e r r o r station\_error station_error为
(11) s t a t i o n _ e r r o r = − ( d x ∗ cos θ d e s + d y ∗ sin θ d e s ) station\_error=-(dx*\cos{\theta_{des}+dy*\sin{\theta_{des}}}) \tag{11} station_error=−(dx∗cosθdes+dy∗sinθdes)(11)
对于横向误差的计算,可见代码lat_controller.cc:
const double cos_target_heading = std::cos(target_point.path_point().theta());
const double sin_target_heading = std::sin(target_point.path_point().theta());
double lateral_error = cos_target_heading * dy - sin_target_heading * dx;
if (FLAGS_enable_navigation_mode_error_filter) {
lateral_error = lateral_error_filter_.Update(lateral_error);
}
debug->set_lateral_error(lateral_error);
也就是:
(12) l a t e r a l _ e r r o r = d y ∗ cos θ d e s − d x ∗ sin θ d e s lateral\_error=dy*\cos{\theta_{des}}-dx*\sin{\theta_{des}} \tag{12} lateral_error=dy∗cosθdes−dx∗sinθdes(12)
结合公式10、公式11、公式12, s t a t i o n _ e r r o r , l a t e r a l _ e r r o r station\_error,lateral\_error station_error,lateral_error分别和 x ′ , y ′ x',y' x′,y′的绝对值相等。且满足坐标系旋转过后,参考点和实际点间的直线距离是不变的规律:
(13) d i s t a n c e = d x 2 + d y 2 = s t a t i o n _ e r r o r 2 + l a t e r a l _ e r r o r 2 distance=\sqrt{dx^2+dy^2}=\sqrt{station\_error^2+lateral\_error^2}\tag{13} distance=dx2+dy2=station_error2+lateral_error2(13)