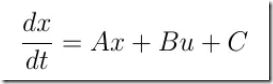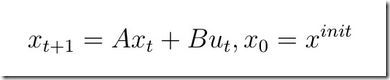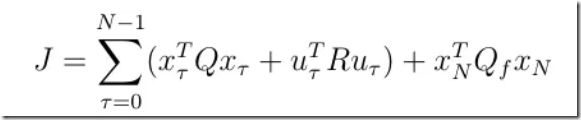开发者说 | Apollo控制算法之汽车动力学模型和LQR控制

参考：https://mp.weixin.qq.com/s?__biz=MzI1NjkxOTMyNQ==&mid=2247486444&idx=1&sn=6538bf1fa74429600d8fa10f4f766a58&chksm=ea1e199edd699088aee4b3c72404649751c60a9901ab71421f64e7125759765193bb4827aa15&scene=0&xtrack=1#rd

 

https://mp.weixin.qq.com/s?__biz=MzI1NjkxOTMyNQ==&mid=2247486554&idx=1&sn=4e3655d0adf0ba126b49d03df63bc64a&chksm=ea1e1e28dd69973eab7f08b2c520d4258877a7dcff8533646d2282bf5cb98a7999e9794a236f&scene=0&xtrack=1#rd

 

动力学主要研究作用于物体的力与物体运动的关系。

 

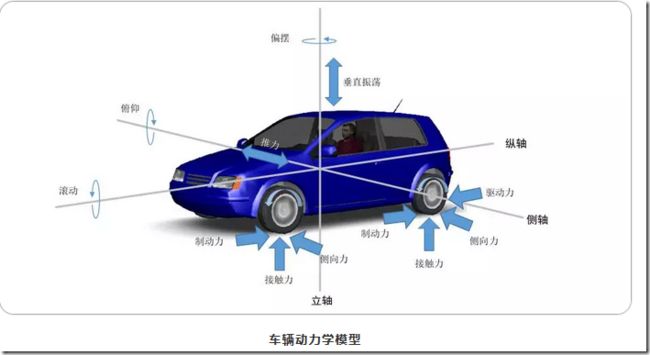
车辆动力学模型一般用于分析车辆的平顺性和车辆操纵的稳定性。

对于车来说，研究车辆动力学，主要是研究车辆轮胎及其相关部件的受力情况。

比如纵向速度控制，通过控制轮胎转速实现；

横向航向控制，通过控制轮胎转角实现。

正常情况下，车辆上的作用力沿着三个不同的轴分布：

纵轴上的力包括驱动力和制动力，以及滚动阻力和拖拽阻力作滚摆运动；

横轴上的力包括转向力、离心力和侧风力，汽车绕横轴作俯仰运动；

立轴上的力包括车辆上下振荡施加的力，汽车绕立轴作偏摆或转向运动。

无论是LQR或是MPC控制，都需要有车辆的模型作为基础。

动力学模型

• 小角度侧偏角

• 匀速

• 不考虑环境因素

   

  

   

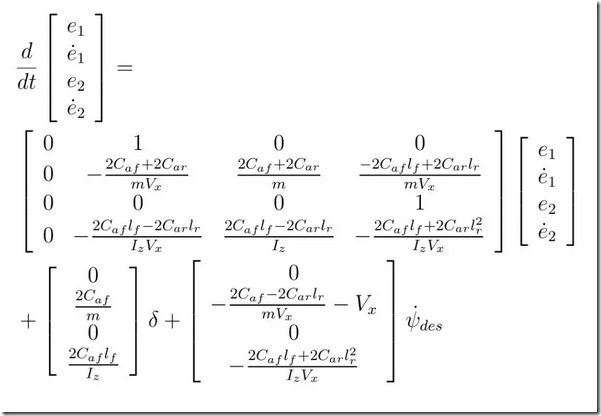
• 设e1为横向偏差，e2为航向角偏差，

  进而得：

  

  其中

  

  

• 

  其中：

  

  

  

  ---

  LQR 理论是现代控制理论中发展最早也最为成熟的一种状态空间设计法。特别可贵的是，LQR可得到状态线性反馈的最优控制规律，易于构成闭环最优控制。

  LQR 最优设计是指设计出的状态反馈控制器 K 要使二次型目标函数 J 取最小值，而 K 由权矩阵 Q 与 R 唯一决定，故此 Q、R 的选择尤为重要。

  而且 Matlab 的应用为 LQR 理论仿真提供了条件，更为我们实现稳、准、快的控制目标提供了方便。

  

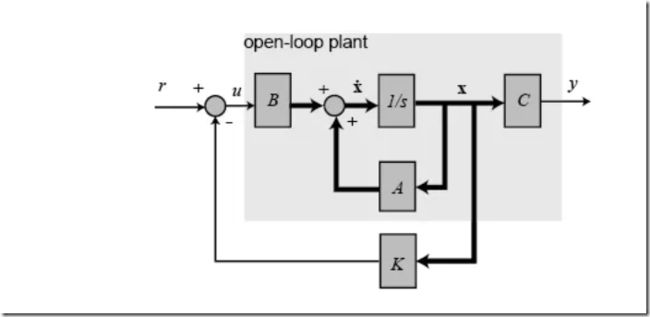
  线性二次调节器（Linear Quadratic Regulator 或LQR）是基于模型的控制器，它使用车辆的状态来使误差最小化。

  Apollo 使用 LQR 进行横向控制。横向控制包含四个组件：

  横向误差

  横向误差的变化率

  朝向误差

  朝向误差的变化率

  变化率与导数相同，我们用变量名上面的一个点来代表。

  我们称这四个组件的集合为X，这个集合X捕获车辆的状态。除了状态之外，该车有三个控制输入：转向、加速和制动。我们将这个控制输入集合称为U。

  我们考虑有如下离散线性系统：

  

   

  为了达到上述效果，定义代价函数：

  

  其中x为状态量，u为控制量，Q为状态权重矩阵，R为控制权重矩阵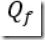，为最终状态权重矩阵，N为到达最终状态的控制序列数。

   

  

  

  其中K即为通过迭代求解黎卡提方程得到的等效闭环反馈矩阵。

  至此，LQR算法求解过程可以总结为：

  1. 令P等于最终状态权重矩阵;

  2. 迭代黎卡提方程求出新的P;

  3. 当两次P的差值足够小时，计算反馈矩阵K;

  4. 根据反馈矩阵K获取最优控制量u；

  采用《Apollo控制算法之汽车动力学模型》一文中的模型，代入AD、BD、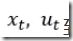到以上算法对应各项，因模型中的CD项为常量，在LQR求解完成后加入即可获得最终所需的系统控制量。

 

 

另外参见：

https://blog.csdn.net/heyijia0327/article/details/39270597

 

转载于:https://www.cnblogs.com/mohuishou-love/p/10475029.html