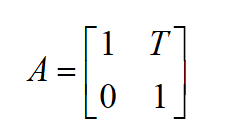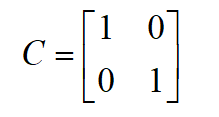模型预测控制系列讲解（一）：抛砖引玉（自动驾驶车辆纵向控制实例）

1.说明

首先通过一个简单的基于恒加速度（CA）车辆运动学模型MPC控制算法，引出模型预测控制，可以对模型预测控制有提个初步的感性的认知，具体模型预测控制思想，实现方式，实现步骤，定量分析，定性分析，性能指标设计以及参数整定等等后续会持续更新相关内容，可以先按照该篇模型先行仿真，感受模型预测控制。

2.模型预测控制实现

2.1预测模型构建

恒加速度（CA）模型（高中物理），已经离散化后的线性模型：

其中：
$v_k$ 为 $k$时刻车辆速度,
$v_{k+1}$为$k+1$时刻车辆速度，
$a_k$ 为 $k$ 时刻车辆加速度，
$d_k$ 为 $k$ 时刻车辆位置，
$d_{k+1}$为$k+1$时刻车辆位置，
$T$ 为 采样时间。
将上述模型写成矩阵形式：

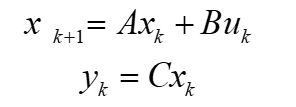
其中：
$x_k=[d_k,v_k{]}^T$，为状态向量，
$u_k=a_k$，为控制量，
$y_k=[d_k,v_k{]}^T$，为输出向量，
$A,B,C$分别为状态矩阵，控制矩阵，输出矩阵。
由上述模型可以求得A,B,C:

2.2性能指标要求及设计

在设计性能指标的时候考虑因素：
1.输出与期望偏差尽可能小，反映系统跟随能力
2.尽量对控制量的突变情况进行约束，所以采用控制增量来约束
具体性能指标形式如下：
$J(k)={\sum }_{i=1}^{Np}||y_{real}(k+i/k)-y_{des}(k+i/k)|{|}_{Q\_base}^2+{\sum }_{i=0}^{Nc-1}||\Delta u(k+i/k)|{|}_{R\_base}^2$
性能指标的选取与实际需求有着非常紧密的联系，通常会先选择性能指标，再根据性能指标来决定预测模型的选取或者建立。

2.3根据性能指标要求重构预测模型

根据性能指标，将预测模型重构成含有控制增量的方式，重构方法：待定系数法，具体形式如下：
$$\begin{gathered} {\xi }_{k+1}=A_{tran}{\xi }_k+B_{tran}\Delta u_k \\ {y}_k=C_{tran}{\xi }_k \end{gathered}$$

$\Delta u_k=u_k-u_{k-1}$；
${\xi }_k=[d_k,v_k,a_{k-1}{]}^T$；
可以求得$A_{tran}$，$B_{tran}$，$C_{tran}$
$A_{tran}=[1,T,T^2/2;0,1,T;0,0,1]$；
$B_{tran}=[T^2/2;T;1]$；
$C_{tran}=[1,0,0;0,1,0]$；
性能指标可以写的更紧凑：
$J(k)=||Y(t)-Y_{des}(t)|{|}_Q^2+||\Delta u(t)|{|}_R^2$
其中：
$Y(t)=[y_{(}k+1/k),y(k+2/k),...,y(k+Np/k){]}^T$；
$Y_{des}(t)=[y_{des}(k+1/k),y_{des}(k+2/k),...,y_{des}(k+Np/k){]}^T$；
$\Delta u(t)=[\Delta u(k),\Delta u(k+1),...,\Delta u(k+Nc-1){]}^T$；
$Q$的对角线上的元素为$Q_{base}(k+1)，Q_{base}(k+2),...Q_{base}(k+Np)$
$R$的对角线上的元素为$R_{base}(k),R_{base}(k+1),...,R_{base}(k+Nc-1)$；
具体实现大家可以亲自推导一遍，在推导过程用分块矩阵去做，以预测时域和控制时域来分块，便于推导和理解。

2.4根据预测模型预测Np时域内系统输出

预测时域Np内的系统输出可以在当前状态下通过预测模型得到，并且只与当前状态$x(k)$和未来控制时域Nc的控制量$u(k),u(k+1),...,u(k+Nc-1)$有关，而未来Nc时域的控制量又可以由前一时刻的控制量$u(k-1)$和$\Delta u(k),\Delta u(k+1),...,\Delta u(k+Nc-1)$来计算的来，具体推导大家可以亲手试着推导一遍，更容易理解其中的变换过程，这里就不再进行推导。
用紧凑型来表示：
$Y(t)=\Phi {\xi }_k+\Theta \Delta u(t)$
其中，$Y(t),{\xi }_k,\Delta u(t)$上面已经列出，重点是$\Phi ,\Theta$的计算，可以选取Np和Nc都小一点，推导一下，规律很好找，由于公式编辑是在太过耗时，这里不再展开，大家可以在代码中看到具体形式，或者参考北理工出版的《无人驾驶车辆模型预测控制》。

2.5约束条件设计

约束条件，根据被控量物理属性，控制过程的舒适性等等来设计，具体如何设计会在后续详细分一章节来展开。
首先，对控制量的约束：
$u_{min}(t)<=u(t)<=u_{max}(t)$
$u(t)=[u(k),u(k+1),...,u(k+Nc-1){]}^T$；
再次，对控制增量的约束：
$\Delta u_{min}(t)<=\Delta u(t)<=\Delta u_{max}(t)$
$\Delta u(t)=[\Delta u(k),\Delta u(k+1),...,\Delta u(k+Nc-1){]}^T$；
具体限制值代码中会给出，由于求解变量为控制增量，所以需要将约束条件转换成只含有控制增量的表达式：
$$\begin{gathered} \Delta U_{min}(t)<=\Delta U(t)<=\Delta U_{max}(t) \\ {U}_{min}(t)<=A_c\Delta U(t)+U(k-1)<=U_{max}(t) \end{gathered}$$
其中所有含有大写U都是Nc控制时域内的对应值，都是Nc*size(u)的列向量
$U(k-1)$为Nc长度的列向量与$u(k-1)$的克罗内克积，
$A_c$为下三角元素全为1，$Nc\ast Nc$的对角矩阵与$I_{Nu}$的克罗内克积。
$A_c\Delta U(t)+U(k-1)$目的就是由未来Nc个时刻的控制增量和上一时刻的控制量来计算未来Nc个时刻的控制量。

2.6整理化简性能指标为标准二次规划形式

就是将前面的性能指标通过矩阵的性质，化简为标准的二次规划形式，就可以使用quadprog来求解，大家可以通过matlab的帮助文档来获得二次规划函数quadprog的实际使用方法，以及参数传递，文档中会有标准二次规划的说明。

	% 性能指标转化为标准二次规划系数矩阵
	H = Theta' * Q * Theta + R;
	H = (H + H')/2;
	f = (2*(Phi * kesi - y_ref)' * Q * Theta)';

这里是转换结果，推导过程大家可以体验一下，后续我会把手动推导的过程以图片的形式贴上来。

3.仿真结果

仿真的数据输入是根据CA（横加速度）模型，根据采样时间，以一个恒定的加速度来计算出期望速度和期望位置，给入模型预测控制，简单的仿真曲线，大概可以反应控制效果，具体可以修改其中的权值，预测时域以及控制时域来优化控制效果。
速度跟随曲线：

位置跟随曲线：

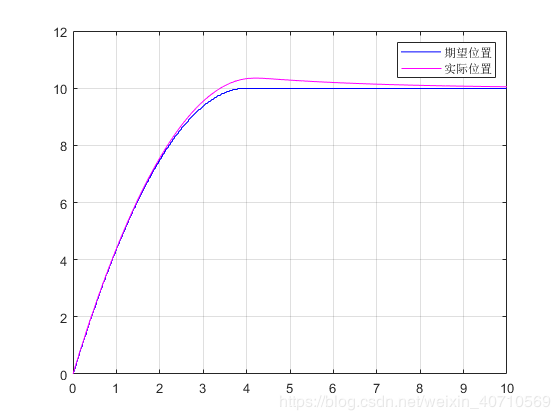
如果输入期望值直接给入阶跃值，效果又如何？造成这样的原因是什么，在不改变期望输入的情况下，怎么解决？我会在接下来的更新过程中说明一些解决方案。这也是需要加速度规划和不需要加速度规划的问题，其实这两种情况我们实际应用中是都会遇到的，之后我会详细为大家说明。

4.总结

这个只是使用非常简单的预测模型，没有太多复杂处理，只用来大家体验下模型预测控制的实现，对MPC有一个初步的认知。
接下来会展开来讲模型预测控制的相关原理，思想方式，不同的实现方式，简单的稳定性分析，定量以及定性的分析等等。会在后续介绍中，介绍已经经过RCP(快速原型)验证的基于MPC的ACC(自适应巡航)控制算法，详细介绍性能指标的选取，参数的调节等等。

5.S_Function代码（后续会更新C/C++代码）

下面附MPC的S_Function代码：
该代码是在Matlab2018b中开发

function MPC_long_control(block)
% Level-2 MATLAB file S-Function
% 基于恒加速度汽车纵向模型的模型预测控制
	setup(block);
% endfunction
function setup(block)

	% Register number of ports
	block.NumInputPorts  = 4;
	block.NumOutputPorts = 2;

	% setup port properties to be inherited or dynamic
	block.SetPreCompInpPortInfoToDynamic;
	block.SetPreCompOutPortInfoToDynamic;

	% Override input port properties
	block.InputPort(1).Dimensions = 1;
	block.InputPort(1).DatatypeID = 0;    % double
	block.InputPort(1).Complexity = 'Real';
	block.InputPort(1).DirectFeedthrough = false;
	block.InputPort(1).SamplingMode = 'Sample';

	block.InputPort(2).Dimensions = 1;
	block.InputPort(2).DatatypeID = 0;    % double
	block.InputPort(2).Complexity = 'Real';
	block.InputPort(2).DirectFeedthrough = false;
	block.InputPort(2).SamplingMode = 'Sample';

	block.InputPort(3).Dimensions = 1;
	block.InputPort(3).DatatypeID = 0;    % double
	block.InputPort(3).Complexity = 'Real';
	block.InputPort(3).DirectFeedthrough = false;
	block.InputPort(3).SamplingMode = 'Sample';

	block.InputPort(4).Dimensions = 1;
	block.InputPort(4).DatatypeID = 0;    % double
	block.InputPort(4).Complexity = 'Real';
	block.InputPort(4).DirectFeedthrough = false;
	block.InputPort(4).SamplingMode = 'Sample';

	% Override output port properties
	block.OutputPort(1).Dimensions = 1;
	block.OutputPort(1).DatatypeID = 0;    % double
	block.OutputPort(1).Complexity = 'Real';
	block.OutputPort(1).SamplingMode = 'Sample';

	block.OutputPort(2).Dimensions = [1,2];
	block.OutputPort(2).DatatypeID = 0;    % double
	block.OutputPort(2).Complexity = 'Real';
	block.OutputPort(2).SamplingMode = 'Sample';

	% Register parameters
	block.NumDialogPrms = 2;
	block.DialogPrmsTunable = {'Tunable','Tunable'};

	block.SampleTimes = [-1,0];
	block.SimStateCompliance = 'DefaultSimState';

	block.RegBlockMethod('PostPropagationSetup', @DoPostPropSetup);
	block.RegBlockMethod('InitializeConditions', @InitializeConditions);
	block.RegBlockMethod('Outputs', @Outputs);
	block.RegBlockMethod('Update', @Update);

% end setup
function DoPostPropSetup(block)
	% 系统状态变量设置
	% 状态变量个数设置
	block.NumDworks = 2;

	block.Dwork(1).Name            = 'd_rel';
	block.Dwork(1).Dimensions      = 1;
	block.Dwork(1).DatatypeId      = 0;    %double
	block.Dwork(1).Complexity      = 'Real';
	block.Dwork(1).UsedAsDiscState = true;

	block.Dwork(2).Name            = 'v_rel';
	block.Dwork(2).Dimensions      = 1;
	block.Dwork(2).DatatypeId      = 0;    %double
	block.Dwork(2).Complexity      = 'Real';
	block.Dwork(2).UsedAsDiscState = true;

% end DoPostPropSetup
function InitializeConditions(block)
	% 初始化设置
	global U;    % 控制量
	U = 0;
	block.Dwork(1).Data = block.DialogPrm(1).Data;
	block.Dwork(2).Data = block.DialogPrm(2).Data;

% end InitializeConditions

function Outputs(block)
	% 输出函数
	global U;
	Ts  = 0.01;   % 采样周期
	Np  = 50;     % 预测时域
	Nc  = 50;     % 控制时域
	Row = 10;     % 松弛因子
	Nx  = 2;      % 状态量个数
	Nu  = 1;      % 控制量个数
	No  = 2;      % 输出量个数

	% 控制期望值计算以及转换
	y_des = [block.InputPort(1).Data, block.InputPort(2).Data]';    % 期望输出向量
	y_ref = kron(ones(Np, 1), y_des);                               % 预测时域内各时刻期望输出

	% 预测状态方程状态向量计算
	vector_x = [block.Dwork(1).Data, block.Dwork(2).Data]';              % 原始状态方程状态向量
	Kesi_cell = cell(2, 1);
	Kesi_cell{1,1} = vector_x;
	Kesi_cell{2,1} = U;
	kesi = cell2mat(Kesi_cell);                                   % 预测状态方程状态向量

	% 初始状态方程矩阵以及输出矩阵
	A = [1,Ts;0,1];
	B = [(Ts^2)/2,Ts]';
	C = eye(2);

	% 变换后状态方程系数矩阵
	A_tran_cell = cell(2,2);
	B_tran_cell = cell(2,1);
	C_tran_cell = cell(1,2);
	A_tran_cell{1,1} = A;
	A_tran_cell{1,2} = B;
	A_tran_cell{2,1} = zeros(Nu,Nx);
	A_tran_cell{2,2} = eye(Nu);
	B_tran_cell{1,1} = B;
	B_tran_cell{2,1} = eye(Nu);
	C_tran_cell{1,1} = C;
	C_tran_cell{1,2} = zeros(No,1);
	A_tran = cell2mat(A_tran_cell);
	B_tran = cell2mat(B_tran_cell);
	C_tran = cell2mat(C_tran_cell);

	% 系统预测输出系数矩阵
	Phi_cell    = cell(Np,1);
	Theta_cell  = cell(Np,Nc);
	for i = 1:Np
		Phi_cell{i,1} = C_tran*(A_tran^i);
		for j = 1:Nc
			if j <= i
				Theta_cell{i,j} = C_tran*A_tran^(i-j)*B_tran;
			else
				Theta_cell{i,j} = zeros(No,Nu);
			end
		end
	end
	Phi   = cell2mat(Phi_cell);
	Theta = cell2mat(Theta_cell);

	% 性能指标权系数矩阵
	Q_base = [1,0;0,1];    % No*No的对角矩阵，输出误差基准加权矩阵
	R_base = 1;            % Nu*Nu的对角矩阵，控制量加权基准矩阵，此处为控制增量加权基准矩阵
	Q = eye(Np);
	R = eye(Nc);
	Q = kron(Q,Q_base);    % 预测时域内输出误差权矩阵
	R = kron(R,R_base);    % 控制时域内控制增量权矩阵

	% 性能指标转化为标准二次规划系数矩阵
	H = 2 * (Theta' * Q * Theta + R);
	H = (H + H')/2;
	f = (2*(Phi * kesi - y_ref)' * Q * Theta)';

	% 约束条件
	A_c  = tril(ones(Nc*Nu));
	Ut   = kron(ones(Nc,1),U);
	umin = -5;                        % 控制量最大值，此处为加速度最小值
	umax = 2;                         % 控制量最小值，此处为加速度最大值
	delta_umin = -0.05;               % 控制增量最小值
	delta_umax = 0.05;                % 控制增量最大值
	U_min = kron(ones(Nc,1),umin);
	U_max = kron(ones(Nc,1),umax);
	delta_Umin = kron(ones(Nc,1),delta_umin);
	delta_Umax = kron(ones(Nc,1),delta_umax);
	lb = delta_Umin;
	ub = delta_Umax;

	% 不等式约束系数矩阵
	A_con_cell = {A_c;-A_c};
	b_con_cell = {U_max - Ut;-U_min + Ut};
	A_con = cell2mat(A_con_cell);
	b_con = cell2mat(b_con_cell);

	% 二次规划求解
	options = optimset('Algorithm','');
	[X,fval,exitflag] = quadprog(H,f,A_con,b_con,[],[],lb,ub,[],options);

	% 控制量计算
	delta_u = X(1);
	U = U + delta_u;
	u_ctr = U;

	block.OutputPort(1).Data = u_ctr;
	block.OutputPort(2).Data = [u_ctr, delta_u];

% end Outputs
function Update(block)
	% 状态更新
	block.Dwork(1).Data = block.InputPort(3).Data;
	block.Dwork(2).Data = block.InputPort(4).Data;

% end Updata

补充1：性能指标转化成标准二次规划推导过程（手动推导）

这个推导过程看似复杂，经常在这会劝退很多人，实则掌握了它的本质，则就相对简单很多，要有一中持之以恒的信念！

性能指标：$$J(k)=||Y(t)-Y_{des}(t)|{|}_Q^2+||\Delta u(t)|{|}_R^2$$

输出预测方程：$$Y(t)=\Phi {\xi }_k+\Theta \Delta u(t)$$

标准二次规划形式：

$$\begin{array}{c}\underset{x}{\min }\frac{1}{2}{x}^{T}Hx+f^{T}x\\ st.\{\begin{array}{l}Ax⩽b\\ Aeq⩽beq\\ lb⩽x⩽ub\end{array}\end{array}$$
目标是将性能指标化简为标准二次规划形式。
推导过程中用到的矩阵运算性质：
$$\begin{array}{c}\{\begin{array}{l}(AB{)}^T=B^T{A}^T\\ (A\pm B{)}^T=A^T\pm B^T\\ ABC=A(BC)=(AB)C\\ A(B+C)=AB+AC\\ (B+C)A=BA+BC\end{array}\end{array}$$
当A矩阵为对称矩阵或者A为一个实数，则有：
$$A^T=A$$
这个性质在推导过程中及其重要，尤其是它的不同表现形式，如$M=AB$，如果我们知道M为对称矩阵或者M为实数，则会有：
$$\begin{array}{c}M=M^T=(AB{)}^T=B^T{A}^T\end{array}$$
下面是手动推导过程：
手动推导过程。

补充2：性能指标转化成标准二次规划推导过程（公式编辑）

这里采用公式编辑来跟清晰的展现转化过程。

其中$(\Phi {\xi }_k{)}^{T}Q(\Phi {\xi }_k)$和$2Y_{des}^T(t)Q(\Phi {\xi }_k)$，不含有优化变量$\Delta u(t)$，这两项可以看作是常数项，对优化不产生影响，比如要求$f(x)$的最小值：
$$\begin{array}{c}\underset{x}{\min }f(x)=f_1(x)+a\end{array}$$
式中$a$为常数项，那么$f(x)$取的最小值的时候就是$f_1(x)$取得最小值的时候。
所以最后的性能指标就可以简化为：
$$J(k)=\Delta u^T(t)({\Theta }^{T}Q\Theta +R)\Delta u(t)+2(\Phi {\xi }_k-Y_{des}(t){)}^{T}Q\Theta \Delta u(t)$$
对照上边的标准二次规划，可以得到其系数：
$$\begin{gathered} H=2({\Theta }^{T}Q\Theta +R) \\ f=(2(\Phi {\xi }_k-Y_{des}(t){)}^{T}Q\Theta {)}^T \end{gathered}$$
从而实现了从性能指标到标准二次规划的化简。