matlab时频分析之短时傅里叶变换 spectrogram

matlab时频分析之短时傅里叶变换 spectrogram

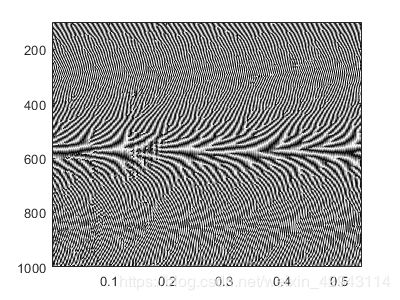
短时傅里叶变换常用于缓慢时变信号的频谱分析，可以观察沿时间变化的频谱信号。

其优点如下图所示，弥补了频谱分析中不能观察时间的缺点，也弥补了时域分析不能获取频率的缺点。

1 STFT的基本原理

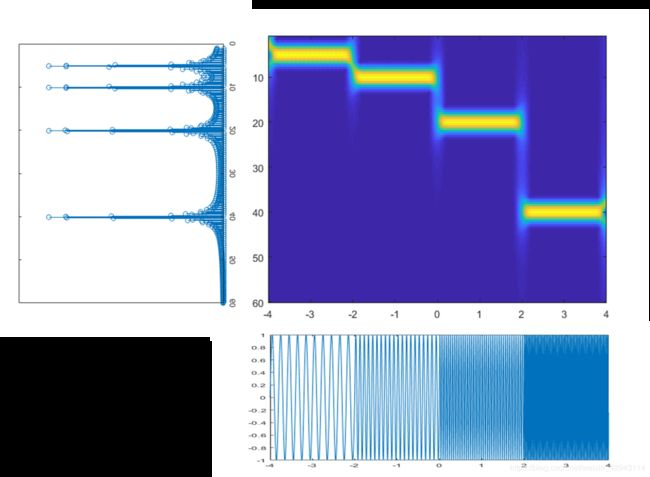
基本原理可以理解为对一段长信号，截取每一段时间的短信号做fft，将得到的频谱图时间沿时间轴排列，及可得到时频的云图。

2 matlab中实现

这里采用最基础的spectrogram函数作为分析函数。虽然在其它很多地方都能找到能实现更高级用法的函数，比如逆变换：
https://ww2.mathworks.cn/matlabcentral/fileexchange/45577-inverse-short-time-fourier-transform-istft-with-matlab
但是这里只是单纯的做可视化分析。

代码如下：

%短时傅里叶变换展示
fs=2^10;    %采样频率 fs=65536hz
dt=1/fs;    %时间精度
timestart=-4;
timeend=4;
t=(0:(timeend-timestart)/dt-1)*dt+timestart;
L=length(t);

%设置信号
z=sin(2*pi*5.*t).*(t<-2)+sin(2*pi*10.*t).*(t>=-2&t<0)+...
    sin(2*pi*20.*t).*(t>=0&t<2)+sin(2*pi*40.*t).*(t>=2);
z2=wextend(1,'sym',z,round(length(z)/2));%镜像延拓

wlen=512;%设置窗口长度。窗口越长时间分辨率越差，频率分辨率越好。
hop=1;%每次平移的步长，最小为1。越小图像时间精度越好，但计算量大。
z2=wkeep1(z2,L+1*wlen);%中间截断


%做短时傅里叶
h=hamming(wlen);%设置海明窗的窗长
f=1:0.5:60;%设置频率刻度

[tfr2,f,t2]=spectrogram(z2,h,wlen-hop,f,fs);
tfr2=tfr2*2/wlen*2;
figure
imagesc(t2+timestart-wlen/fs/2,f,abs(tfr2))

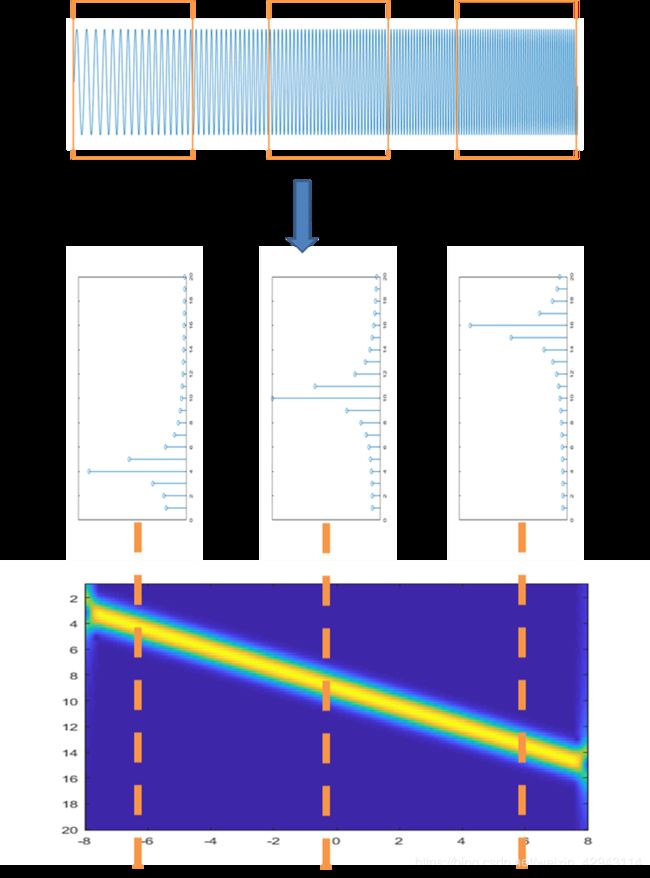
3 窗口长度与分辨率

短时傅里叶变换的分辨率和窗口长度wlen的选取，频率的刻度f、平移的步长hop都有关系。

spectrogram函数可以选取较密的频率刻度来增加频域的分辨率，减小平移步长增加时间的分辨率。

但是对于短时傅里叶变换，最重要的还是窗口长度的选取。当频域刻度和平移步长足够密时，增加的只是生成图像的大小，但是物理层面的分辨率却没有改变。改变物理层面分辨率的就是窗口长度。

下图为同一个信号，选取不同窗口长度的图像。其余量不变。

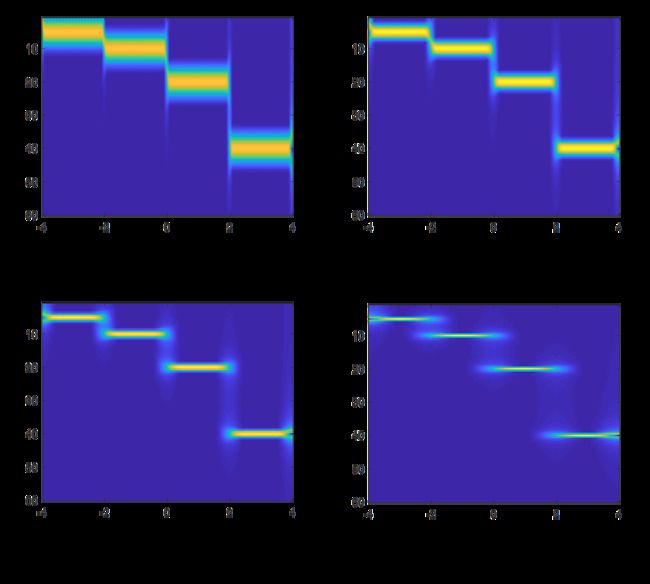
窗口长度大的话，比如2048，频率能够清晰的显示出来，但是时间上有些模糊。窗口长度比较小比如256，时间上的分界线能够清晰显示，但是频率的值却不能清晰读出。

这就是窗口的影响。可以想象，当窗口大到整个信号长度时，短时傅里叶变换就退化为傅里叶变换，没有时间维度。当窗口小到单个采样点时，分析也就退化为时域分析，无法做频域分析。

4 提高频率分辨率的方法

matlab中的spectrogram函数自带两种提高频率分辨率的方法。

第一种是利用功率谱，将能量集中的原理，提高频率分辨率。
用法为：
spectrogram(x,window,noverlap,f,fs,‘reassigned’,‘yaxis’);
前面的同第2节例子，在后面增加了’reassigned’选项。但是这个选项似乎不能用作输出，只能单独以图像形式显示，不知道为什么。

下图为窗函数为256时的两个对比。可以看到右边图的频率分辨率相比左图有了较大提升。但是存在许多噪点。

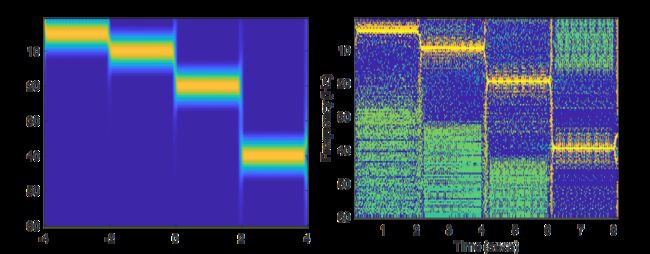
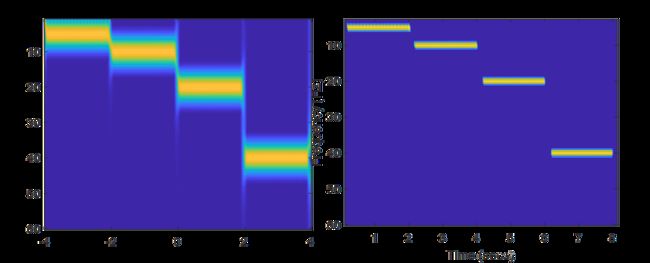
第二种是将小于某个数值的数归零，提高频率分辨率。
格式如下：
spectrogram(___,‘MinThreshold’,thresh)
参考第2节中的格式如下
spectrogram(z2,h,wlen-hop,f,fs,‘MinThreshold’,-14,‘yaxis’);
set(gca,‘YDir’,‘reverse’);
结果如下图所示

5 提取相位信号

短时傅里叶变换不仅可以提取信号的幅值，还可以提取信号的相位。
幅值的提取方法为abs，相位的提取方法为angle。

例：

clear

load mtlb;
z=mtlb;
L=length(z);
t=(1:L)/Fs;

z2=wextend(1,'sym',z,round(length(z)/2));
wlen=512;%设置窗长
hop=1;%平移步长
z2=wkeep1(z2,L+1*wlen);%中间截断


h=hamming(wlen);%设置海明窗的窗长
f=100:1:1000;
[tfr2,f,t2]=spectrogram(z2,h,wlen-hop,f,Fs,'reassigned','yaxis');
tfr2=tfr2*2/wlen*2;
figure
imagesc(t,f,angle(tfr2))%提取相位
colormap([linspace(0,1,32)'*ones(1,3);linspace(1,0,32)'*ones(1,3)])

信号的相位图如下：