机械臂运动学--欧拉角和四元数

1.Introduction

本文尝试从几何直观的角度理解欧拉角和四元数，主要参考3Blue1Grown的四元数系列视频。

2.欧拉角

根据wiki上对于欧拉角的介绍，根据旋转方式分为Proper Euler angle和Tait–Bryan angle，目前传感器使用最多的是yaw-pitch-roll（对应的旋转顺序是ZYX）。

根据对应的旋转顺序，可以根据XYZ对应的单位向量在原坐标系xyz上的投影上的投影反算欧拉角。

• 第一次旋转
  原x轴单位向量旋转到了$N^{\tau }$。
  
  $$sin(\psi )=x2/\sqrt{1-x_3^2}$$
• 第二次旋转
  绕着$y^{\tau }$将x‘旋转到了最终的位置X。
  $$sin(\theta )=x_3$$
• 第三次旋转
  将$y^{\tau }$旋转到了最终的位置Y，将z’旋转到了最终的位置Z，观察ZY平面。
  
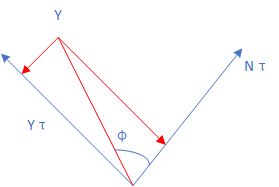
  在Y0Z平面内，满足
  $$sin(\varphi )=Y^{\tau }$$
  $$Y^{\tau }cos(\theta )=Y_3$$
  $$sin(\varphi )=Y_3/\sqrt{1-x_3^2}$$

3.frame transform 和 point transform

3.1 变换公式

3.1.1 变换关系

以二维线性变换为例（Rotate, transform and scale这三种变换属于线性变换）。

$(v1,v2)$可以看成是x,y轴单位向量经过坐标变换后的结果。
从column space的角度描述：
$$v1X^{\prime }+v2Y^{\prime }=P$$
用矩阵形式表示：
$$\left[\begin{array}{cc}v1& v2\end{array}\right]\left[\begin{array}{c}{X}^{\prime }\\ Y^{\prime }\end{array}\right]=\left[\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right]\text{\hspace{1em}(3.1)}$$
注意（X’, Y’）对应旋转后的坐标系上对应的坐标值，（x’, y’）基坐标系对应的坐标值。

3.1.2 记住公式

根据$v1$和$v2$对应旋转后坐标系中的坐标值（1，0）和（0，1）,可以简单的作图画出$v1$和$v2$,很容易求解出$v1$和$v2$。

3.2 坐标变换和点变换的关系

3.2.2 点变换

对点进行变换自然左乘一个变换矩阵。
$$M\left[\begin{array}{c}x\\ y\end{array}\right]=\left[\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right]$$

3.2.2 坐标变换

坐标变换，点在坐标系上的位置并没有发生变化，反求新坐标系上相对于新基底的坐标值，
根据公式3.1，已知（x’, y’）求（X’, Y’）。
求解的方法，通过矩阵求逆便可容易得出。

4.四元数

四元数部分按照3Blue1Brown的视频，进行叙述。
$重点:找到实轴，找到虚轴，实轴和虚轴组成平面，发生旋转$

4.1 四元数定义

根据线性代数内容，线性变换矩阵存在特征向量，在变换过程中，方向不发生改变，对应旋转矩阵，这个特征向量就是旋转轴。知道旋转轴和旋转角度，可以得到四元数。
$$cos(\frac{\alpha }{2})+sin(\frac{\alpha }{2})(xi+yj+zk)=w+ai+bj+ck\text{\hspace{1em}(4.1)}$$

4.1.1 旋转变换的四元数表达

将点p（三位空间中向量表示），进行旋转，旋转结果用四元数表示为：
$$f(p)=qp{q}^T\text{\hspace{1em}(4.2)}$$

4.1.2 两次旋转的相对旋转角

将点p第一次旋转成p’，再进行旋转一次成p’’,已知第一次旋转对应的四元数q0和最终状态对应的四元数q2，计算第二次相对于第一次的四元数q1以及相对旋转角θ。
$$q_1=q_2\ast q^T$$

4.1.3 questions

1.为什么点旋转是公式4.2的形式，qp有什么意义？
2.为什么四元数公式4.1中，使用$\frac{\alpha }{2}$,而不是$\alpha$
下面先用球极投影描述四元数相乘.

4.1.4 复向量乘积

图中的复向量$v（2,i）$将单位向量变换到了当前复向量的位置。

任意的一个向量w，和该向量的乘积$v\ast w$表示。

4.2球极投影

球极投影可以描述旋转效应，具有降维的效果，一维可以描述二维旋转，这样就可以用三位空间中的球极投影表示四元数。这也要求球极投影针对的向量的模为1。

4.2.1 二维空间

二维空间中单位圆上的点，可以用球极投影表示，球极投影的优点是降低了数据的维数（2维变成1维），四元数变换后的结果就可以在三维的球极投影上表示了。

4.2.2 三维空间

在三维空间中，此时虚轴用$(i,j)$线性组合而成。

从三位空间开始，球极投影开始变得复杂了，为了直观的表示球极投影的效果，重点关注实轴和球与虚平面的交线经过变换后的球极投影（即其在$(i,j)$上的投影）

4.2.3 四维空间

$(i,j,k)$对应的向量是作为球极投影映射的方向，实轴坐标在$[cos(-\pi /2),cos(\pi /2)]$在单位球的内部；
实轴对应$[cos(\pi /2),cos(-\pi /2)]$在单位球的外部。

实轴和三个虚轴的关系：实轴和三个虚轴全部垂直。

$（i,j,k）$线性组合成旋转轴，当$（i,j,k）$对应坐标全为0时，表示没有旋转。

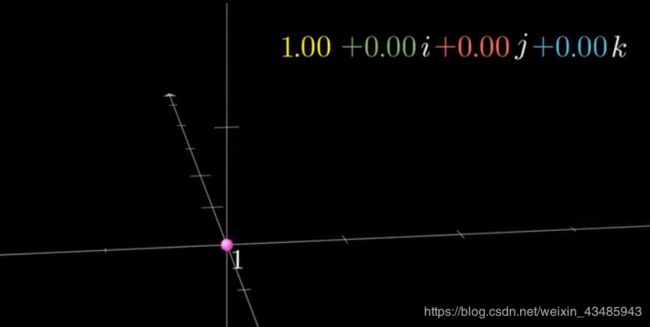
• 可视化三位空间中的球极投影
  对于四位空间的球极投影，通过
  1.单位向量$i,j,k和实轴$单位向量经过变换后的投影数值，
  2.如果绕j旋转，画出$ik$组成的圆环。
  3.$i,j,k$经过旋转变换后组成的超球。
  
• 旋转轴变换后的球极投影（对应着变换的模长）
  假设现在旋转轴是$j$,分析$f(j)$(这个很重要，我们希望四元数旋转过后并不改变向量的模长)
  再回到之前的一个图，
  如果绕j轴，右手旋转，越来越远，如上图。
  如果绕j轴，左手旋转，f(j)被转回来了。
  
  右手逆时针旋转$\theta$
  
  左手顺时针旋转$\theta$
  
  旋转用四元数相关的公式表示：
  $$f(p)=q_{1}p{q}_2$$
  当$q_2是q_1$的共轭时，此时沿着旋转轴旋转了两次，并且模长为1。这也就解释了4.1中的问题。

4.3 四元数变换

类比于矩阵变换，矩阵变换包含了旋转和放缩。

对于四元数而言，只有单位四元数才只包含旋转。$四元数乘法和dotproduct是两回事$

4.3.1 四元数乘法

4.3.2 四元数的逆

对于单位四元数，四元数的逆就是该四元数的共轭。
$$p^{-1}=p^T$$

5. References

1. https://eater.net/quaternions
2. https://en.wikipedia.org/wiki/Euler_angles
3. https://www.youtube.com/watch?v=d4EgbgTm0Bg