深度剖析ROC曲线以及AUC指标
首先,我们要知道,ROC描绘的是一条曲线,而AUC则是ROC曲线下的面积,是一个数值。
接下来,在正式讲解之前,我们先来看一个例子:
假设测试样本集的数量为1k个,其中A类样本有950个,B类样本有50个;共有2个分类器,C1和C2;
其中:
分类器C1划分的结果是将950个A类样本都判定为A类,即50个B类样本也判定为A类,即分类器C1将全部样本都预测为A类,则分类准确率为95%;
分类器C2划分的结果是将950个A类样本有正确预测了800个A类,剩余150个A类误判为B类,而50个B类样本正确预测了25个B类,剩余25个B类误判为A类,则分类器C2的准确率为(800+25)/1K*100%=82.5%.
从表面上来看,我们可以得出一个结论:
分类器C1的准确率比分类器C2的准确率要高
但是,直观来说,我们知道分类器C1只是单纯的将全部的样本都预测都A类,这种做法是非常不明智的。举个栗子给你听就知道,比如你可以把两个同学当做两个分类器,在某一场考试中(假设只有判断题),由于出题者出题不太规范,导致大部分判断题的答案都是正确的,这时候同学C1的策略就是每次都选择正确,所以导致了这场考试同学C1的成绩要比C2高。不过在除了这次失误考卷的情况下,其他考试卷对错选项都是非常均衡的,这时候我们可以明显的看出C2同学要远远比C1同学厉害的多!!!
So,in a word:
在实际情况中,我们不能够单独以单个评价指标去衡量我们分类器的好坏,特别是在样本分布非常不均匀的情况下。针对这种情况,有学者就引入了一种能够不随样本变化或者在样本分布不均匀的情况下都不会受影响的评价指标,也即是我们今天所要讲解的ROC和AUC指标,下面我们将对其进行讲解下。
注:下文内容参考自论文:‘An introduction to ROC analsis‘,作者为:Tom Fawcett
看不懂的可以跟着我的节奏来,我会在关键的地方加入注解帮助你更好的理解。
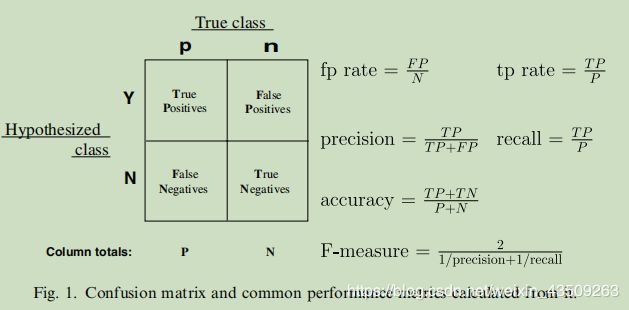
我们首先来看下图一:

其中,关于准确率、精确率、召回率、F-score的区别参考博文:点击进入
这里重点讲解下tp rate(TPR)和fp rate(FPR)
1- TPR(True Positive Rate)公式如下所示:
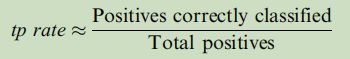
TPR作为ROC曲线的纵轴,有时候也称为召回率;其分子为所有被正确分类的正样本(positive),分母为所有正样本;即在所有的正样本中,有多少被你预测对了?
2- FPR(False Positive Rate)公式如下所示:
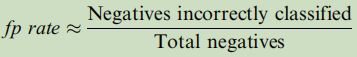
FPR作为ROC曲线的横轴,有时候也称为错误预警率;其分子为所有被预测错误的负样本(negative),分母为总的负样本;即在所有的负样本中,有多少被你预测错了。
接着再引入几个概念:
3- sensitivity,即灵敏度,它等同于recall,即召回率;
4- specificity,即特异度,它等同于 1 - FPR,公式如下:

这里分母等价于Total negative,因此在初始所有负样本中,可能有一部分被正确分类成负样本(True negative),还有一部分负样本被误判为正样本(False positive),即假的正样本。
ps:这里可能会有点绕, 大家先理清楚下上面一些基础的概念再接着往下看,否则看完还是会一头雾水,一口吃不成胖子,不用着急,知识点是需要一点一点消化掉的。
理顺的话,让我们接下往下看 - - - - - - - - >
ROC图描述了收益(真阳性,纵轴)和成本(假阳性,横轴)之间的相对权衡。
观察上图,我们结合医学诊断方面的具体例子先来分析下一些特殊点:
1- 对于对角线上的点,比如点(0, 0), (1, 1)以及点C点,它们的预测都是靠随机猜测的;
2- 对于左上方的点(0, 1)来说,这个是我们追求的终极目标,简而言之,他就是一个神医!因为他把有病的病人都给全部诊断出来了,而健康的人都确认过眼神,是没病的人。不过在实际中,几乎是不可能存在这么完美的分类器的~~所以上述五个点中,D点所示的性能是最棒的!
3- 对于右下方的点(1, 0)来说,它简直就是最糟糕的结果,简而言之,他就是一个彻底的庸医!因为他把健康的人都诊断为病人,而把病人都确诊为健康的人…
到这里我们应该明确下,一个离散分类器在ROC空间中只产生一个点(一个离散分类器产生一个混淆矩阵,一个混淆矩阵计算出一个点);此外,对于一些其他的分类器,如生成模型的naive bayes即朴素贝叶斯分类器来或者神经网络来说,它们预测的结果是一个概率,而我们现在得到的是一个分数score,在这种情况下,我们默认分数越高,则说明概率就越高。调整不同的阈值threshold,我们便可以得到不同的点,最后再通过将这些点连接起来,我们便可以得到一条ROC曲线。接下来我们来具体描述下如何绘制ROC曲线。
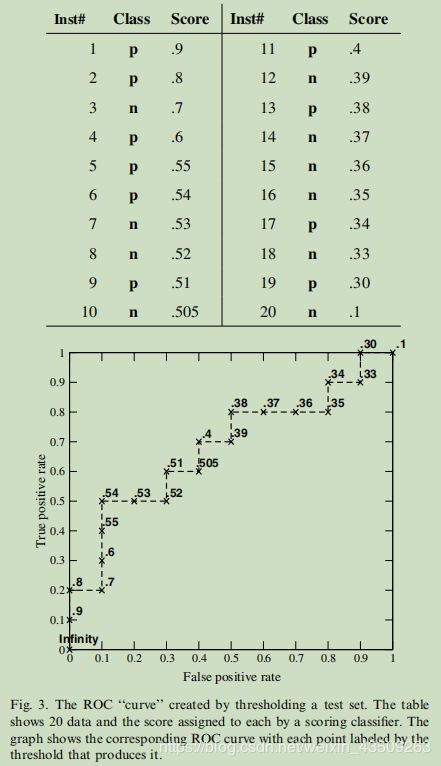
图3展示了一个具有20个样本点的测试样本集所对应的ROC曲线。由有限个实例集生成的ROC曲线实际上是一个阶跃函数,当实例数趋近于无穷时,阶跃函数趋近于真实曲线。图3中的阶跃函数取自一个非常小的实例集,这是为了方便我们理解每个点的推导。在图3中实例我们按它们的得分进行排序,ROC图中的每一个点都用产生它的分数阈值标记。阈值为+∞时产生点(0,0)。当我们将阈值降低到0.9时,第一个阳性实例被分类为阳性,产生(0,0.1)。随着阈值进一步降低,曲线向上并向右攀升,最终到达(1,1),阈值为0.1。
ps:这些点我再解释下怎么看,先看表格中的分类,如果是正类(对应class=p),则向上前进0.1,如果是负类(对应class=n),则向左前进0.1。
虽然测试集很小,但是我们可以对分类器做一些尝试性的观察。它似乎在图中更保守(对应图中的左边)的区域表现得更好;ROC点(0.1, 0.5)的准确率最高(70%)。这就相当于说分类器在识别可能的正面(预判正确)比识别可能的负面(预判错误)更擅长。<这句话的意思是这个分类器做出正确判断的几率比做出错误判断的几率要大,这是我们所要的分类器>还请注意,分类器的最佳准确度出现在P=0.54的阈值上,而不是我们所期望的分布均衡时的P=0.5。<这里解释下,就是说一般我们在预测输出时,拿二分类来说吧, 我们的预判函数时会将阈值设置为0.5,即大于等于0.5的都归为正类,小于0.5的归为负类>下面我们来解释下这种情况。
ROC图的一个重要特点是,它衡量的是分类器产生良好的相对实例分数的能力。分类器不需要产生精确的、校准过的概率估计;它只需要产生相对准确的分数,用来区分正类和负类的情况。
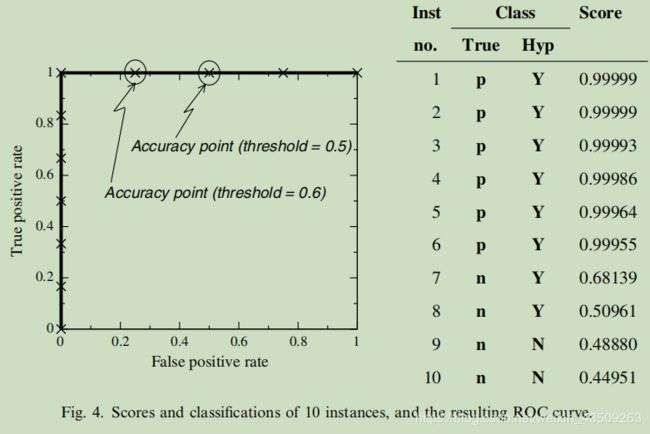
考虑图4所示的简单实例得分,它来自一个朴素贝叶斯分类器。将预测的类(if score> 0.5, Y, else N)与真实的类进行比较,我们可以看到分类器得到的实例7和8是错误的,所以准确率为80%。但是,请考虑图左侧的ROC曲线。曲线从(0,0)垂直上升到(0,1),然后水平行进到(1,1),这说明该测试集的分类性能很好,为什么会出现这种差异?
这归根于每个人衡量的标准不同。我们可以看到,上图中圈出来的两个点,如果我们设定0.5的阈值,那么我们可以得出图4中右边的那个点,它的准确率是80%;前面我们分析到,越靠近左上方的位置,分类器的性能就越好,可以看到,如果我们将阈值设定为0.6,可以得到左边的那个点,它的分类准确率达到90%。<这里解释下,看上面那个表格,就是score值大于0.6的我们就将它归为Y类,否则归为N类,这样结果就只有第7个实例预测错误,所以有9个实例预测正确了>
ROC曲线有一个吸引人的特性:
它对样本分布的变化不敏感。如果一个测试集中的正、负样本的比例发生变化,ROC曲线不会发生变化。要了解为什么会这样,请考虑图1中的混淆矩阵。注意,类分布—正实例与负实例的比例—是左(+)列与右(-)列之间的关系。任何使用来自这两列的值的性能度量都对类倾斜天生敏感。准确率、精确率、召回率和F分数等指标使用来自混淆矩阵的两列的值。随着类分布的变化,这些度量也会发生变化,即使基本的分类器性能根本没有变化。ROC图是基于tp率和fp率,所以它并不依赖于类的分布。
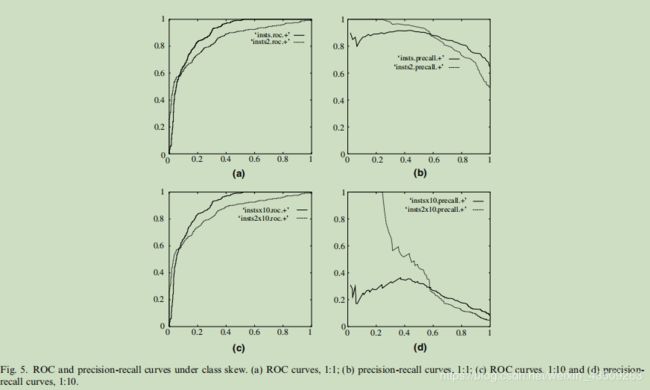
研究人员发现,如上图所示,(a) (b)两图显示的是在样本均衡的情况下,我们使用ROC曲线(对应a图)和精确率-召回率曲线(对应b图)都能够很好的判断出分类器的性能。而当我们尝试将负样本的实例增加10倍时(还是用同一个分类器),我们可以明显的观察到,ROC曲线完全不受变化(对应c图),而精确率-召回率曲线(对应d图)则发生了敏感性的变化。
到这里差不多了,我们现在来总结下:
(1)AUC(Area Under Carve)描述的是ROC(Receiver Operating Characteristic,接受者操作特性曲线)曲线下的面积,其值介于0到1之间,它的本质意思是指预测正确的可能性比预测错误的可能性要大多少;
ps:这句话是个人观点,我是这么理解的,比如我们考虑极端点(0, 1),这个点所对应的分类器堪称完美分类器,因为它把所有有病的都检测出来,所有没病的都诊断为健康了,此时对应的AUC为1。
(2)ROC曲线不受样本分布变化的影响,而精确率、召回率、F-socre等会对样本分布具有很大的敏感性;