AI-语音处理理论和应用-GMM
学习目标
• 了解语音处理的基础知识及应用
• 掌握语音处理的基本步骤
• 掌握语音处理的主要技术
• 了解语音处理的难点与展望
传统语音模型
GMM
混合模型
• 混合模型是一个可以用来表示在总体分布中的含有K个子分部的概率模型,换句话说搞混合模型表示了观测数据在总体中的概率分布,它是一个由K个子分部组成的混合分布。例如:由几个高斯分布混合起来的模型叫高斯混合模型,几个线性模型混合在一起的模型叫线性混合模型。
• 混合模型是一个统计模型,包含固定效应和随机效应两种效应的混合。在统计学中,混合模型是代表一个大群体中存在子群体的概率模型;混合模型不要求观测数据提供关于子分布的信息来计算观测数据在总体分布中的概率。
混合模型的定义
• 混合模型定义:
y ( i , t ) = α + X ( i , t ) β + ε ( i , t ) . y(i,t) = \alpha + X(i,t)\beta + \varepsilon (i,t). y(i,t)=α+X(i,t)β+ε(i,t). (i=1,2,3,…,N;t=1,2,3,…,T)
• 参数解释:
• y(i,t)为回归变量(标量);
• α为截距,β为k1阶回归变量列向量(包括k个回归量);
• X(i,t)为k1阶回归系数列向量(包括k个回归量);
• ε(i,t)为误差项(标量);
• 在不同的混合方法中,具体的公式要根据实际应用确定
概率论基础知识
随机变量
• 随机变量:表示随机试验各种结果的实值单值函数。例如某一时间内公共汽车站等车乘客人数。
• 按照随机变量可能取得的值,可以把它们分为两种基本类型:
• 离散型随机变量:即在一定区间内变量取值为有限个或可数个。例如某地区某年人口的出生数、死亡数,某药治疗某病病人的有效数、无效数等。
• 连续型随机变量:即在一定区间内变量取值有无限个,或数值无法一一列举出来。例如某地区男性健康成人的身长值、体重值,一批传染性肝炎患者的血清转氨酶测定值等。
概率密度函数
• 连续型随机变量的概率密度函数是一个描述这个随机变量的 • F x ( x ) = ∫ − ∞ x f x ( t ) d t F_{x}(x)=\int_{-\infty }^{x}f_{x}(t)dt Fx(x)=∫−∞xfx(t)dt
• 概率密度函数性质:
• f(x)≥0;在任意点的取值大于等于0
• ∫ -∞到+∞f(x)dx=1;随机变量所有可能取值情况之和等于1
• P(a,b)= ∫a到bf(x)dx;在某个区间内的取值概率等于在区间内的概率密度函数的积分
高斯分布
• 高斯分布,又名正太分布,最早由棣莫弗在求二项分布的渐近公式中得到。高斯在研究测量误差时从另一个角度导出了它,是一个在数学、物理及工程等领域都非常重要的概率分布,在统计学的许多方面有着重大的影响力。
• 若随机变量X服从一个数学期望为μ,方差为σ2的正态分布,记为N(μ,σ2)。其概率密度函数为正态分布的期望值μ决定了其位置,其标准差σ决定了分布的幅度。当μ=0,σ=1时的正太分布是标准正太分布。公式如下:
f ( x ) = 1 2 π σ e − ( x − μ ) 2 2 σ 2 f(x)=\frac{1}{\sqrt{2\pi \sigma }}e^{-\frac{(x-\mu )^{2}}{2\sigma ^{2}}} f(x)=2πσ1e−2σ2(x−μ)2
高斯分布曲线

• 正态曲线呈钟型,两头低,中间高,左右对称因其曲线呈钟形。
• 标准差越大,曲线越扁平;反之,标准差越小,曲线越瘦高。
单高斯模型
• 当样本数据x是一维数据时,高斯分布村从下方概率密度函数:
P ( x ∣ θ ) = 1 2 π σ 2 e − ( x − μ ) 2 2 σ 2 P(x\mid \theta)=\frac{1}{\sqrt{2\pi \sigma ^{2}}}e^{-\frac{\left ( x-\mu \right )^{2}}{2\sigma ^{2}}} P(x∣θ)=2πσ21e−2σ2(x−μ)2
(其中μ为数据均值,σ为数据标准差)
•当样本数据X是多维数据,高斯分布遵从下方概率密度函数:
P ( x ∣ θ ) = 1 ( 2 π ) D x e − ( x − μ ) T ∑ ( x − μ ) − 1 2 P(x\mid \theta)=\frac{1}{(2\pi )^{\frac{D}{x}}}e^{-\frac{\left ( x-\mu \right )^{T}\sum (x-\mu )^{-1}}{2}} P(x∣θ)=(2π)xD1e−2(x−μ)T∑(x−μ)−1
(其中μ为数据均值,∑为协方差,D为数据维度。)
最大似然法
• 最大似然法(Maximum Likelihood,ML)也叫极大似然估计,是一种具有理论性的点估计法。最大似然估计是一种统计方法,它用来求一个样本集的相关概率密度函数的参数。
• 此方法的基本思想是:当从模型总体随机抽取n组样本观测值后,最合理的参数估计量应该使得从模型中抽取该n组样本观测值的概率最大,而不是像最小二乘估计法旨正在得到使得模型能最好地拟合样本数据的参数估计量。
• 公式
• 假设有N个独立数据点,均服从某种分布Pr(x;θ),我们想找到一组参数θ,使得生成这些数据点的概率最大,这个概率就是:
∏ i = 1 N P r ( x i ; θ ) \prod_{i=1}^{N}Pr(x_{i};\theta) i=1∏NPr(xi;θ)
• 称为似然函数(Likelihood Function)。通常单个点的概率很小,连乘之后数据会更小,容易造成浮点数下溢,所以一般取其对数,变成:
∑ i = 1 N l o g P r ( x i ; θ ) \sum_{i=1}^{N}logPr(x_{i};\theta) i=1∑NlogPr(xi;θ)
• 称为log-likelihood function。接下来就可以进行求导,然后哦求得使得上面式子值最大的参数 θ。我们认为去的这些观察值的可能性是很小的,但是参数θ却使得这一切以最大可能性的发生了。
概率与似然
• 概率和似然,两者概念类似,但又很不相同。加入随机变量X服从高斯分布,概率是指在给定参数(均值,方差)的条件下,X=x的可能性;而似然则指X=x的条件下,某一组参数的真实性大小。
• 概率:是给定某一参数值,求某一结果的可能性。
• 例如:抛一枚匀质硬币10次,6次正面向上的可能性多大?“匀质硬币”,表明参数值是0.5,“抛10次,六次正面向上”这是一个结果,概率是求这一结果的可能性。
• 似然:是给定某一结果,求某一参数值的可能性。
• 例如:抛一枚硬币10次,结果是6次正面向上,其是匀质的可能性多大?
• “抛10次,结果是6次正面向上”,这是一个给定的结果,问“匀质”的可能性,即求参数值=0.5的可能性
单高斯模型参数学习
• 对于单高斯模型,我们可以用最大似然法估算参数θ的值,θ=argmaxθL(θ),这里我们假设了每个数据点都是独立的,似然函数由概率密度函数给出:
L ( θ ) = ∏ j = 1 N P ( x j ∣ θ ) L(\theta )=\prod_{j=1}^{N}P(x_{j}\mid \theta) L(θ)=j=1∏NP(xj∣θ)
• (由于每个点发生的概率都很小,乘积会变得极其小,不利于计算和观察,因此通常我们用 Maximum Log-Likelihood 来计算。)
• 因为 Log 函数具备单调性,不会改变极值的位置,同时在 0-1 之间输入值很小的变化可以引起输出值相对较大的变动:
l o g L ( θ ) = ∑ j = 1 N l o g P ( x j ∣ θ ) logL\left ( \theta \right )=\sum_{j=1}^{N}logP(x_{j}\mid \theta ) logL(θ)=j=1∑NlogP(xj∣θ)
利用最大似然估计求解
• 概率密度函数:通过观测数据得到
• 似然函数:通过一系列样本得到
• 对数似然函数:简化计算
• 求导且令方程为零
• 解方程
高斯混合模型
• 单高斯模型不能很好解决具体遇到的问题
• GMM是单一高斯概率密度函数的延伸,GMM能够平滑地近似任意形状的密度分布。高斯混合模型种类有单高斯模型(Single Gaussian Model, SGM)和高斯混合模型(Gaussian Mixture Model, GMM)两类。
• 类似于聚类,根据高斯概率密度函数(Probability Density Function, PDF)参数不同,每一个高斯模型可以看作一种类别,输入一个样本x,即可通过PDF计算其值,然后通过一个阈值来判断该样本是否属于高斯模型。很明显,SGM适合于仅有两类别问题的划分,而GMM由于具有多个模型,划分更为精细,适用于多类别的划分,可以应用于复杂对象建模。
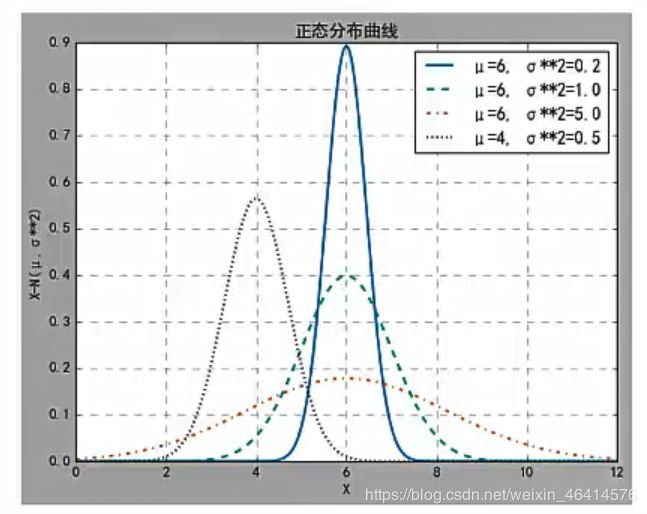
• 高斯混合模型的概率分布:
P ( x ∣ θ ) = ∑ k = 1 K α k ϕ ( x ∣ θ k ) P\left ( x\mid \theta \right )=\sum_{k=1}^{K}\alpha _{k}\phi (x\mid \theta _{k}) P(x∣θ)=k=1∑Kαkϕ(x∣θk)
• 对于这个模型而言,参数θ=(μk,σk,αk)也就是每个子模型的期望、方差(或协方差)、在混合模型中发生的概率。
• 参数解释:
• xj表示第j个观测数据,j=1,2,3,…,N;K是混合模型中高斯模型的数量;αk是观测数据属于第k个子模型的概率,αk≥0,∑k=1到K ak=1;Φ(x|θk)是第k个子模型的高斯分布密度函数,θk = (μk,σ^2 k);
• 对于高斯混合模型,Log-Likelihood 函数是:
l o g L ( θ ) = ∑ j = 1 N l o g P ( x j ∣ θ ) = ∑ j = 1 N l o g ( ∑ k = 1 N α k ϕ ( x ∣ θ k ) ) logL\left ( \theta \right )=\sum_{j=1}^{N}logP\left ( x_{j}\mid \theta \right )=\sum_{j=1}^{N}log\left ( \sum_{k=1}^{N}\alpha _{k} \phi \left ( x\mid \theta _{k} \right )\right ) logL(θ)=j=1∑NlogP(xj∣θ)=j=1∑Nlog(k=1∑Nαkϕ(x∣θk))
• 如何计算高斯混合模型的参数呢?
• 这里我们无法像单高斯模型那样使用最大似然法来求导求得使 likelihood 最大的参数,因为对于每个观测数据点来说,事先并不知道它是属于哪个子分布的(Hidden Variable),因此 log 里面还有求和,K个高斯模型的和不是一个高斯模型,对于每个子模型都有未知的αk,μk,σk,直接求导无法计算。需要通过迭代的方法求解。
EM算法
• 最大期望算法(Expectation Maximization Algorithm),是一种迭代算法,用于含有隐变量(Hidden Variable)的概率参数模型的最大似然估计或极大后验概率估计。
• EM 算法是 Dempster,Laind,Rubin 于 1977 年提出的求极大似然估计参数的一种方法,它可以从非完整数据集中对参数进行 MLE 估计,是一种非常简单实用的学习算法。这种方法可以广泛地应用于处理缺损你数据,截尾数据,带有噪声等所谓的不完全数据。

EM算法求解
• 初始化参数:
• E步骤:依据当前参数计算每个数据j来自于子模型k的可能性:
γ j k = α k ϕ ( x j ∣ θ k ) ∑ k = 1 K α k ϕ ( x j ∣ θ k ) \gamma _{jk}=\frac{\alpha _{k} \phi\left ( x_{j}\mid \theta _{k} \right ) }{\sum_{k=1}^{K}\alpha _{k}\phi\left ( x_{j}\mid \theta _{k} \right ) } γjk=∑k=1Kαkϕ(xj∣θk)αkϕ(xj∣θk)
• 其中,j=1,2,3…,N;k=1,2,3,…,K
• M步骤:计算新一轮迭代的模型参数:
μ k = ∑ j N ( γ j k x j ) ∑ j N γ j k , k = 1 , 2 , 3 , . . . , N \mu _{k}=\frac{\sum_{j}^{N}\left ( \gamma jk^{x}j \right )}{\sum_{j}^{N}\gamma jk},k=1,2,3,...,N μk=∑jNγjk∑jN(γjkxj),k=1,2,3,...,N
∑ k = ∑ j N γ j k ( x j − μ k ) ( x j − μ k ) T ∑ j N γ j k \sum k=\frac{\sum_{j}^{N} \gamma jk\left ( x_{j}-\mu _{k} \right )\left (x_{j}-\mu _{k} \right )^{T} }{\sum_{j}^{N}\gamma jk} ∑k=∑jNγjk∑jNγjk(xj−μk)(xj−μk)T
α k = ∑ j = 1 N γ j k N \alpha_{k}=\frac{\sum_{j=1}^{N}\gamma _{jk}}{N} αk=N∑j=1Nγjk
• 其中K=1,2,3,…,N
• 迭代:重复计算 E-step 和 M-step 直至收敛
EM具体迭代步骤
• 初始化参数
• E步骤:求期望
• M步骤:求极大,计算新一轮迭代的模型参数
• 迭代至收敛
GMM计算步骤
• 高斯混合模型函数
• 概率密度函数
• 似然函数
• 对数似然函数
• EM算法求解
GMM优缺点
• 优点:
• 拟合能力强
• 对语音特征匹配概率最大化
•缺点:
• 无法处理序列因素
• 无法处理线性或近似线性数据