对偶四元数——使用python3实现对偶四元数的符号运算 v2.0

实现对偶四元数简单的符号运算，数值运算，2.0版本

改正了v1.0中的一些错误，添加了四元数归一化，转换为齐次变换矩阵，转换为螺旋，转换为双矢量，三种共轭等功能

可以先看最后例子的效果

---

目录

1 创建一个包含对偶算子的单项式类

2 创建多项式类

3 创建对偶四元数类

4 举个例子

---

1 创建一个包含对偶算子的单项式类

主要功能：单项式乘法，输出

monomial.py

# coding: utf-8
"""
@ Time: Created on 2019.04.07\n
@ Author: yukino\n
@ Description：Create a monomial class
"""


class Monomial:
    def __init__(self, coef=0, para={}, dual=False):
        self.coef = coef  # 系数
        self.var = para.keys()  # 元
        self.deg = para.values()  # 次数
        self.para = para  # 变量
        self.dual = dual  # 对偶符

    def __mul__(self, monomial):
        """乘法运算符重载"""
        if self.dual and monomial.dual is True:  # 判断是否都是对偶数
            return None  # 如果都是返回空
        else:
            result = Monomial()
            result.coef = self.coef
            result.para = self.para.copy()
            result.coef *= monomial.coef
            for k, v in monomial.para.items():
                if k in result.para.keys():  # 如果元存在则次数相加
                    result.para[k] += v
                else:
                    result.para[k] = v  # 否则在字典中添加新键值对
            result.dual = self.dual or monomial.dual  # 计算对偶符
            return result

    def multiply(self, monomial):
        result = Monomial()
        result.coef = self.coef
        result.para = self.para.copy()
        result.coef *= monomial.coef
        for k, v in monomial.para.items():
            if k in result.para.keys():
                result.para[k] += v
            else:
                result.para[k] = v
        return result

    def __str__(self):
        """输出重载"""
        self.para = dict(sorted(self.para.items(), key=lambda x: x[0]))
        term = ""
        coef = approx(self.coef)
        if self.para == {}:  # 如果只有系数
            if self.dual:
                return '@(' + str(coef) + ')'
            else:
                return str(coef)  # 只返回系数
        else:
            for key in self.para:
                if self.para[key] == 1:  # 如果次数为1则不打印幂
                    term += " " + (str(key))
                else:
                    term += " " + (str(key)) + "^" + str(self.para[key])
            if coef == 1.0:  # 如果系数为1则不打印系数
                if self.dual is True:
                    return "@(" + term.strip() + ")"
                else:
                    return term.strip()
            elif coef == -1.0:  # 如果系数为-1则只打印符号
                if self.dual is True:
                    return "@(-" + term.strip() + ")"
                else:
                    return "-" + term.strip()
            else:
                if self.dual is True:
                    return "@(" + str(coef) + term.strip() + ")"
                else:
                    return str(coef) + term.strip()


def approx(num):
    e = 1e-15
    num1 = round(num, 1)
    if abs(num - num1) < e:
        return num1
    else:
        return round(num, 4)
    


if __name__ == '__main__':
    # test
    a = Monomial(3, {'x': 2, 'y': 3, 'z': 4})
    b = Monomial(-3, {'a': 5, 'y': 6, 'z': 7})
    c = Monomial(9)
    d = b * a
    print(d)

2 创建多项式类

主要功能：多项式加法，减法，乘法，输出，化简等

polynomial.py

# coding: utf-8
"""
@ Time: Created on 2019.03.13\n
@ Author: yukino\n
@ Description：Create a polynomial class
"""
from monomial import Monomial


class Polynomial:
    """
    多项式类
    初始化参数：任意数量Monomial类
    """
    def __init__(self, *monomial):
        self.monomials = monomial  # 单项式组成的元组
        self.coefs = [i.coef for i in monomial]  # 单项式系数

    def __str__(self):
        """输出重载"""
        term = []
        if self.monomials.__len__() == 1:  # 如果只有一个单项式则不打印括号
            term.append(str(self.monomials[0]))
        else:
            for monomial in self.monomials:
                if monomial not in [None]:  # 如果单项式不为空
                    if monomial.coef < 0:  # 系数小于0则加括号
                        term.append("(" + str(monomial) + ")")
                    elif monomial.coef > 0:
                        term.append(str(monomial))
        term = ' + '.join(term)
        return term

    def __add__(self, polynomial):
        """加法运算符重载"""
        return Polynomial(*(self.monomials + polynomial.monomials))

    def __sub__(self, polynomial):
        """减法运算符重载"""
        minus = []
        for monomial in polynomial.monomials:
            temp = Monomial()
            temp.coef = -monomial.coef
            temp.para = monomial.para.copy()
            temp.dual = monomial.dual
            minus.append(temp)
        return Polynomial(* (self.monomials + tuple(minus)))

    def __mul__(self, polynomial):
        """乘法运算符重载"""
        mult = []
        for monomialP in polynomial.monomials:
            for monomialR in self.monomials:
                mult.append(monomialR * monomialP)
        return Polynomial(* mult)


def simplify(poly):
    """
    多项式化简函数\n
    Input: Polynomial Class\n
    Output: Polynomial Class
    """
    # 分离实部与对偶部
    real = []
    dual = []
    for monomial in poly.monomials:
        if monomial.dual is True:
            dual.append(monomial)
        else:
            real.append(monomial)
    # 简化实部
    resparas = []
    rescoefs = []
    monomials = []
    paras = [monomial.para for monomial in real]
    coefs = [monomial.coef for monomial in real]
    for i in range(len(paras)):
        if not paras[i] in resparas:
            resparas.append(paras[i])
            rescoefs.append(coefs[i])
        else:
            rescoefs[resparas.index(paras[i])] += coefs[i]
    for i in range(len(rescoefs)):
        monomials.append(Monomial(rescoefs[i], resparas[i]))
    # 简化对偶部
    resparas = []
    rescoefs = []
    paras = [monomial.para for monomial in dual]
    coefs = [monomial.coef for monomial in dual]
    for i in range(len(paras)):
        if not paras[i] in resparas:
            resparas.append(paras[i])
            rescoefs.append(coefs[i])
        else:
            rescoefs[resparas.index(paras[i])] += coefs[i]
    for i in range(len(rescoefs)):
        monomials.append(Monomial(rescoefs[i], resparas[i], True))
    simp = Polynomial(*monomials)
    return simp


if __name__ == '__main__':
    # test
    a = Monomial(3, {'x': 2, 'y': 3, 'z': 4}, True)
    b = Monomial(-3, {'a': 5, 'y': 6, 'z': 7})
    c = Polynomial(a, b)
    A = Polynomial(a)
    B = Polynomial(b)
    C = A + A
    D = simplify(C)
    print(A)
    print(B)
    print(C)
    print(D)

3 创建对偶四元数类

dualquaternion.py

# coding: utf-8
"""
@ Time: Created on 2019.04.07\n
@ Author: yukino\n
@ Description：Create a dual-quaternion class
"""
from polynomial import Polynomial, simplify
from monomial import Monomial
from math import atan2, sqrt, sin, tan
from numpy import pi


class DualQuaternion:
    """
    对偶四元数类\n
    初始化参数：List[8 个 Ploynomial 类]
    """

    def __init__(self, quaterlist):
        """构造函数, 1个由8个多项式类构成的列表"""
        self.real = quaterlist[:4]  # 实部
        self.dual = quaterlist[4:]  # 对偶部
        self.all = quaterlist  # 所有参数
        self.coefs = [i.coefs[0] for i in quaterlist]  # 所有系数, 用于数值计算

    def __str__(self):
        """输出重载"""
        q = ['', 'i', 'j', 'k']
        result = []
        for i in range(4):
            # 如果只有系数0则不输出
            if len(set(self.real[i].coefs)) == 1 and self.real[i].coefs[0] == 0:
                pass
            else:
                result.append('(' + str(self.real[i]) + ')' + q[i])
        for i in range(4):
            if len(set(self.dual[i].coefs)) == 1 and self.dual[i].coefs[0] == 0:
                pass
            else:
                result.append('(' + str(self.dual[i]) + ')' + q[i])
        term = ' + '.join(result)
        return term

    def __add__(self, dualquater):
        """对偶四元数加法重载"""
        result = []
        self = self.all
        dualquater = dualquater.all
        for i in range(8):
            result.append(self[i] + dualquater[i])
        return DualQuaternion(result)

    def __sub__(self, dualquater):
        """对偶四元数减法重载"""
        result = []
        self = self.all
        dualquater = dualquater.all
        for i in range(8):
            result.append(self[i] - dualquater[i])
        return DualQuaternion(result)

    def __mul__(self, dualquater):
        """对偶四元数乘法重载"""
        q = self.all
        p = dualquater.all
        x0 = q[0]*p[0] - q[1]*p[1] - q[2]*p[2] - q[3]*p[3]
        x1 = q[0]*p[1] + q[1]*p[0] + q[2]*p[3] - q[3]*p[2]
        x2 = q[0]*p[2] - q[1]*p[3] + q[2]*p[0] + q[3]*p[1]
        x3 = q[0]*p[3] + q[1]*p[2] - q[2]*p[1] + q[3]*p[0]
        y0 = q[0]*p[4] - q[1]*p[5] - q[2]*p[6] - q[3]*p[7] + \
            q[4]*p[0] - q[5]*p[1] - q[6]*p[2] - q[7]*p[3]
        y1 = q[0]*p[5] + q[1]*p[4] + q[2]*p[7] - q[3]*p[6] + \
            q[4]*p[1] + q[5]*p[0] + q[6]*p[3] - q[7]*p[2]
        y2 = q[0]*p[6] - q[1]*p[7] + q[2]*p[4] + q[3]*p[5] + \
            q[4]*p[2] - q[5]*p[3] + q[6]*p[0] + q[7]*p[1]
        y3 = q[0]*p[7] + q[1]*p[6] - q[2]*p[5] + q[3]*p[4] + \
            q[4]*p[3] + q[5]*p[2] - q[6]*p[1] + q[7]*p[0]
        return DualQuaternion([x0, x1, x2, x3, y0, y1, y2, y3])

    def printArray(self):
        """
        打印对偶四元数每项\n
        Output: List[str]
        """
        q = ['s:', 'i:', 'j:', 'k:', '@s:', '@i:', '@j:', '@k:']
        for i in range(8):
            print(q[i] + '\t\t' + str(self.all[i]))

    def dualqsimp(self):
        """
        对偶四元数类简化函数\n
        Output: Polynomial Class
        """
        result = []
        for i in self.all:
            result.append(simplify(i))
        return DualQuaternion(result)


    def originalconj(self):
        """
        第一种共轭运算, 是四元数共轭的延伸，记作q'\n
        q = a + @b ,q' = a' + @b'\n
        a' = s - oi - mj - nk\n
        q*q'是标量
        """
        result = self.deepcopy()
        for poly in result.real[1:4]:
            for mo in poly.monomials:
                mo.coef = -mo.coef
        for poly in result.dual[1:4]:
            for mo in poly.monomials:
                mo.coef = -mo.coef
        return result

    def dualconj(self):
        """
        第二种共轭运算, 只是变换了对偶部的符号, 记作q^\n
        q = a + @b ,q^ = a - @b
        """
        result = self.deepcopy()
        for poly in result.dual[0:4]:
            for mo in poly.monomials:
                mo.coef = -mo.coef
        return result

    def conj(self):
        """
        第三种共轭运算, 是前两种的结合, 记作q'^\n
        q = a + @b, q^' = a' - @b'\n
        用于计算坐标转换:\n
        Output = q * Input * q'^
        """
        result = self.deepcopy()
        for poly in result.real[1:4]:
            for mo in poly.monomials:
                mo.coef = -mo.coef
        for mo in result.dual[0].monomials:
            mo.coef = -mo.coef
        return result

    def normpow(self):
        """
        输出对偶四元数模的平方, q = a + @b\n
        |q|^2 = q*q' =  a*a' + @(a*b' + b*a')\n
        单位对偶四元数是指模为1\n
        即: a*a' = 1, a*b' + b*a' = 0
        """
        return self * self.originalconj()

    def inverse(self):
        """
        TODO: 逆运算
        """
        pass

    def toVector(self):
        """
        转化为平移矢量和xyz欧拉角
        """
        r = self.coefs[:4]
        d = self.coefs[4:]
        c = sqrt(r[0]**2+r[1]**2+r[2]**2+r[3]**2)
        if c != 0:
            r = [i/c for i in r]
        p = [2*(r[0]*d[1]-r[1]*d[0]+r[2]*d[3]-r[3]*d[2]),
             2*(r[0]*d[2]-r[1]*d[3]-r[2]*d[0]+r[3]*d[1]),
             2*(r[0]*d[3]+r[1]*d[2]-r[2]*d[1]-r[3]*d[0])]
        z = atan2(2*r[1]*r[2]-2*r[0]*r[3], r[0]**2+r[1]**2-r[2]**2-r[3]**2)
        y = atan2(-2*(r[0]*r[2]+r[1]*r[3]), 1)
        x = atan2(2*(r[2]*r[3]-r[0]*r[1]), r[0]**2-r[1]**2-r[2]**2+r[3]**2)
        zpi = round(z/pi, 2)
        ypi = round(y/pi, 2)
        xpi = round(x/pi, 2)
        print('\nEuler(pi): ', approx([xpi, ypi, zpi]), 'Vector: ', approx(p))
        return [[x, y, z], p]

    def toScrew(self):
        """
        转化为螺旋, 输出:[s,sr,d,theta,rd,h,t]\n
        s:原部 sr:对偶部\n
        theta:绕螺旋轴转角 d:沿螺旋轴位移\n
        rd:直线矩, 原点到螺旋轴的垂线 h:螺距
        t: 平移
        """
        r = self.coefs[:4]
        d = self.coefs[4:]
        c = sqrt(r[0]**2+r[1]**2+r[2]**2+r[3]**2)
        if c != 0:
            r = [i/c for i in r]
        theta = 2*atan2(sqrt(r[1]**2+r[2]**2+r[3]**2), r[0])
        s = [i/sin(theta/2) for i in r[1:]]
        t = [2*(r[0]*d[1]-r[1]*d[0]+r[2]*d[3]-r[3]*d[2]),
             2*(r[0]*d[2]-r[1]*d[3]-r[2]*d[0]+r[3]*d[1]),
             2*(r[0]*d[3]+r[1]*d[2]-r[2]*d[1]-r[3]*d[0])]
        de = s[0]*t[0] + s[1]*t[1] + s[2]*t[2]
        cot = tan(pi/2-theta/2)
        rd = [(t[0] - de*s[0] + cot*(t[1]*s[2]-t[2]*s[1]))/2,
              (t[1] - de*s[1] + cot*(t[2]*s[0]-t[0]*s[2]))/2,
              (t[2] - de*s[2] + cot*(t[0]*s[1]-t[1]*s[0]))/2]
        h = 2*pi*de/theta
        sr = [(rd[1]*s[2]-rd[2]*s[1])+h*s[0],
              (rd[2]*s[0]-rd[0]*s[2])+h*s[1],
              (rd[0]*s[1]-rd[1]*s[0])+h*s[2]]
        screw = [s, sr, de, theta, rd, h, t]
        print('\nScrew:\n\t(s, sr): (', approx(s), approx(sr), ')')
        print('\ttheta(pi): ', approx2(theta/pi), '\td: ', approx2(de))
        print('\tr: ', approx(rd), '\th: ', approx2(h))
        print('\tt: ', approx(t))
        return screw

    def toTranMatrix(self):
        """
        转化为旋转矩阵和位移,只适合数值运算\n
        输出该对偶四元数变换后的坐标系，是坐标系变换\n
        Output:[x轴坐标, y轴坐标, z轴坐标, o点坐标]
        """
        r = self.coefs[:4]
        d = self.coefs[4:]
        c = sqrt(r[0]**2+r[1]**2+r[2]**2+r[3]**2)
        if c != 0:
            r = [i/c for i in r]
        p = [2*(r[0]*d[1]-r[1]*d[0]+r[2]*d[3]-r[3]*d[2]),
             2*(r[0]*d[2]-r[1]*d[3]-r[2]*d[0]+r[3]*d[1]),
             2*(r[0]*d[3]+r[1]*d[2]-r[2]*d[1]-r[3]*d[0])]
        R1 = [r[0]*r[0]+r[1]*r[1]-r[2]*r[2]-r[3]*r[3],
              2*(r[1]*r[2]+r[0]*r[3]),
              2*(r[1]*r[3]-r[0]*r[2])]
        R2 = [2*(r[1]*r[2]-r[0]*r[3]),
              r[0]*r[0]-r[1]*r[1]+r[2]*r[2]-r[3]*r[3],
              2*(r[2]*r[3]+r[0]*r[1])]
        R3 = [2*(r[1]*r[3]+r[0]*r[2]),
              2*(r[2]*r[3]-r[0]*r[1]),
              r[0]*r[0]-r[1]*r[1]-r[2]*r[2]+r[3]*r[3]]
        print('\nRationMatrix:')
        r1 = [round(i, 2) for i in R1]
        r2 = [round(i, 2) for i in R2]
        r3 = [round(i, 2) for i in R3]
        rp = [round(i, 2) for i in p]
        print("|{:6} {:6} {:6}|".format(r1[0], r2[0], r3[0]))
        print("|{:6} {:6} {:6}|".format(r1[1], r2[1], r3[1]))
        print("|{:6} {:6} {:6}|".format(r1[2], r2[2], r3[2]))
        # print('\t|', r1[0], '\t', r2[0], '\t', r3[0], '\t|')
        # print('\t|', r1[1], '\t', r2[1], '\t', r3[1], '\t|')
        # print('\t|', r1[2], '\t', r2[2], '\t', r3[2], '\t|')
        print('Translation:')
        print('\t', rp)
        return [R1, R2, R3, p]

    def toMatrix(self):
        """
        将对偶四元数转换为4x4齐次变换,只适合数值运算\n
        q = a + @b\n
        a = w + oi + mj + nk 表示旋转\n
        b = 0 + x/2 + y/2 + z/2 表示位移x, y, z\n
        Output:R = [x轴坐标, y轴坐标, z轴坐标, o点坐标]\n
        相当于 p2 = q * p1 * q'^ \n
        p2 = R[:4] * p1 + R[4]\n
        """
        d = self.coefs[4:]
        r = self.coefs[:4]
        c = sqrt(r[0]**2+r[1]**2+r[2]**2+r[3]**2)
        if c != 0:
            r = [i/c for i in r]
        p = [d[1], d[2], d[3]]
        R1 = [r[0]*r[0]+r[1]*r[1]-r[2]*r[2]-r[3]*r[3],
              2*(r[1]*r[2]+r[0]*r[3]),
              2*(r[1]*r[3]-r[0]*r[2])]
        R2 = [2*(r[1]*r[2]-r[0]*r[3]),
              r[0]*r[0]-r[1]*r[1]+r[2]*r[2]-r[3]*r[3],
              2*(r[2]*r[3]+r[0]*r[1])]
        R3 = [2*(r[1]*r[3]+r[0]*r[2]),
              2*(r[2]*r[3]-r[0]*r[1]),
              r[0]*r[0]-r[1]*r[1]-r[2]*r[2]+r[3]*r[3]]
        return [R1, R2, R3, p]

    def normalize(self):
        """
        实部归一化
        """
        result = self.deepcopy()
        rl = result.real
        r = result.coefs[:4]
        c = r[0]**2 + r[1]**2 + r[2]**2 + r[3]**2
        c = sqrt(c)
        for i in rl:
            i.monomials[0].coef = i.monomials[0].coef/c
        return result


def symbol(sym, dual=False):
    """
    符号定义函数，定义为多项式类\n
    Input: str\n
    Output: Polynomial Class
    """
    return Polynomial(Monomial(1, {sym: 1}, dual))


def number(num, dual=False):
    """
    数字定义函数，定义为多项式类\n
    Input: int or float\n
    Output: Polynomial Class
    """
    return Polynomial(Monomial(num, dual=dual))


def symbols(*syms):
    """一次定义多个符号的函数，方便定义符号，由于使用全局变量，应谨慎使用"""
    names = globals()
    for sym in syms:
        if sym[0] == '@':
            names[sym[1:]] = Polynomial(Monomial(1, {sym[1:]: 1}, True))
        else:
            names[sym] = Polynomial(Monomial(1, {sym: 1}))


def quaterSym(*syms):
    """
    生成对偶四元数类所需的列表参数\n
    Input: 8 str, int or float\n
    Output: List of Polynomial Class
    """
    result = []
    for i in range(4):
        if isinstance(syms[i], str):
            result.append(symbol(syms[i]))
        else:
            result.append(number(syms[i]))
    for i in range(4, 8):
        if isinstance(syms[i], str):
            result.append(symbol(syms[i], True))
        else:
            result.append(number(syms[i], True))
    return result


def approx(nums):
    e = 1e-15
    r = []
    for num in nums:
        num1 = round(num, 1)
        if abs(num - num1) < e:
            r.append(num1)
        else:
            r.append(round(num, 4))
    return r


def approx2(num):
    e = 1e-15
    num1 = round(num, 1)
    if abs(num - num1) < e:
        return num1
    else:
        return round(num, 4)


if __name__ == '__main__':
    a = [2.0000000000000004, 0.9999999999999998, 1.717456, 3.1415, 2.5000000000000004]
    b = approx(a)
    print(b)

4 举个例子

需要安装mpl_toolkits库

plot3d.py  写了一些方便绘图的函数

# coding: utf-8
"""
@ Time: Created on 2019.04.7\n
@ Author: yukino\n
@ Description：Some function for drawing 3d plot
"""
import numpy as np
import math
from math import sin, cos, asin, sqrt
import matplotlib.pyplot as plt
import mpl_toolkits.mplot3d as p3d


def coord(plot, xyz=[[1, 0, 0], [0, 1, 0], [0, 0, 1]], o=[0, 0, 0], orgin='O', long=1):
    """绘制坐标系
    输入窗口plot，x，y，z轴坐标, o原点坐标, 坐标轴长度"""
    # ax.quiver(x, y, z, u, v, w, length=0.1, normalize=True)
    plot.text(o[0], o[1], o[2], orgin, color='black')
    plot.quiver(o[0], o[1], o[2], xyz[0][0], xyz[0][1], xyz[0][2], color='r', length=long,
                arrow_length_ratio=0.1, normalize=True)
    plot.quiver(o[0], o[1], o[2], xyz[1][0], xyz[1][1], xyz[1][2], color='g', length=long,
                arrow_length_ratio=0.1, normalize=True)
    plot.quiver(o[0], o[1], o[2], xyz[2][0], xyz[2][1], xyz[2][2], color='b', length=long,
                arrow_length_ratio=0.1, normalize=True)


def screw(plot, s, p, h):
    """绘制螺旋线
    输入窗口名称plot, 螺旋轴s, 螺旋轴位置p, 螺距h,"""
    b = asin(-s[2])
    a = asin(round(s[1]/cos(b), 8))
    theta = np.linspace(-4 * np.pi, 4 * np.pi, 100)
    r = sqrt(p[0]**2 + p[1]**2 + p[2]**2)
    x = np.linspace(-2*h, 2*h, 100)
    y = r * np.sin(theta)
    z = r * np.cos(theta)

    
    R1 = [s[0], -sin(a), cos(a)*sin(b)]
    R2 = [s[1], cos(a), sin(a)*sin(b)]
    R3 = [s[2], 0, cos(b)]
    R = np.array([R1, R2, R3])
    xyz = np.matmul(R, np.vstack((x, y, z)))
    x = np.add(xyz[0, :], p[0])
    y = np.add(xyz[1, :], p[1])
    z = np.add(xyz[2, :], p[2])

    plot.plot(x, y, z)


def SetAxLim(plot, lim=5):
    plot.set_xlim(-lim, lim)
    plot.set_ylim(-lim, lim)
    plot.set_zlim(-lim, lim)


def myquiver(plot, start=[0, 0, 0], end=[1, 1, 1], color='b', name='v'):
    end1 = tuple(approx(end))
    end = [j-i for i, j in zip(start, end)]
    sd0 = (end[0])**2
    sd1 = (end[1])**2
    sd2 = (end[2])**2
    length = sqrt(sd0 + sd1 + sd2)
    plot.quiver(start[0], start[1], start[2], end[0],
                end[1], end[2], color=color, length=length,
                arrow_length_ratio=0.1, normalize=True)
    name = name + str(end1)
    plot.text(end1[0], end1[1], end1[2], name, color='black')


def approx(nums):
    e = 1e-15
    r = []
    for num in nums:
        num1 = round(num, 1)
        if abs(num - num1) < e:
            r.append(num1)
        else:
            r.append(round(num, 4))
    return r



def EanglesToRmatrix(theta):
    """ZYX欧拉角转旋转矩阵"""
    R_x = np.array([[1, 0, 0],
                    [0, math.cos(theta[0]), -math.sin(theta[0])],
                    [0, math.sin(theta[0]), math.cos(theta[0])]
                    ])
    R_y = np.array([[math.cos(theta[1]), 0, math.sin(theta[1])],
                    [0, 1, 0],
                    [-math.sin(theta[1]), 0, math.cos(theta[1])]
                    ])
    R_z = np.array([[math.cos(theta[2]), -math.sin(theta[2]), 0],
                    [math.sin(theta[2]), math.cos(theta[2]), 0],
                    [0, 0, 1]
                    ])
    R = np.dot(R_z, np.dot(R_y, R_x))
    return R


if __name__ == '__main__':
    fig = plt.figure(figsize=(8, 8))
    # ax = fig.gca(projection='3d')
    ax = p3d.Axes3D(fig)
    x = [1, 0, 0]
    y = [0, 1, 0]
    z = [0, 0, 1]
    theta = [np.pi/4, 0, np.pi/4]
    R = EanglesToRmatrix(theta)
    x1 = np.dot(R, x)
    y1 = np.dot(R, y)
    z1 = np.dot(R, z)

    coord(ax, x, y, z)
    coord(ax, x1, y1, z1, [0.5, 0.5, 0.5])
    ax.set_xlim(-1, 1)
    ax.set_ylim(-1, 1)
    ax.set_zlim(-1, 1)
    # 比例一致
    ax.get_proj = lambda: np.dot(p3d.Axes3D.get_proj(ax), np.diag([1, 1, 1, 1]))
    plt.show()

主测试程序：

# coding: utf-8
"""
@ Time: Created on 2019.04.07\n
@ Author: yukino\n
@ Description：For debugging programs
"""
import dualquaternion as dq
import plot3d
import numpy as np
import math
import matplotlib.pyplot as plt
import mpl_toolkits.mplot3d as p3d

# 创建对偶四元数参数，可以是符号也可以是数字
o1 = dq.quaterSym(1, 0, 0, 0, 0, 0, 0, 0)
t = dq.quaterSym(1, 0, 0, 0, 0, 1, 1, 1)
r = dq.quaterSym(1, 1, 1, 0, 0, 0, 0, 0)
v = dq.quaterSym(1, 0, 0, 0, 0, 1, 1, 1)

q1 = dq.DualQuaternion(o1)
qr = dq.DualQuaternion(r).normalize()
print(qr)
qt = dq.DualQuaternion(t)
qv = dq.DualQuaternion(v)
print('qt\': \t', qt.conj())
vr = (qr * qv * qr.conj()).dualqsimp()

vt = (qt * qv * qt.conj()).dualqsimp()
print('vt: \t', vt)

tr = (qt*qr).dualqsimp()
print('tr: \t', tr)
# print((qr.conj()*qt.conj()).dualqsimp())
vrt = (tr * qv * tr.conj()).dualqsimp().dualqsimp()
print('input: \t', qv)
print('output: ', vrt)

O1 = q1.toMatrix()
A = qv.toMatrix()
B = vr.toMatrix()
C = vrt.toMatrix()
D = tr.toTranMatrix()
E = tr.toVector()
S = tr.toScrew()
fig = plt.figure(figsize=(8, 8))
ax = p3d.Axes3D(fig)
# plot3d.coord(ax, A[:3], A[3], 'O1')
# plot3d.coord(ax, B[:3], B[3], 'O2')
# plot3d.coord(ax, C[:3], C[3], 'O3')
ax.quiver(S[4][0], S[4][1], S[4][2], S[0][0], S[0][1], S[0][2], color='black', length=10,
                arrow_length_ratio=0.02, normalize=True, pivot='middle')
plot3d.screw(ax, S[0], S[4], S[5])
plot3d.coord(ax, D[:3], D[3], 'O4')
plot3d.coord(ax, O1[:3], O1[3])
plot3d.myquiver(ax, end=A[3], color='r', name='v1')
plot3d.myquiver(ax, end=C[3], color='g', name='v2')
plot3d.myquiver(ax, end=S[4], color='black', name='r')
# plot3d.myquiver(ax, end=[A[3][0], -A[3][1], -A[3][2]], color='r', name='v3')
plot3d.myquiver(ax, D[3], C[3], 'b', name='v4')
# ax.quiver(0, 0, 0, A[3][0], A[3][1], A[3][2], color='r', length=3,
#                 arrow_length_ratio=0.1, normalize=True)
# ax.quiver(0, 0, 0, C[3][0], C[3][1], C[3][2], color='b', length=3,
#                 arrow_length_ratio=0.1, normalize=True)
# ax.quiver(D[3][0], D[3][1], D[3][2], C[3][0], C[3][1], C[3][2], color='g', length=3,
#                 arrow_length_ratio=0.1, normalize=True)

plot3d.SetAxLim(ax, 3)
plt.show()

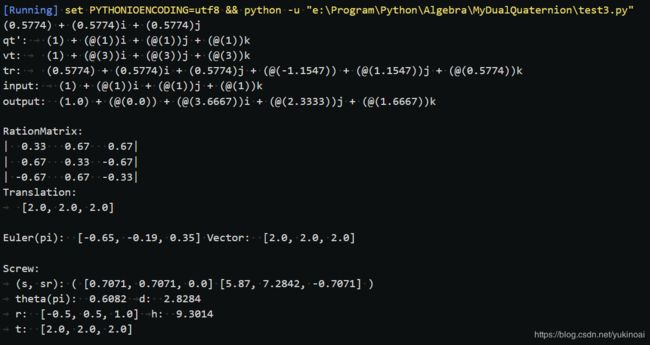
结果如下，输出转换后的结果，齐次变换矩阵，欧拉角与平移矢量，以及螺旋表示参数

同时输出转换后的矢量与坐标系及螺旋轴的图：