浅谈整除分块
浅谈整除分块
前言
我们在学习整除分块之前,首先你得整除分块就是是个什么,它跟分块(区间操作)相似但是不同(我学的时候有点小懵一直以为是分块然后额)。
我是在学习莫比乌斯反演的时候看到要先学前置知识整除分块,于是去学习。(整除分块比狄利克雷卷积简单多了,虽然我到现在还是不会狄利克雷卷积和莫比乌斯反演。)
例题
洛谷
余数求和
给出正整数n和k,计算G(n, k)=k mod 1 + k mod 2 + k mod 3 + … + k mod n的值,其中k mod i表示k除以i的余数。例如G(10, 5)=5 mod 1 + 5 mod 2 + 5 mod 3 + 5 mod 4 + 5 mod 5 …… + 5 mod 10=0+1+2+1+0+5+5+5+5+5=29
推导题意可得
∑ i = 1 n k m o d i \sum_{i=1}^{n} {k\mod i} ∑i=1nkmodi
首先数据之大让你没有办法去暴力,所以它的难度是提高+省选-,那么再次推导,可得式子为
= ∑ i = 1 n k − i ∗ ( k / i ) =\sum_{i=1}^{n}{k-i*(k/i)} =∑i=1nk−i∗(k/i)
= n ∗ k − ∑ i = 1 n i ∗ ( k / i ) =n*k-\sum_{i=1}^{n}{i*(k/i)} =n∗k−∑i=1ni∗(k/i)
到此为止,就是整除分块的模板了,即求 ∑ i = 1 n i ∗ ( k / i ) \sum_{i=1}^{n}{i*(k/i)} ∑i=1ni∗(k/i),当然 k / i k/i k/i向下取整
到此,离开本题去讲整除分块的模板
整除分块
∑ i = 1 n n / i \sum_{i=1}^{n}{n/i} ∑i=1nn/i
以下为模板
#include这组数据是怎么的出来了的呢?
推导过程
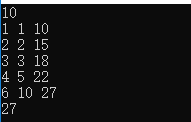
当 n = 10 n=10 n=10时,我们手动求 ∑ i = 1 n n / i \sum_{i=1}^{n}{n/i} ∑i=1nn/i
![]()
可知答案是27,与上面相同,那么这是为什么?
整除分块,是把 n n n除以每一个 i i i的商相同的分成一块
由10的样例可知
重复的商相同的部分,我们可以在O(1)的时间内求出来
枚举 ( l , r ) (l,r) (l,r)
( l , r ) (l,r) (l,r)区间即对于该区间任何一个数来说, n n n \ i = n i=n i=n \ l l l
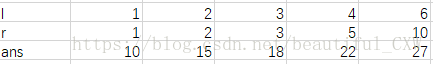
我们从1开始枚举 l l l,
r = n / ( n / l ) r=n/(n/l) r=n/(n/l)
然后 l = r + 1 l=r+1 l=r+1
这样可以把该序列整除分块了
然后整除分块的时间即从O( r − l + 1 r-l+1 r−l+1)缩减到了O(1)
回到例题
我们在把 = n ∗ k − ∑ i = 1 n i ∗ ( k / i ) =n*k-\sum_{i=1}^{n}{i*(k/i)} =n∗k−∑i=1ni∗(k/i)推导一下
可以得到对于每个区间 ( l , r ) (l,r) (l,r)来说,公式为 ( k / l ) ∗ ( r − l + 1 ) ∗ ( l + r ) / 2 (k/l)*(r-l+1)*(l+r)/2 (k/l)∗(r−l+1)∗(l+r)/2(自己推一推,很快滴)
即可得到答案
#include