DeepFace: Closing the Gap to Human-Level Performance in Face Verification
原文地址
摘要
在现代人脸识别技术中,检测->对齐->表示->分类是其常规流程的四个阶段。为了运用分段仿射变换并且从九层深度神经网络中导出人脸表示,我们通过使用精确的3D人脸模型重温了人脸对齐和人脸表示的步骤。这个深度网络相较于标准卷积层,涵盖了超过1.2亿个不共享权重而使用一些局部连接层的参数。因此我们在迄今为止最大的人脸集(属于4000个身份并带有标签的四百万张人脸图片集)中训练这个网络。在无限制环境的情况下,学习过的人脸表示将基于模型的精确的人脸对齐与大型人脸数据库相结合,对人脸进行了效果显著的概括(即使只使用一个简单的分类器,也能得到很好的效果)。基于LFW人脸数据库,我们的方法得到了97.35%的准确率,相较于目前最先进的人脸验证技术,我们减少了超过27%的错误,非常接近人类的表现。
1. 介绍
在无限制的图像内进行的人脸识别技术位于算法感知革命的最前线。人脸识别技术在社会和文化方面可能产生的影响是远远不能想象的,目前在这个领域中,机器与人类视觉系统之间的表现差距,可以作为在不得不处理这些影响之前的一个缓冲。
我们呈现了一个系统(DeepFace),其可在无限制人脸识别中,基于大多数主流的基准,减少了非常大一部分还需要处理的差距。并且,它现在已经到达了人类级别准确率的边缘。这个系统是在一个庞大的人脸数据集(相较于以前构造评估基准的人脸集,该数据集中的人脸是从差异性更大的人口中获得的)中训练的并且它的性能已经优于现在存在的只有非常小的适应性的系统。此外,该系统提供一种极其紧凑的人脸表示,与成千上万近期其他系统的表面特征转换全然不同。
所提出的系统与该领域中的大多数贡献不同,它使用了深度学习(DL)框架代替了精心构造的特征。伴随着近期在各种领域(视觉、演说和语言模型)获得的成功,深度学习对于处理大型训练数据集来说是非常合适的。尤其对于人脸,学习过的网络以一种鲁棒的方式获取人脸外观的成功高度依赖于快速3D对齐的步骤。网络结构是基于对齐已完成、每个人脸区域在像素级别被固定的设想构造的。因此该网络结构才有可能不需要像许多其他网络一样,应用一些卷积层来完成这部分工作,直接从未处理过的像素的RGB值中进行学习。
总的来说,我们做出了以下贡献:
a. 高效深度神经网络结构的发展和为了获得对其他数据集也可以很好的归纳的人脸表示而对有标签的大型人脸集产生影响的学习方法。
b. 一个高效的基于3D人脸模型的人脸对齐系统。
c. 在LFW数据集与YTF数据集中显著推进了技术状态,几乎达到了人类的表现水平,减少了超过50%的错误率。
1.1 相关工作
大数据和深度学习 近几年来,大量照片被搜索引擎检索并且上传到社交网络上,这其中包括多种无限制的材料,例如物体、人脸和场景。
大数据量和计算资源的增加已经使更强大的统计模型的使用变得可行。这些模型极大地增强了视觉系统对于一些重要变化(例如非刚性变形、聚类、遮挡和光照以及位于计算机视觉应用领域核心的所有问题)的鲁棒性。常规机器学习方法(例如支持向量机、主成分分析和线性判别分析)限制了对大数据量产生影响的能力,深度神经网络展示了更好的缩放属性。
近期出现了一股对神经网络的兴趣浪潮。尤其是大型深度网络一度展现出令人印象深刻的结果:他们(深度神经网络)被运用到大型训练数据。并且可扩展的计算资源(例如成千上万的CPU和GPU内核)变得可以得到。最为显著的是,Krizhevsky以及其他人展示了通过标准反向传播训练得到的大型深度卷积网络在训练大型数据集时可以达到优异的识别准确率。
最先进的人脸识别 在过去的二十年里,当在被控制在一致的环境下(约束)拍摄的静止图像中识别正面人脸时,人脸识别错误率已经被减少了超过三个数量级。许多供应商为了边境管制和智能生物识别的应用部署了复杂精细的系统。然而,这些系统对因素(例如光照、表情、遮挡和年龄等)的变化十分敏感,这使他们在这样一种无限制的设定下对人脸识别的表现大幅度退化。
大多数现今的人脸识别方法都使用了手工标定特征点的方法。此外,即使是在最早的LFW稿件中,这些特征常常被结合以加强表现。目前引领表现的系统特许使用成千上万的图片描述符。相反的,我们的方法是直接应用于像素的RGB值,产生十分紧凑同时又稀疏的描述符。
深度神经网络过去也应用于人脸探测、人脸对齐和人脸验证当中。在无限制的领域,Huang等人将深度神经网络用作输入LBP特征值并且展示了深度神经网络与传统方法结合时产生的改进。在我们的方法中,我们使用未处理的图像作为我们的底层表示,并且为了突出我们工作的贡献,我们避免我们的特征与构造好的描述符相结合。我们也提供了一种新的架构,其将通过结合3D对齐、为对齐后的输入定制架构、通过几乎两种数量级缩放神经网络和网络在非常大型的带标签的数据集里训练之后演示一种简单的知识传授方法来进一步推动在使用这些网络的情况下什么是能够达到的极限。
矩阵学习方法在人脸验证中被大量使用,经常与特定任务目标相结合。目前,使用大量带标签的人脸数据集最成功的系统运用了一种聪明转换技术,其采用了联合贝叶斯模型在LFW图像域内含有2995个不同主体的99773张图片的数据集上进行学习。为了展示特征的有效性,我们保留了学习琐碎步骤的距离。
2. 人脸对齐
尽管对齐被广泛使用,现今对于无限制的人脸识别仍然没有完整的物理矫正方法。3D模型在近几年来已经变得不受欢迎了,尤其是在无限制的环境中。然而,既然人脸是3D物体,只要正确执行,我们认为(3D模型)是正确的方法。在这篇论文中,我们描述了一个包含基于基准点可分析3D人脸模型的系统,该系统被用作扭曲一个探测到的人脸片段成为一个正面的3D模型(frontalization)。
与近期的很多对齐文献相似的是,我们的对齐方法是基于使用基准点探测器来引导对齐过程的,我们使用了一个相对来说简单的基准点探测器,但是将其运用到一些迭代过程中使其输入被较好的矫正。在每一次迭代中,基准点被一个从图像描述符中得到训练来预测点布局支持向量回归器(SVR)所提取。我们的图像描述符基于LBP直方图(LBP Histograms),但是其他的特征也可以被考虑到。通过使用导出的相似矩阵来将图像转换为一张新的图像,我们可以在一个新的特征空间再一次运行基准点探测器进而矫正定位。
2D 对齐 我们以检测裁剪框内的6个基准点:双眼的中心点、鼻尖、嘴的坐标点(如插图1的(a)中所示)。六个点( j=1…6 )通过匹配 Ti2d:=(si,Ri,ti) (此时 xjanchor:=si[Ri|ti]∗xjsource )并且在新的变形后的图像上迭代至没有大型变换,最终形成2D相似变换: T2d:=T12d∗...∗Tk2d ,将图像近似缩放、旋转和转换成为六个固定定位。这种聚集变换生成一个如图1(b)中所示的2D对齐裁剪框。这种对齐方法与LFW-中一种常用语提升识别效率的方法相似。然而,相似变换无法补偿在无限制条件下尤其重要的平面外的旋转。
3D对齐 为了在非平面旋转的情况下对齐人脸,我们使用一个通用的3D形状模型和一个用于将2D对齐步骤中裁剪出来的图像弯曲成3D模型形状的3D仿射相机。这将生成一个3D对齐过后的裁剪图版本(如图1(g)中所示)。这是由使用二级支持向量回归器(SVR)定位在2D裁剪图中的额外的67个基准点x2d(如图1(c)中所示)形成的。我们简单的将USF Human-Id数据集中的3D扫描取平均值得到3D通用形状模型,其被后处理来表示对齐后的顶点 vi=(xi,yi,zi)ni=1 。我们手工在3D形状上添加67个固定点,并且以这种方式得到了67个检测到的点与它们参照的完整相似度。接着一个3D到2D的仿射相机P通过使用已知协方差 ∑ 和规范化的最小平方解决方法到线性系统 x2d=x3dP⃗ 上被固定,也就是说, P⃗ 最小化下述损失: loss(p⃗ )=rT∑−1r ,此时 r=(x2d−X3dP⃗ ) 是残余向量并且 X3d 是一个通过追踪 2×8 的矩阵 [xT3d(i),1,0⃗ ;0⃗ ,xT3d(i),1] (对于每个参考基准点 x3d(i) 而言, 0⃗ 代表的是一个由四个0组成的行向量)得到的 (67∗2)×8 矩阵。尺寸大小为 2×4 的仿射相机由8个未知向量 P⃗ 来表示。损失可在对协方差 ∑ 使用Cholesky分解的情况下被最小化,该方法可将问题转化为普通的最小方差问题。打个比方,因为在人脸轮廓上探测到的点所预估计的定位被相对于相机角度的视差严重影响,有许多噪声,我们则使用一个由基准点错误的估计方差所给出的 (67∗2)×(67∗2) 的协方差矩阵 ∑ 。
Frontalization 因为完整透视投影和非刚醒的变形没有被建模,固定好的相机P只是一个近似物。为了减少对于最后扭曲变形如此重要的身份关系因素的败坏,我们增加了每个参考基准点 x3d 对应的残余在r到x-y分量上,将其表示为
x˜3d 。这样一种张弛对于将2D图像以相对于人脸身份而言较小的变形目的而言是很合理的。如果不这样的话,失去重要的判别因素,人脸会在三维状态下被扭曲成相同的形状。最后,frontalization以这种根据67个基准点引出的德劳内三角剖分算法(Delaunay triangulation)从 x2d (source)到 x˜3d (target)的分段仿射T所实现。同时,关于相机P看不见的三角形,可以通过使用图片中混合它们的相对应的对称部分来完成替代。
3. 表示
近几年来,计算机视觉文献已经吸引了很多致力于描述符构造方面的研究。当这些描述符被应用到人脸识别中,大多都在人脸图像中对所有位置使用同一算子。随着近期越来越多的数据变得可以获得,因为可以为了特定的当前目标而发现和优化特征,基于学习的方法开始显示出在构造特征方面的优势。这里,我们通过一个大型深度网络来学习一个人脸图像的通用描述。
深度神经网络架构(DNN Architecture)和训练 我们在一个多类别的人脸识别任务重训练我们的深度神经网络,即给人脸图像进行身份的分类。 总体架构展示在图2中。一个3D对齐过的 152×152 像素大小的三通道(RGB)人脸图像被作为有32个滤波器大小为 11×11×3 卷积层C1的输入。由此产生的32个特征映射将被反馈到一个分别将每一个通道在 3×3 空间邻域上以 2 为大小的步幅取最大值的最大池化层M2(max-pooling)。随后是另一个大小为 9×9×16 有16个滤波器的卷积层C3。这三层是为了提取低级别的特征,类似简单的边缘和结构。最大池化层使卷积网络的输出对局部转换而言具有更强的鲁棒性。当运用到对齐过的人脸图片时,它们使网络对于小的配准错误也有更强的鲁棒性。然而,若干级的池化可能会导致网络失去具体面部构造和微结构精确位置信息。因此,我们只在第一个卷积层中运用最大池化。我们将这些初级层解释为一个前端自适应预处理阶段。尽管它们对大部分计算负责,它们持有非常少的参数。这些层仅仅将输入扩展为一组简单的局部特征。
后续的层(L4、L5和L6)不是局部连接的(比如一个被运用一个滤波器组的卷积层),而是在特征映射中的每一个位置都从不同组滤波器 这种进行学习。因为一个对齐后的图像的不同区有不同的局部统计量,卷积的空间平稳假设是不成立的。打个比方,眼睛和眉毛之间的区域与鼻子和嘴之间的区域相比较,展现出非常不同的外观并且具有更高的辨别能力。换句话说,我们通过利用我们的输入图像已经对齐过的这个事实定制深度神经网络(DNN)架构。局部层的使用并不影响特征提取的计算负担,但是对目标训练的参数数量会产生影响。只因我们有大型标记的数据集,我们可以负担三个大型局部连接层。局部连接层(不分享权重)的使用也可以被每一个局部连接层的输出单元会被输入图像的较大的patch所影响这一事实所证明是正确的。例如,L6的输出被输入的一个 74×74×3 的patch所影响,并且对齐过的人脸上如此大的patch之间几乎没有任何统计共享。
最后,最高两层(F7和F8)被全连接:每一个输出单元都被连接至所有的输入上。这些层能够捕获从人脸不同区域之间采集到的特征的相互关系,比如说眼睛和嘴巴的位置和形状。在神经网络中,第一个全连接层(L7)的输出在论文中将一直会被作为未处理的人脸表示特征向量来使用。至于表示,是和现有文献提出的基于LBP的表示方法(由直方图计算得到的普遍非常集中的描述子并且将其作为分类器的输入)相反的。
最后一个连接层的输出被反馈到一个在类标签中产生分布的 K−way softmax分类器(此时 K 为类的数量)。如果我们通过 ok 在一个给定的输入上表示网络的第 k 级输出, 那么被指定到第 k 类的概率则为softmax函数的输出: pk=exp(ok)/∑hexp(oh) 。
训练的目标是最大化准确类(人脸身份)的概率。我们通过最小化每个训练样本的交叉熵损失达到这个目标。如果k是一个给定输入的真实标签索引,那么损失则为: L=−logpk 。该损失(相对于上述参数)通过计算 L 的梯度和使用随机梯度下降法(SGD)更新参数值来实现最小化。梯度通过错误的反向传播来计算。上述网络产生的一个有趣的特征性质是它们都非常分散。平均地,在最高层,75%的特征含量准确而言,值为0。这主要是由于使用了ReLU激活函数: max(0,x) 。软阈值的非线性被运用到每一次卷积当中(局部连接层和全连接层,但是除了最后一层),使整个级联产生了强烈非线性和稀疏的特征。在使用正则化方法(也称做dropout,即在训练时将散乱的特征分量设定为0值)的时候,也会出现稀疏性。我们只在第一个全连接层使用上述正则化方法。大型的训练集使我们免于在训练中观察到显著的过拟合现象。
一张给定的图像 I ,其表示 G(I) 可以通过使用所述前馈网络计算出来。任何有 L 层的前馈神经网络都可以被看作是函数 glϕ 的组成。在我们的情况下,该表示为: G(I)=gF7ϕ(gL6ϕ(...gC1ϕ(T(I,θT))...)) 。该网络的参数值如第二部分所述,为: ϕ={C1,...,F7} 、 θ={x2d,P⃗ ,r⃗ } 。
标准化 作为最后一个阶段,为了减少对光照变化的敏感性,我们要将特征在0到1之间进行标准化:每一个特征向量的分量被其在训练集中的最大值所划分。随后进行 L2−normalization 操作: f(I):=G¯(I)/||G¯(I)||2 ,此时 G¯(I)i=G(I)i/max(Gi,ϵ) 。因为我们使用了ReLU激活函数,我们的系统对图像再缩放会导致图像密度的变化。倘若在深度神经网络中没有偏差,我们将可以达到完美的同变性。
4. 验证矩阵(Verification Metric)
随着监督方法相对于无监督的方法显现出明显的优势,验证两个输入实例是否属于同一个类(身份)在无限制人脸识别领域已经被广泛研究。通过训练目标域的训练集,(监督方法)能够通过对特征向量(或分类器)进行微调来更好地实现对数据集的特定分配。例如,LFW数据集中有大概75%的男性,大多是被专业摄像师拍摄的名人。正如[5]所证明的,在不同域分配的情况下训练和测试不仅会对结果产生显著的影响,而且为了得到更好的泛化和表现,还要求对人脸表示(或分类器)进行更进一步的微调。然而,调整一个模型以适应一个相对较小的数据集会减少其对于其他数据集的通用性。在本次工作中,我们致力于学习一个对若干数据集都能通用的无监督矩阵。我们的无监督相似性是简单存在与成果内部两个标准化的特征向量之间的。我们也在监督矩阵( χ2similarity 和Siamese网络)中进行了实验。
4.1 加权的卡方距离(Weighted χ2 distance)
在我们的方法中,标准化的DeepFace特征向量与基于直方图的特征向量具有若干相似性,比方说LBP:(1)包含非负值。(2)非常稀疏,(3)其值区间为 [0,1] 。因此,与LBP相似地,我们使用加权的卡方相似性方法: χ2(f1,f2)=∑iwi(f1[i]−f2[i]2)/(f1[i]+f2[i]) ,此时 f1 与 f2 为DeepFace人脸表示。其中运用于元素 (f1[i]−f2[i]2)/(f1[i]+f2[i]) 向量的权重参数根据使用线性支持向量机学习得到。
4.2 Siamese 网络
我们也在被称为Siamese网络的端对端矩阵学习方法中进行了测试:一旦进行了学习,一个人脸识别网络(除去最顶层)会被复制两次(一个输入图像使用一个网络)并且特征会被使用于直接预测两张输入图像是否属于同一个人。上述过程通过(a)特征之间采用绝对差异,(b)再将最高的全连接层映射到一个单独的逻辑单元(相同或不同)上来实现。因为该网络在两个复制品之间被分享,所以其与原先的网络有大概相同数量的参数,但仍需要两次计算。在人脸验证中为了避免过拟合线性,我们使训练只在最高两层进行。Siamese网络导出距离为: d(f1,f2)=∑iαi|f1[i]−f2[i]| ,此时 αi 为可训练的参数。Siamese网络中的参数被误差的标准交叉熵与反向传播方法所训练。
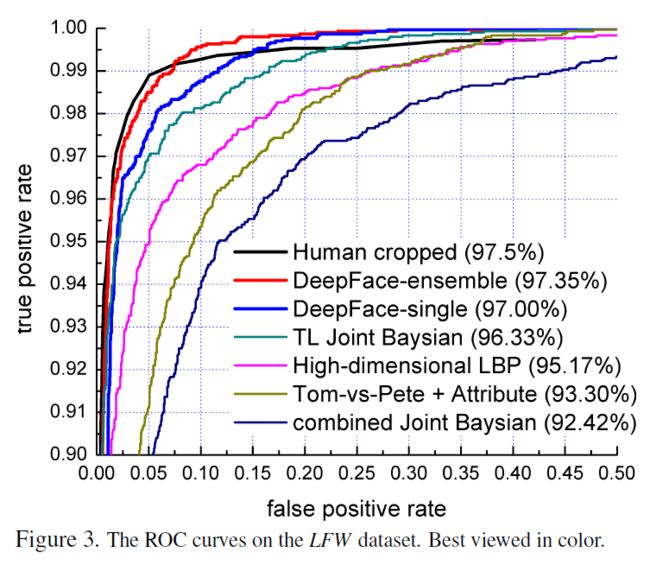
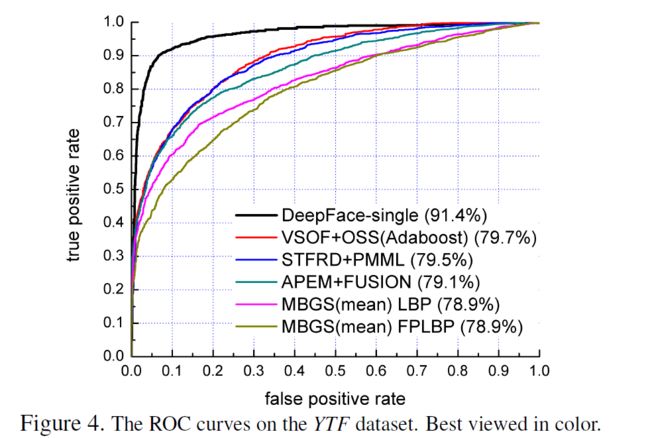
注:第五部分为实验结果分析,暂不翻译,感兴趣的朋友可以打开我所给的原文链接查看内容,部分结果贴图如下:
6. 总结
一个理想的人脸识别分类仅会准确识别到受人类匹配的面孔。底层人脸描述符将需要姿势,照明,表达,和图像质量的不变性。任何人在任何情况下应该可以将它在某种程度上进行细微调整后应用于各种各样的人群。此外,短描述符是优选的,并且如果可能的话,稀疏特征也是所希望得到的。当然,快速的计算时间也是一个问题。我们认为,这一从近期使用更多特征和更强大的度量学习技术的发展趋势中分离出来的工作已经解决了这一难题,大大减少了绝大多数这种性能差距。我们的工作表明,耦合基于3D模型的对准与大容量前馈模型可有效地从许多例子学会克服以前的方法的缺点和限制。呈现在面部识别显着改进的能力,证明了这种耦合的潜能将在其他视觉领域也会是显著的。