线段树详解
听完团队的一位大佬讲后颇有心得,写篇博客分享一下,希望能帮到大家。
首先要先知道线段树是什么?
线段树其实就是一颗树,与其他树不一样的是正常的树节点信息是一个,而线段树顾名思义是一段所以它每个节点有三个信息分别是左端点、右端点、线段的信息,这三样中只有信息是可以很多,左右端点是惟一的。这是大概理念,听不懂没关系,下面上个经典图就知道了。
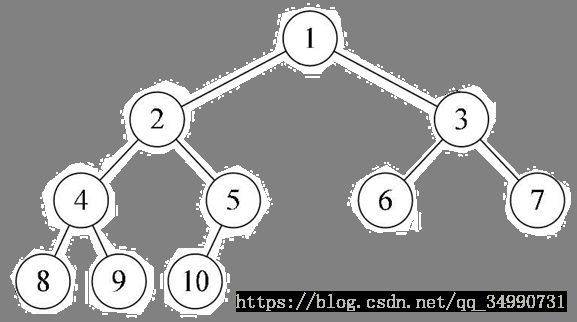
这是普通的树

这是线段树,而且是左闭右开区间,这里面还只有左右端点,区间信息还没有,不过已经很形象了。至于什么是左闭右开区间,就是[i,j)就这么写开是小括号,闭是中括号,意思就是从i到j这一区间包括i没有j(闭就是有包括,开是没包括,这些都是对于左右端点来说,中间的内容是都有的,不受这个影响,下面的模板代码都是左闭右开区间),与数学意义不同的是这些绝大部分都是整数。如果题目是左闭右闭的话要j++这样就是左闭右开了。
这个性质决定了线段树可以很好地解决区间修改查询问题。
意义讲完后现在讲一下怎么实现,线段树主要的是三个步骤,分别是建树、修改区间、访问区间值。
先讲建树,建树的方试有很多,链表、数组、堆、压缩堆(离散化)。其中各有千秋,比较推荐的是数组和压缩堆(离散化),原因是比较优点胜于缺点(个人认为),数组可以很好实现可空间有点浪费是O(4*n),而压缩堆(离散化)空间接近O(n)可实现比较麻烦,如果是初学者更推荐堆(实际上就是数组),如果是比赛的话堆还是优先考虑,如果计算后空间会炸的话再自己权衡。PS:一下模板代码是用堆的。
下面上代码:PS:模板代码是解区间和的,如果是其他题目只要稍微改一下就好了。
/**
使用堆结构存储若要访问儿子或父亲很方便
直接tree[p<<1] tree[p<<1|1] tree[p>>1]
*/
struct edge//我们用结构体实现线段树
{
long long l,r,tag,bj,sum;
}tree[400100];//记得开4倍!!!
这是定义树(用结构体加数组)
下面是建树的代码:
void build(long long x,long long l,long long r)//我们现在已经建树建到x点了,然后目前的区间是[l,r)
{
tree[x].l=l,tree[x].r=r,tree[x].tag=0,tree[x].bj=1,tree[x].sum=0;
if(r-l==1)//如果是叶节点
tree[x].sum=a[l];
else
{
long long mid=(l+r)>>1;//找到中间节点来划分左右儿子
build(x<<1,l,mid);
build((x<<1)|1,mid,r);
tree[x].sum=tree[x<<1].sum+tree[(x<<1)|1].sum;
}
return ;
}
建树搞定后下面讲区间修改
void change(long long x,long long l,long long r,long long k)//我们当前已经修改到了点x,然后目前区间是[l,r),修改的差值(即要加上多少)为k
{
if(l<=tree[x].l && r>=tree[x].r)//如果整个区间都是我们要修改的直接修改就好了
{
tree[x].sum+=k*(tree[x].r-tree[x].l);
tree[x].tag+=k;
}
else
{
long long mid=(tree[x].l+tree[x].r)>>1;
if(tree[x].tag!=0)//我们要下传懒标记
pass(x);
if(l<mid)
change(x<<1,l,min(mid,r),k);//这边我们取min(mid,r)的原因就是r有可能比mid小
if(mid<r)
change((x<<1)|1,max(mid,l),r,k);//同理
tree[x].sum=tree[x<<1].sum+tree[(x<<1)|1].sum;
}
return ;
}
这就用到了之前定义的一个标记tag,这是一个懒标记,如果不用的话修改时间将会是O(n*log n),竟然比暴力(O(n))时间还长,这显然不是我们要的,而这个懒标记可以强势地把时间复杂度降为O(log n),这个标记实际上就是把修改的值赋给它,当访问到这个节点是在及时修改并且下传至子节点,访问的方式有很多种,例如:修改、查询。是不是很奇妙。好好体会,一时没看懂没关系,多看几遍,动手写写,对于标记的用法在发一段代码帮助理解。PS:这段代码与线段树无关,只是体会一下这个懒标记。
void pass(long long x)
{
tree[x<<1].sum+=tree[x].tag*(tree[x<<1].r-tree[x<<1].l);//左区间修改一下
tree[x<<1].tag+=tree[x].tag;//左区间标记更新
tree[(x<<1)|1].sum+=tree[x].tag*(tree[(x<<1)|1].r-tree[(x<<1)|1].l);
tree[(x<<1)|1].tag+=tree[x].tag;
tree[x].tag=0;//清空本身标记
return ;
}
下面上查询的代码
long long ask(long long x,long long l,long long r)
{
if(l<=tree[x].l && r>=tree[x].r)//如果整个区间都是我们要查询的直接加就好了
return tree[x].sum;//回溯
else
{
long long mid=(tree[x].l+tree[x].r)>>1,ans=0;
if(tree[x].tag!=0)
pass(x);
if(l<mid)
ans+=ask(x<<1,l,min(mid,r));//一样
if(mid<r)
ans+=ask((x<<1)|1,max(mid,l),r);//The same
return ans;
}
}
以上就是线段树的实现代码。
给个经验,一般碰到线段树的题目,第一步确定线段树表示的区间的含义
,第二歩根据其含义确定线段树的定义形式,第三步根据问题确定线段树上要维护的信息, 确定信息是max型还是sigma型 ,第四步综合上述结果,写出维护的过程,第五步确定答案与维护信息之间的关系,写出查询的过程,这只是大佬讲的,我觉得挺好用的,如果你有你的解题过程最好,在此做个参考。
模板题
#include希望大家看完这篇博客可以对线段树有个理解。