Sudoku项目设计
Suduku项目设计
- 一.Github项目地址
- 二.开发时间预估
- 三.解题思路
- 项目要求
- 思考过程
- 生成终局
- 求解数独
- 四.设计实现过程
- 程序流程图
- 函数说明
- 函数流程图
- 五.单元测试
- 六.性能分析及改进
- 七.代码说明
- 生成终局关键代码
- 随机挖空生成数独题目代码
- 解数独关键代码
- 八.PSP表格
- 九.总结
- 附加题：SudokuGUI
- 功能介绍
- 具体设计
一.Github项目地址
https://github.com/BIT1120161750/Sudoku.
二.开发时间预估
| PSP2.1 | Personal Software Process Stages | 预估耗时（分钟） | 实际耗时（分钟） |
|---|---|---|---|
| Planning | 计划 | 10 | |
| · Estimate | · 估计这个任务需要多少时间 | 10 | |
| Development | 开发 | 1860 | |
| · Analysis | · 需求分析（包括学习新技术） | 120 | |
| · Design Spec | · 生成设计文档 | 60 | |
| · Design Review | · 设计复审（和同事审核设计文档） | 30 | |
| · Coding Standard | · 代码规范（为目前的开发制定合适的规范） | 30 | |
| · Design | · 具体设计 | 120 | |
| · Coding | · 具体编码 | 1200 | |
| · Code Review | · 代码复审 | 60 | |
| · Test | · 测试（自我测试，修改代码，提交修改） | 240 | |
| Reporting | 报告 | 270 | |
| · Test Report | · 测试报告 | 120 | |
| · Size Measurement | · 计算工作量 | 30 | |
| · Postmortem & Process Improvement Plan | · 事后总结，并提出过程改进计划 | 120 | |
| · | 合计 | 2140 |
三.解题思路
项目要求
本项目要求实现一个命令行程序，能够：
- 生成1~1e6个不重复的数独终局至文件。
- 读取文件内的数独问题，进行求解并将结果输出到文件。
思考过程
数独问题主要可以分为生成终局与求解数独两个部分。
生成终局
我在网上查阅了相关资料，了解到生成终局主要有暴力回溯法、矩阵转换法、行列交换法、随机化方法等。
以下给出一些生成终局的算法链接：
- 深度优先搜索和回溯法生成数独.
- 数独——高效生成算法
- 终盘生成之矩阵转换法
经过了解，回溯法生成终局最为简单，但是较为暴力。最终考虑采用利用全排列加行列变换生成终局。
首先需要生成一个种子盘。根据要求，左上角的第一个数字固定为（5+0）%9+1=6，求取第一行剩余8个数字的全排列，共8！=40320种，余下8行通过将第一行分别平移3、6、1、4、7、2、5、8格生成。这样我们就得到了种子盘。
根据已知规律，一个盘内{1，2，3}，{4，5，6}，{7，8，9}行/列组内任意互换，形成的仍然是一个符合要求的数独终局，由于左上角数字固定，第1行不参与交换，故每个种子盘可以生成2！* 3！* 3！= 72个不重复的终局。此时我们可以得到的终局个数为40320*72=2903040>1e6，已满足题目要求。
求解数独
求解数独最基本的思路为暴力搜索，除此外也有很多优秀的算法，例如回溯法，DLX等。以下给出一些求解数独的算法链接：
- Sudoku DLX 算法求解
- 数独求解算法
- Solving Every Sudoku Puzzle
一开始准备使用DLX算法，这是目前求解数独中较为高效的一种，但是因为对双向链表的操作不太熟悉，所以退而求其次选择了深搜+递归回溯法。
具体思路为顺序搜索整个盘面，找到未填入数字的空格，尝试填入一个数字，如果合法则进行下一步，直至填满整个棋盘。如果导致不合法，则回退到上一步。
约束条件：
- 81个格子中每个格子只能放一个数字
- 每一行的数字不能重复
- 每一列的数字不能重复
- 每一九宫内的数字不能重复
四.设计实现过程
程序流程图
Created with Raphaël 2.2.0 开始 输入指令 指令类型 求解数独 写入文件 结束 生成终局 yes no
函数说明
程序共分为5个模块
- main.cpp
本模块为主模块，是程序的对外接口，包含主函数main(),主要实现命令的输入及分析，对不符合要求的命令报错，实现终局的生成及求解数独。 - structure.cpp
本模块为结构定义模块，包含函数str_2_num()，用于将输入的指令转化为数字,函数print()，完成数独盘向文件的写入。主要实现输入输出功能。 - init.cpp
本模块为初始化模块，包含函数permutation(),init_origin()，用于全排列生成种子盘并进行初始化。 - generator.cpp
本模块为生成终局和生成题目模块，包含函数generate_sudoku(),基于种子盘通过交换行生成相应数量的终局并写入文件；函数generate_ques(),使用随机挖空生成数独题目并写入sudo.txt文件中。 - solver.cpp
本模块为解数独模块，包含函数slove_sudoku(),通过递归回溯求解数独。
函数流程图
Created with Raphaël 2.2.0 命令输入 Main() -c Generate_sudoku() Permutation() -s Solve_sudoku() Solution() Exit() yes no yes no
五.单元测试
单元测试的设计主要分两个方向，测试输入参数合法及不合法时程序的反应，测试生成的终局是否满足约束及题目所要求的格式。
共设计了12个单元测试。
代码覆盖率如下：
六.性能分析及改进
在本机生成1e6个终局的样本分析报告如下，共用时42s。
各函数占用资源情况如下
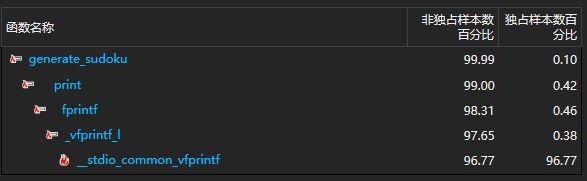
可以看到输出函数print（）占比较多，因为数独盘逐行写入文件较为费时，经过分析与测试，改为使用fputs()函数，将一个数独终局存入一个字符串，一次性写入文件。
此时在本机生成1e6个终局可以在5s内完成。
性能分析图如下：
可以看到此时输出函数puts()用时明显降低。
七.代码说明
生成终局关键代码
// 生成n个数独终局
// n:需求生成数独终局的数量
// 返回值：1:生成成功; -1:生成出错
int generate_sudoku(int n)
{
FILE *fp;
fp = fopen("sudoku.txt", "w");
int count = 0; // 计数，第一次不输出空行
BOARD board;
for (int i = 0; i < 40320; i++)
{
BOARD backup;
for (int k = 0; k < 9; k++)
{
backup.map[0][k] = origin[i][k];
backup.row[k] = 1022;
backup.col[k] = 1022;
backup.grid[k] = 1022;
}
for (int j = 1; j < 9; j++)
{
for (int k = 0; k < 9; k++)
backup.map[j][k] = backup.map[0][(k + shift[j]) % 9];
}
board = backup; // 初始构造
for (int j = 0; j < 6; j++)
{
for (int k = 0; k < 6; k++)
{
// 1~3行填充方案1
if (count < n)
{
fill(0, j, k, backup, board);
print(fp, board, count);
count++;
}
else if (count == n)
{
fclose(fp);
return 1; // 生成成功
}
else if (count >= n)
{
fclose(fp);
return -1; // 报错
}
// 1~3行填充方案2
if (count < n)
{
fill(1, j, k, backup, board);
print(fp, board, count);
count++;
}
else if (count == n)
{
fclose(fp);
return 1; // 生成成功
}
else if (count >= n)
{
fclose(fp);
return -1; // 报错
}
}
}
}
fclose(fp);
return -1; // 报错:输入n已经超过最大个数
}
上述代码基于第一行的全排列实现数独终局的生成。
随机挖空生成数独题目代码
void generate_ques(int n)
{
FILE *file1;
FILE *file2;
file1 = fopen("sudoku.txt", "r");
file2 = fopen("sudo.txt", "w");
int count = 0;
BOARD board;
int tmp;
while (~fscanf(file1, "%d", &tmp))
{
board.map[0][0] = tmp;
for (int j = 1; j < 9; j++)
{
fscanf(file1, "%d", &board.map[0][j]);
}
for (int i = 1; i < 9; i++)
{
for (int j = 0; j < 9; j++)
{
fscanf(file1, "%d", &board.map[i][j]);
}
}
int base[9] = { 0,6,12,54,60,66,108,114,120 };
int add[9] = { 0,2,4,18,20,22,36,38,40 };
for (int k = 0; k < 9; k++)//每个3*3随机掏空2个
{
int i, j, pos[2];
pos[0] = rand() % 9;
pos[1] = rand() % 9;
while (pos[0] == pos[1])//防止重复
pos[1] = rand() % 9;
for (int t = 0; t < 2; t++)
{
int dot;
dot = base[k] + add[pos[t]];
i = dot / 18;
j = dot % 18;
board.map[i][j] = 0;
}
}
//已经掏空了18个
int extra;
extra = 12 + rand() % 31;
while (extra--)
{
int k = rand() % 81;
int i = k / 9;
int j = k % 9;
j *= 2;
if (board.map[i][j] != 0)board.map[i][j] = 0;
else extra++;
}
//写入题库sudo.txt;
print(file2, board, count);
count++;
}
fclose(file1);
fclose(file2);
}
上述代码用于根据之前生成的sudoku.txt中存放的终局随机挖空生成数独题目，并写入sudo.txt文件中（整个棋盘挖空在30~60之间，每个小九宫格中挖空不少于两个）。
解数独关键代码
/// 读取题目并解出
void solve_sudoku(FILE *fp)
{
FILE *fp_w;
fp_w = fopen("sudoku.txt", "w");
int flag = 0;
BOARD board;
int tmp;
while (~fscanf(fp, "%d", &tmp)) {
board.map[0][0] = tmp;
for (int j = 1; j < 9; j++) {
fscanf(fp, "%d", &board.map[0][j]);
}
for (int i = 1; i < 9; i++) {
for (int j = 0; j < 9; j++) {
fscanf(fp, "%d", &board.map[i][j]);
}
}
solve_board(board);
BOARD backup = board;
solution(board, backup);
print(fp_w, board, flag);
flag = 1;
}
fclose(fp);
fclose(fp_w);
}
上述代码用于实现解数独。
八.PSP表格
| PSP2.1 | Personal Software Process Stages | 预估耗时（分钟） | 实际耗时（分钟） |
|---|---|---|---|
| Planning | 计划 | 10 | 15 |
| · Estimate | · 估计这个任务需要多少时间 | 10 | 15 |
| Development | 开发 | 1860 | 2240 |
| · Analysis | · 需求分析（包括学习新技术） | 120 | 210 |
| · Design Spec | · 生成设计文档 | 60 | 60 |
| · Design Review | · 设计复审（和同事审核设计文档） | 30 | 30 |
| · Coding Standard | · 代码规范（为目前的开发制定合适的规范） | 30 | 30 |
| · Design | · 具体设计 | 120 | 120 |
| · Coding | · 具体编码 | 1200 | 1450 |
| · Code Review | · 代码复审 | 60 | 40 |
| · Test | · 测试（自我测试，修改代码，提交修改） | 240 | 300 |
| Reporting | 报告 | 270 | 240 |
| · Test Report | · 测试报告 | 120 | 90 |
| · Size Measurement | · 计算工作量 | 30 | 30 |
| · Postmortem & Process Improvement Plan | · 事后总结，并提出过程改进计划 | 120 | 120 |
| · | 合计 | 2140 | 2490 |
九.总结
本次个人项目和我以前做过的项目有很大不同，coding过程不再是唯一的重点，还涉及到前期的计划、需求分析、设计文档，编码之后的复审、性能分析及改进、代码测试等，在这个项目中我第一次体验到了一个完整的软件项目开发所要经历的步骤。其间因为很多东西之前没有接触过，尤其是性能分析和软件测试，参考了很多资料进行学习后才能完成。通过这个过程，我对软件开发整体的认识变得更加全面，工程能力得到很大的提升。
另外本次项目需要用github进行代码管理，并用博客记录开发过程，之前并未有过将自己的程序或者项目上传的经历，就也没有体会到合理的代码管理以及适时的项目记录带来的好处。虽然配置vs和github的同步还有学习markdown语法都费了一些时间，但是感觉整个开发过程变得更加清晰有条理，思路也十分顺畅，在以后的项目开发过程中会继续对这两个工具加以利用。
总之，通过本次个人项目，我的工程能力、学习能力以及项目管理能力都得到了一定程度的提升，这也是我第一次从头到尾完整而独立地完成一个项目的开发，受益匪浅。
附加题：SudokuGUI
因还剩些许时间，故决定完成sudoku的游戏界面。首先要考虑的问题是采用何种工具进行图形界面开发。初步有三个想法：
- 利用C#编写Windows窗体应用程序，在小学期编写数据库实验的时候曾经使用过，有一定基础；
- 使用QT进行开发，相较winform而言更加专业，但是需要重头开始学习；
- 利用python的GUI库进行开发，语言较为简单，但是对相关的库不是特别熟悉。
出于对时间的考虑最后采用了第一种方案。
界面效果如下：
程序的题库来自通过sudoku.exe随机挖空生成的1000道题目（整个棋盘挖空在30~60之间，每个小九宫格中挖空不少于两个），存放在sudo.txt中
功能介绍
- Next按钮用随机生成一个数独题目，上图中浅粉色的textbox中即为生成的题目，不允许更改。
- 用户可以在9*9中空白格子里填写数字完成数独题目。
- Reset按钮用于清空玩家已填的数字，恢复初始题目。
- Submit按钮用于提交当前答案，若尚有格子未填，会给出“未完成”的提示；若填满但答案错误，会给出“回答错误的提示”；若答案正确，会给出“bingo~”的提示。
- Prompt按钮用于给出提示。
- Exit按钮用于退出游戏，当玩家点击时会弹出“确认退出？”的窗口，继续点击是，退出游戏，否则仍停留在游戏界面。
- 最右侧为计时器。当玩家点击Next按钮生成新题目时开始计时，点击Submit或Reset按钮时计时停止。
具体设计
Form左侧为81个Textbox控件，保存在一个ArrayList中。
中间位5个Button控件，分别实现对应的功能。
右侧为一个label控件，用于显示计时器。
核心代码实现如下：
- 生成题目：
private void Next_Click(object sender, EventArgs e)
{
StreamReader sr1 = new StreamReader(@"sudo.txt");
for(int k=0;k<10*flag;k++)
{
string lines = sr1.ReadLine();
}
for(int i=0;i<9;i++)
{
string line = sr1.ReadLine();
for(int j=0;j<9;j++)
{
TextBox tbx = tbxList[i * 9 + j] as TextBox;
if(line[2*j]=='0')
{
tbx.Text = "";
tbx.ReadOnly = false;
tbx.ForeColor = Color.Black;
tbx.BackColor = Color.Ivory;
}
else
{
tbx.Text = line[2 * j].ToString();
tbx.ReadOnly = true;
tbx.ForeColor = Color.Brown;
tbx.BackColor = Color.MistyRose;
}
}
}
flag++;
//手动设置Timer，开始执行
Mytimer.Start();
TimeCount = 0;
}
- 提交（判断是否完成盘面以及检查答案是否正确）
private void Submit_Click(object sender, EventArgs e)
{
//停止执行
Mytimer.Stop();
string[] submap;
submap = new string[10];
for(int i=0;i<9;i++)
{
submap[i] = "";
for(int j=0;j<9;j++)
{
TextBox tbx = tbxList[i * 9 + j] as TextBox;
if(tbx.Text=="")
{
MessageBox.Show("未完成", "提示");
return;
}
submap[i] += tbx.Text;
}
}
int[] row = { 0, 3, 6, 27, 30, 33, 54, 57, 60 };
int[] add = { 0, 1, 2, 9, 10, 11, 18, 19, 20 };
//检查答案是否正确
for (int i=0; i < 9;i++)
{
int[] count_r = new int[10];//一行中每个数字出现的次数
int[] count_c = new int[10];//一列中每个数字出现的个数
int[] count_g = new int[10];//一个小九宫格中每个数字出现的个数
//计数清零
for (int j=0;j<9;j++)
{
count_r[j] = 0;
count_c[j] = 0;
count_g[j] = 0;
}
//计数
for(int j=0;j<9;j++)
{
count_r[submap[i][j]-'0']++;
count_c[submap[j][i]-'0']++;
int pos = row[i] + add[j];
int m = pos / 9;
int n = pos % 9;
count_g[submap[m][n]-'0']++;
}
for(int j=1;j<9;j++)
{
if (count_r[j]==0 || count_r[j] > 1||count_c[j]==0||count_c[j]>1||count_g[j]==0||count_g[j]>1)
{
MessageBox.Show("回答错误！", "提示");
return;
}
}
}
MessageBox.Show("Bingo~", "通过提示");
}
- 清零
private void Reset_Click(object sender, EventArgs e)
{
for(int i=0;i<9;i++)
{
for(int j=0;j<9;j++)
{
TextBox tbx = tbxList[i * 9 + j] as TextBox;
if (tbx.ReadOnly==false)
tbx.Text = "";
}
}
//停止执行
Mytimer.Stop();