【机器学习（五）】从决策树到随机森林

目录

引言

Bagging

随机森林（RF）

随机森林的优点

随机森林的缺点

代码实现随机森林

---

上一篇：【机器学习（四）】决策树、ID3算法、C4.5算法、CART算法：原理，案例和代码

 

引言

上一文，笔者详细介绍了决策树（点此查看决策树：ID3、C4.5、CART），以及决策树在实际案例中的计算。本文将在决策树的基础上，详细介绍随机森林。因此，学习随机森林算法之前，需要学习决策树。

随机森林（Random Forest，RF），是最常用的集成学习方法之一，它的分类和回归性能是一些传统算法不能超越的。集成学习主要分为两种算法，分别是Bagging算法和Boosting算。

Bagging算法中，RF是其中一个典型的代表；Boosting算法中，adaboost算法是一个典型的代表。

Boosting算法通过级联多个弱分类器，调整分类效果差的若分类器的权重实现一个强分类器，对实例进行预测；Bagging则是通过组合多个弱分类器，通过多个弱分类器的投票或均值对实例进行预测。

Bagging

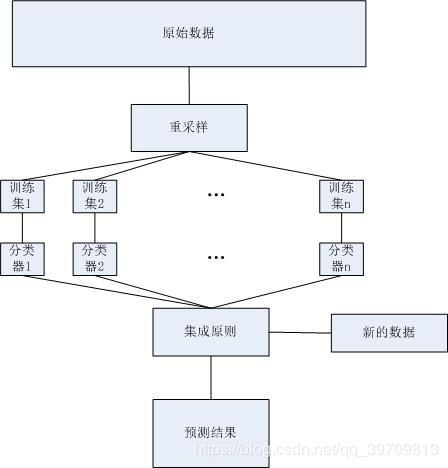
也成为自举汇聚法（bootstrap aggregating），如下图，指在原始的数据上，通过随机抽样的方式，选出K个新的数据作为弱分类器的训练数据，再组合多个弱分类器，构成一个强分类器。在做预测的时候，通过弱分类器投票或均值选择或计算结果。这种方法可以有效地降低过拟合的情况，增加模型的泛化能力。

自助法（bootstrap），即重采样。在原始的训练样本中有放回采集固定K个样本。采集后，这些样本将被放回原始数据中。结果就是：k个若分类器的训练样本，A个特征。这里k可能小于原始训练数据个数，A可能小于原始训练数据中的特征种类个数。

袋外数据（OOB），即没有被训练的数据。每次重采样后，原始的训练集中有部分数据没有被采样。这部分数据成为OOB（out of bag），这些没有参与训练的数据将会被用来测试模型的泛化能力。

RF输出，即随机森林最终的输出。随机森林可以用来解决回归问题或者分类问题。对于分类问题，RF最终的输出，是通过所有决策树的投票决定，票数最多的标签作为结果。对于回归问题，RF最终的输出，是通过对所有决策树求均值得到。

 

随机森林（RF）

随机森林是Bagging算法的一种。随机森林将原始的训练的数据，利用重采样的方式得到许许多多的子训练数据，每个子训练数据单独训练一个CART决策树（CART算法请点此查看：决策树：ID3、C4.5、CART）。如下图，可以看做一个森林，森林中有许多CART决策树，可每个决策树都是独立的，与其它树没有联合。

对于随机森林中的每个CART决策树，其特征个数是不确定的，依赖于采样的结果，一般情况下是特征总数的开方。

由于随机采样的作用，随机随机森林中的CART决策树往往不需要剪枝处理，也能够取得很好的抗过拟合；而决策树往往有着很好的训练精度，所以RF即有精度，又能防止过拟合。

 

随机森林的优点

RF不易过拟合，只要有足够多的决策树，RF模型就不会过拟合，增加了泛化能力。

随机森林中的决策树越多，模型预测的准确度就越高，同样预测的时间就越长（随着算法的改进，已经可以试下较短时的预测）

RF可以同时处理许多种不同属性的分类问题。

RF能够处理很高维度的数据，无论数据是连续还是离散，RF都能很好的适应，因此数据无需规范化处理。

RF的训练速度较快，相对来说，预测速度比训练速度慢。

RF中的每个决策树是独立存在的，因此可以采用并行运算的方法加快训练和预测。

RF实现简单，性能优越，在工业应用中使用较多。随机性的存在，使得RF模型具有一定的抗噪声能力

随机森林的缺点

RF内部的决策树很多的时候，模型规模就会很大，训练的时间和空间代价较大。

噪声比较多的样本里，RF容易陷入过拟合。因此训练数据至关重要。

 

代码实现随机森林

还是以决策树部分的案例为例子，使用机器学习库实现分类，代码如下：

from sklearn.ensemble import RandomForestClassifier
import numpy as np


def create_data():
    datasets = [[1, 0, 0, 1, 0],
                [1, 0, 0, 2, 0],
                [1, 1, 0, 2, 1],
                [1, 1, 1, 1, 1],
                [1, 0, 0, 1, 0],
                [2, 0, 0, 1, 0],
                [2, 0, 0, 0, 0],
                [2, 1, 1, 0, 1],
                [2, 0, 1, 3, 1],
                [2, 0, 1, 3, 1],
                [2, 0, 1, 3, 1],
                [2, 0, 1, 2, 1],
                [2, 1, 0, 2, 1],
                [2, 1, 0, 3, 1],
                [2, 0, 0, 1, 0],
                ]
    datasets = np.array(datasets)
    # 返回数据集和每个维度的名称
    return datasets[:, :4], datasets[:, -1]


train_x, train_y = create_data()
#  标准形式
# RandomForestClassifier(n_estimators=10, criterion='gini',
#                        max_depth=None, min_samples_split=2,
#                        min_samples_leaf=1, min_weight_fraction_leaf=0.0,
#                        max_features='auto', max_leaf_nodes=None,
#                        min_impurity_decrease=0.0, min_impurity_split=None,
#                        bootstrap=True, oob_score=False, n_jobs=1,
#                        random_state=None, verbose=0, warm_start=False,
#                        class_weight=None)
clf = RandomForestClassifier(n_estimators=10)
clf = clf.fit(train_x, train_y)
#  测试一个数据集
new = train_x[0, :]
print('new one:' + str(new))
print('预测结果为：', clf.predict(new.reshape(1, -1)))

随便找一个数据，得到的预测结果如下：

 

在此基础上，有一种改进的算法，称为极端随机森林。

实现代码如下：

from sklearn.ensemble import ExtraTreesClassifier
import numpy as np

def create_data():
    datasets = [[1, 0, 0, 1, 0],
                [1, 0, 0, 2, 0],
                [1, 1, 0, 2, 1],
                [1, 1, 1, 1, 1],
                [1, 0, 0, 1, 0],
                [2, 0, 0, 1, 0],
                [2, 0, 0, 0, 0],
                [2, 1, 1, 0, 1],
                [2, 0, 1, 3, 1],
                [2, 0, 1, 3, 1],
                [2, 0, 1, 3, 1],
                [2, 0, 1, 2, 1],
                [2, 1, 0, 2, 1],
                [2, 1, 0, 3, 1],
                [2, 0, 0, 1, 0],
                ]
    datasets = np.array(datasets)
    # 返回数据集和每个维度的名称
    return datasets[:, :4], datasets[:, -1]

train_x, train_y = create_data()
clf = ExtraTreesClassifier(n_estimators=10, max_depth=None,
                           min_samples_split=2, random_state=0)
clf = clf.fit(train_x, train_y)
#  测试一个数据集
new = train_x[3, :]
print('new one:' + str(new))
print('预测结果为：', clf.predict(new.reshape(1, -1)))

随便测试一组数据，结果如下：