Leetcode103 二叉树的锯齿形层次遍历 C++,Java,Python
Leetcode103 二叉树的锯齿形层次遍历
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/binary-tree-zigzag-level-order-traversal/
博主Github:https://github.com/GDUT-Rp/LeetCode
![]()
题目:
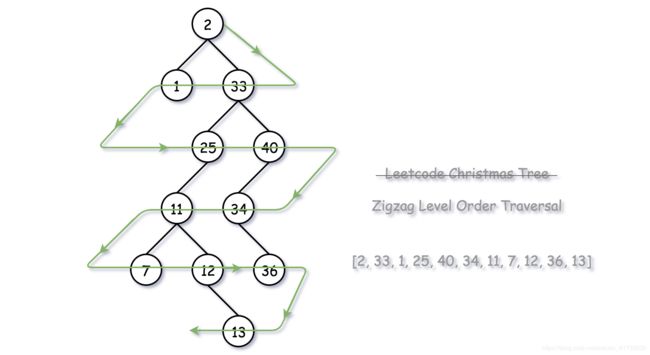
给定一个二叉树,返回其节点值的锯齿形层次遍历。(即先从左往右,再从右往左进行下一层遍历,以此类推,层与层之间交替进行)。
例如:
给定二叉树 [3,9,20,null,null,15,7],
3
/ \
9 20
/ \
15 7
返回锯齿形层次遍历如下:
[
[3],
[20,9],
[15,7]
]
解题思路:
方法一:BFS(广度优先遍历)
直观想法
最直观的方法是 BFS,逐层遍历树。
BFS 在每层的默认顺序是从左到右,因此需要调整 BFS 算法以生成锯齿序列。
最关键的是使用双端队列遍历,可以在队列的任一端插入元素。
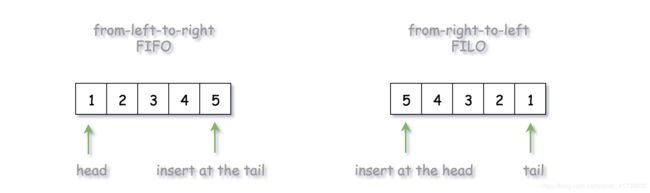
如果需要 FIFO (先进先出)的顺序,则将新元素添加到队列尾部,后插入的元素就可以排在后面。如果需要 FILO (先进后出)的顺序,则将新元素添加到队列首部,后插入的元素就可以排在前面。
算法
实现 BFS 的几种算法。
-
使用两层嵌套循环。外层循环迭代树的层级,内层循环迭代每层上的节点。
-
也可以使用一层循环实现 BFS。将要访问的节点添加到队列中,使用 分隔符(例如:空节点)把不同层的节点分隔开。分隔符表示一层结束和新一层开始。
这里采用第二种方法。在此算法的基础上,借助双端队列实现锯齿形顺序。在每一层,使用一个空的双端队列保存该层所有的节点。根据每一层的访问顺序,即从左到右或从右到左,决定从双端队列的哪一端插入节点。
- 实现从左到右的遍历顺序(FIFO)。将元素添加到队列尾部,保证后添加的节点后被访问。从上图中可以看出,输入序列
[1, 2, 3, 4, 5],按照 FIFO 顺序得到输出序列为[1, 2, 3, 4, 5]。 - 实现从右到左的遍历顺序(FILO)。将元素添加到队列头部,保证后添加的节点先被访问。输入序列
[1, 2, 3, 4, 5],按照 FILO 顺序得到输出序列为[5, 4, 3, 2, 1]。
C++
#include Java
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
public List<List<Integer>> zigzagLevelOrder(TreeNode root) {
if (root == null) {
return new ArrayList<List<Integer>>();
}
List<List<Integer>> results = new ArrayList<List<Integer>>();
// add the root element with a delimiter to kick off the BFS loop
LinkedList<TreeNode> node_queue = new LinkedList<TreeNode>();
node_queue.addLast(root);
node_queue.addLast(null);
LinkedList<Integer> level_list = new LinkedList<Integer>();
boolean is_order_left = true;
while (node_queue.size() > 0) {
TreeNode curr_node = node_queue.pollFirst();
if (curr_node != null) {
if (is_order_left)
level_list.addLast(curr_node.val);
else
level_list.addFirst(curr_node.val);
if (curr_node.left != null)
node_queue.addLast(curr_node.left);
if (curr_node.right != null)
node_queue.addLast(curr_node.right);
} else {
// we finish the scan of one level
results.add(level_list);
level_list = new LinkedList<Integer>();
// prepare for the next level
if (node_queue.size() > 0)
node_queue.addLast(null);
is_order_left = !is_order_left;
}
}
return results;
}
}
Python
# -*- coding: utf-8 -*-
# @File : LeetCode103.py
# @Author : Runpeng Zhang
# @Date : 2020/3/22
# @Desc : 二叉树的锯齿形层次遍历
from collections import deque
# Definition for a binary tree node.
class TreeNode:
def __init__(self, x):
self.val = x
self.left = None
self.right = None
class Solution:
def zigzagLevelOrder(self, root: TreeNode):
"""
:type root: TreeNode
:rtype: List[List[int]]
"""
ret = []
level_list = deque()
if root is None:
return []
# start with the level 0 with a delimiter
node_queue = deque([root, None])
is_order_left = True
while len(node_queue) > 0:
curr_node = node_queue.popleft()
if curr_node:
if is_order_left:
level_list.append(curr_node.val)
else:
level_list.appendleft(curr_node.val)
if curr_node.left:
node_queue.append(curr_node.left)
if curr_node.right:
node_queue.append(curr_node.right)
else:
# we finish one level
ret.append(list(level_list))
# add a delimiter to mark the level
if len(node_queue) > 0:
node_queue.append(None)
# prepare for the next level
level_list = deque()
is_order_left = not is_order_left
return ret
复杂度分析
时间复杂度: O ( N ) \mathcal{O}(N) O(N),其中 N 是树的结点数,因为每个结点都访问一次。
空间复杂度: O ( N ) \mathcal{O}(N) O(N),其中 N 是树中节点的数量。
除了输出数组,主要的内存开销是双端队列。
任何时刻,双端队列中最多只存储两层节点。因此双端队列的大小不超过 2 ⋅ L 2 \cdot L 2⋅L,其中 LL 是一层的最大节点数。包含最多节点的层可能是完全二叉树的叶节点层,大约有 L = N 2 L = 2 N L = \frac{N}{2}L= 2N L=2NL=2N个节点。因此最坏情况下,空间复杂度为 2 ⋅ N 2 = N 2 \cdot \frac{N}{2} =N 2⋅2N=N。
方法二:DFS (深度优先遍历)
直观想法
也可以使用 DFS 实现 BFS 的遍历顺序。
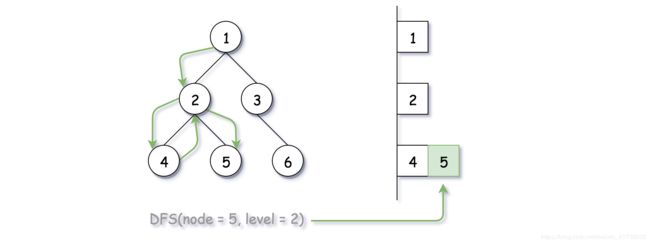
在 DFS 遍历期间,将结果保存在按层数索引的全局数组中。即元素
array[level]存储同一层的所有节点。然后在 DFS 的每一步更新全局数组。
与改进的 BFS 算法类似,使用双端队列保存同一层的所有节点,并交替插入方向(从首部插入或从尾部插入)得到需要的输出顺序。
算法
使用递归实现 DFS 算法。定义一个递归方法 DFS(node, level),方法参数为当前节点 node 和指定层数 level。该方法共执行三个步骤:
-
如果是第一次访问该层的节点,即该层的双端队列不存在。那么创建一个双端队列,并添加该节点到队列中。
-
如果当前层的双端队列已存在,根据顺序,将当前节点插入队列头部或尾部。
-
最后,为每个节点调用该递归方法。
C++
#include Java
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
protected void DFS(TreeNode node, int level, List<List<Integer>> results) {
if (level >= results.size()) {
LinkedList<Integer> newLevel = new LinkedList<Integer>();
newLevel.add(node.val);
results.add(newLevel);
} else {
if (level % 2 == 0)
results.get(level).add(node.val);
else
results.get(level).add(0, node.val);
}
if (node.left != null) DFS(node.left, level + 1, results);
if (node.right != null) DFS(node.right, level + 1, results);
}
public List<List<Integer>> zigzagLevelOrder(TreeNode root) {
if (root == null) {
return new ArrayList<List<Integer>>();
}
List<List<Integer>> results = new ArrayList<List<Integer>>();
DFS(root, 0, results);
return results;
}
}
Python
# -*- coding: utf-8 -*-
# @File : LeetCode103.py
# @Author : Runpeng Zhang
# @Date : 2020/3/22
# @Desc : 二叉树的锯齿形层次遍历
from collections import deque
# Definition for a binary tree node.
class TreeNode:
def __init__(self, x):
self.val = x
self.left = None
self.right = None
class Solution:
def zigzagLevelOrder(self, root: TreeNode):
"""
:type root: TreeNode
:rtype: List[List[int]]
"""
if root is None:
return []
results = []
def dfs(node, level):
if level >= len(results):
results.append(deque([node.val]))
else:
if level % 2 == 0:
results[level].append(node.val)
else:
results[level].appendleft(node.val)
for next_node in [node.left, node.right]:
if next_node is not None:
dfs(next_node, level + 1)
# normal level order traversal with DFS
dfs(root, 0)
for i, enum in enumerate(results):
results[i] = list(results[i])
return results
算法复杂度:
时间复杂度:访问每个节点恰好一次,时间复杂度为 O ( N ) O(N) O(N) ,其中 N N N 是节点的个数,也就是树的大小。
空间复杂度:取决于树的结构,最坏情况存储整棵树,因此空间复杂度是 O ( N ) O(N) O(N)。