数据结构与算法(Python)——常见数据结构Part4(二叉树)
写在前面
在上一节part3我们熟悉队列结构,本节将熟悉应用广泛的树结构。我们的目的是快速了解他们,对于它们涉及到的复杂的数据结构和算法,在这里并不全部展开,留在后期详述。
1. 树
1.1 树的直观感受
树是一个广泛应用的数据结构,即使未开始学习这个数据结构,我们在生活或者计算机中已经和它打交道好久了。首先让我们看几个树形的应用例子(图片来自What is the real life application of tree data structures?):
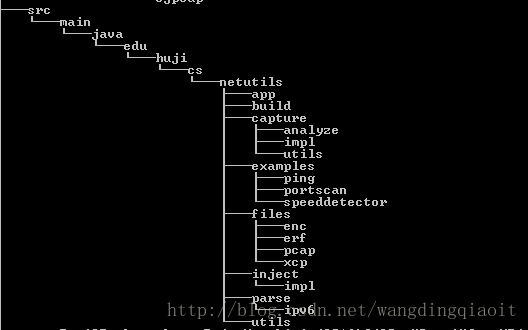
这里显示的是Windows系统下文件夹的目录结构,从src目录开始,整个目录结构构成一棵树(使用Windows命令tree可以查看文件目录结构)。
上图展现的是Linux文件系统构成的一棵树。
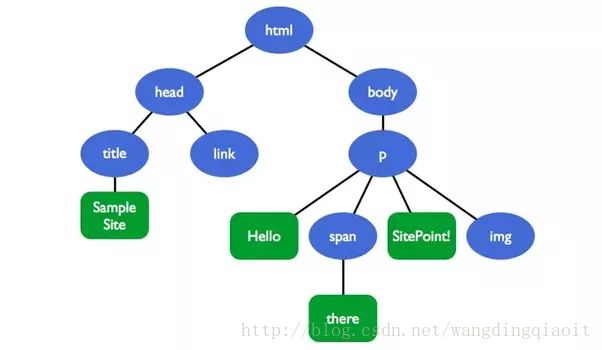
上图图展现的是HTML文档树,文档结点html及其下的其他结点构成了一棵树结构。
上图展示的是井字棋游戏中,人机对战时,机器从当前棋局状态推算出的下一状态构成的树形结构。
例子还有更多,通过上面的例子,我们已经对树形结构有了一个直观感受。下面我们看下计算中如何定义这个数据结构。
1.2 树的定义
在数据结构中,树被定义为这样一种结构:
- 在树中有一个特殊的结点,称作根结点(Root Node),他没有父结点或者称为前驱结点(predecessor)。
- 在树中出了根以外,每个结点都有一个父结点。
- 树中所有结点有0个后者多个后继结点(successors)。
需要注意的是树与之前学习的数组、链表、栈以及队列不同,它不是一种线性结构,而是一种层次结构(hierarchical structure )。
数据结构中的树,抽象表示为(图片来自DATA STRUCTURES-TREE):
1.3 树相关的术语
了解树相关的术语对于后续学习很有必要,涉及到的术语包括下列内容(术语部分图片均来自DATA STRUCTURES-TREE)。
1) 根结点(Root)、孩子结点(Child)、父结点(Parent)

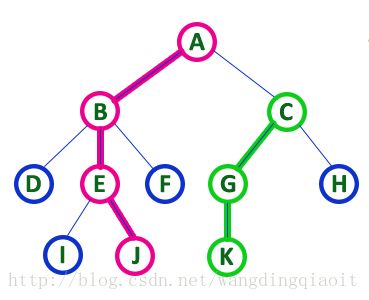
在上面的图中A结点称之为树的根结点,它是树形开始的起点;在树中一个结点的后继称之为这个结点的孩子结点,同时这个结点本身称之为它的孩子结点的父结点,例如图中根结点A有两个孩子结点B和C,B和C有一个共同的父结点A。结点K的父结点是G,同时G的父结点是C,可以看出这种层次关系。
2) 兄弟结点(Siblings)

同一个父结点的孩子结点之间的关系称之为兄弟结点,例如杀那个图中D、E、F结点称之为兄弟结点,它们共同的父结点为B;G和H结点也称之为兄弟结点,它们共同的父结点为C。
3) 叶子结点(Leaf node)、 内部和外部结点(Internal and external Nodes)
至少有一个孩子结点的结点称之为内部结点(Internal nodes),一个孩子结点都没有的结点称之为孩子结点(Leaf node),也称之为外部结点(External node)或者终端结点(Terminal Node)。
上面的图中亮色显式的都是内部结点,暗色显式的都是叶子结点。
4) 边(Edge)
边是连接两个结点的这条链接,如下图所示:
5) 入度(In Degree)和出度(Out Degree)
树中指向一个结点的边的数目称之为结点的入度,从一个结点指出的边的数目称之为结点的出度。根结点的入度总是为0,叶子结点的出度总是为0。
图中A结点的入度为0,出度为2;B结点的入度为1,出度为3;F结点的入度为1,出度为0。
注意,很多教材或者网站,在使用这个概念时并没有区分入度和出度,将出度,也就是结点拥有的子树数量称之为结点的度。
6) 层次(Level)
在树中根结点作为开始层,一般记为0,根结点的孩子结点记为层次1,依次类推,下一层记为2,…。注意某些情形下,根结点层次也可能记为从1开始。
7) 高度(Height)
结点的高度定义为从叶子结点到这个结点的最长路径中边的数量。叶子结点的高度记为0。树的高度定义为根结点的高度。
8) 深度(Depth)
树中从根结点到指定结点的路径上边的数量称为这个指定结点的深度。根结点的深度定义为0。一棵树的深度定义为从根结点到叶子结点的所有深度中的最大值。

9) 路径(Path)
树中从一个结点到另一个结点的所有边和结点称之为路径,路径的长度为其中结点的数量。
例如上图中,结点A和J之间路径为: A-B-E-J,长度为4。
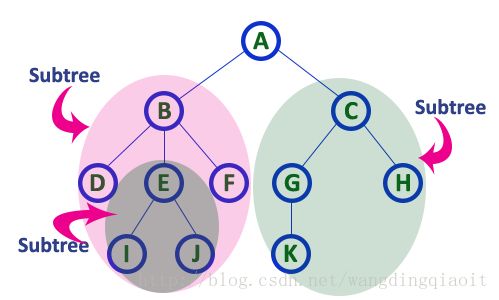
10) 子树(Subtree)
在树中,当前结点的孩子结点及孩子结点的后继构成的树,称之为当前结点的子树。这个概念是递归的。
上面的图中结点A有两个子树,结点B有3个子树。
1.4 树的种类
树是数据结构学科中广泛应用,有着多个变种的重要数据结构。其中既有简单的二叉树结构,也包括AVL(一种自平衡的二叉搜索树)、RBT(红黑树)、BTree(一种允许有多个孩子结点的二叉搜索树)等复杂的数据结构,完整的列表可以查看wiki-tree。
在常见数据结构部分,本节我们重点熟悉二叉树(binary trees)、二叉搜索树( binary search trees )、堆(Heap)三种类型的树,对于其他更为复杂的数据结构,我们将留在高级数据结构部分学习。
2. 二叉树
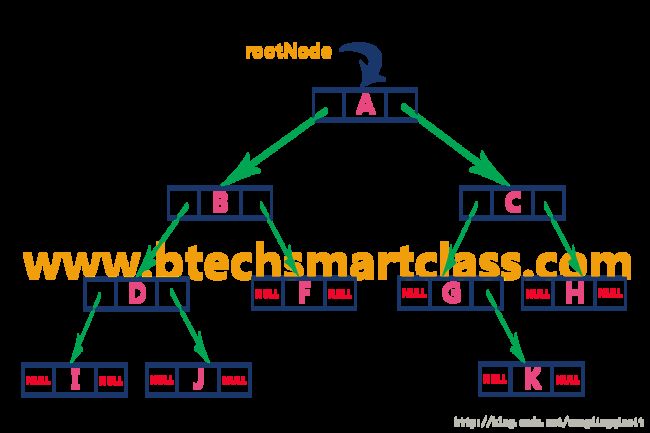
二叉树是每个结点最多有两个孩子的树,是一种常见的树形。例如下图所示为一个二叉树:
2.1 二叉树的性质
了解二叉树的性质,对于分析二叉树形态、算法复杂度很有帮助,下面简述几个重要性质,参考自二叉树性质。
1) 性质1 二叉树第i层上的结点数目最多为 2i−1(i≥1) 2 i − 1 ( i ≥ 1 )
第一层为根结点,i=1,此时满足上述公式;可以通过归纳法证明上述公式,证明留给读者自行证明。
2) 性质2 深度为k的二叉树至多有 2k−1(k≥1) 2 k − 1 ( k ≥ 1 ) 个结点
由性质1, 求和可得: 20+21+…+2k−1=2k−1 2 0 + 2 1 + … + 2 k − 1 = 2 k − 1
3) 性质3 在任意-棵二叉树中,若终端结点的个数为 n0 n 0 ,度为2的结点数为 n2 n 2 ,则 no=n2+1 n o = n 2 + 1 。
记树中结点总数为n,则有:
n=n0+n1+n2(1) (1) n = n 0 + n 1 + n 2
另一方面,除了根结点外,每个结点都是有父结点的, n0 n 0 不产生子结点, n1 n 1 结点产生一个子结点, n2 n 2 产生两个孩子结点,则有:
n−1=n1+2n2(2) (2) n − 1 = n 1 + 2 n 2
由式(1)和式(2)得出: no=n2+1 n o = n 2 + 1
二叉树中,如果一棵深度为 k k 且有 2k−1 2 k − 1 个结点的二叉树则称之为满二叉树(Full Binary Tree),满二叉树有两个特点:
(1) 每一层上的结点数都达到最大值。即对给定的高度,它是具有最多结点数的二叉树。
(2) 满二叉树中不存在度数为1的结点,每个分支结点均有两棵高度相同的子树,且树叶都在最下一层上。
对满二叉树的结点从上到下,从左到右编号为 1..n 1.. n ,可以引出完全二叉树的概念。如果一个深度为 k k ,有 n n 个结点的二叉树,当且仅当其每个结点都与深度为k的满二叉树中编号为1到n的结点一一对应时,称之为完全二叉树(Complete Binary Tree)。完全二叉树的特点:
(1) 叶子结点只可能出现在层次最大的两层
(2) 对于任一结点,若其右分支下子孙的最大层次为 l l ,则其左分支下子孙的最大层次为 l l 或者 l+1 l + 1 。
(3) 满二叉树是完全二叉树,完全二叉树不一定是满二叉树。
(4) 在满二叉树的最下一层上,从最右边开始连续删去若干结点后得到的二叉树仍然是一棵完全二叉树。
(5) 在完全二叉树中,若某个结点没有左孩子,则它一定没有右孩子,即该结点必是叶结点。
4) 性质4:具有n个结点的完全二叉树的深度为 floor(logn)+1 f l o o r ( l o g n ) + 1 .
证明: 设所求深度为 k k ,深度为 k k 的完全二叉树则 k−1 k − 1 层以前构成一棵满二叉树,节点个数为 2k−1−1 2 k − 1 − 1 ,而在第k层上还有若干节点,则有:
n>2k−1−1(a) (a) n > 2 k − 1 − 1
另一方面根据性质2,节点数目n满足:
n≤2k−1(b) (b) n ≤ 2 k − 1
根据上面两个式子,得出:
2k−1−1<n≤2k−1(c) (c) 2 k − 1 − 1 < n ≤ 2 k − 1
则有:
2k−1≤n<2k(d) (d) 2 k − 1 ≤ n < 2 k
上式两边同时取对数,则有:
k−1≤logn<k(e) (e) k − 1 ≤ l o g n < k
因为k-1和k是两个相邻整数,则有: k=floor(logn)+1. k = f l o o r ( l o g n ) + 1.
2.2 二叉树的实现
二叉树的存储可以由一维数组表示,例如上图中的二叉树用线性数组表示为:
这种方式的优点是访问结点时,可以通过序号索引,一个结点的孩子结点,可以通过计算索引得到,但缺点也很明显,结点为空时仍然占用了空间,另一种方式是采用链式存储,每个结点的结构如下图所示:
通过保存左孩子和右孩子的地址,构成了一个复杂的指针链,这样仅在需要的时候分配空间,但是访问元素则变得麻烦了。链式存储时二叉树结构如下图所示:
我们定义二叉树的结点如下:
class TreeNode(object):
"""
二叉树结点
"""
def __init__(self, data, left=None, right=None):
self.data = data
self.left, self.right = left, right
def __str__(self):
return str(self.data)
def __repr__(self):
return self.__str__()定义二叉树如下:
class BinaryTree(object):
"""
二叉树
"""
def __init__(self):
self.root = None定义一个从完全二叉树数组构造二叉树的初始化方法:
def __init__(self, data_array):
if type(data_array) is not list:
raise ValueError("init with complete tree data array only.")
if not data_array:
self.root = None
return
tree_nodes = [(x and TreeNode(x)) or None for x in data_array]
self.root = tree_nodes[0]
for i in range(0, len(data_array)-2 / 2 + 1):
if not tree_nodes[i]:
continue
if 2*i + 1 < len(tree_nodes):
tree_nodes[i].left = tree_nodes[2*i + 1]
if 2*i + 2 < len(tree_nodes):
tree_nodes[i].right = tree_nodes[2*i + 2]例如上面的二叉树,我们可以通过数组构造:
if __name__ == "__main__":
data_val_list = ['A', 'B', 'C', 'D', 'F', 'G', 'H', 'I', 'J', None, None, None, 'K', None, None]
binary_tree = BinaryTree(data_val_list)2.3 二叉树的遍历
遍历一棵二叉树时,可以从上到下,从左到右的遍历,这种方式称之为广度优先遍历(Breadth First Traverse); 另外我们还可以采用深度优先的遍历,深度优先遍历时尽可能多的遍历一个结点和它的子结点,这个结点完了之后再遍历其他结点。在深度优先遍历过程中有三个子任务即:
- V 访问根结点
- L 遍历左子树
- R 遍历右子树
上面3个顺序的排列一共有6种,限定遍历左子树优先右子树,则一共有三种遍历方式:
VLR 先序遍历(Pre - Order Traversal ( root - leftChild - rightChild ))
LVR 中序遍历(In - Order Traversal ( leftChild - root - rightChild ))
LRV 后序遍历(Post - Order Traversal ( leftChild - rightChild - root ))
广度优先遍历可以借助前面学习的队列结构实现:
def breadth_first_traverse(self, traverse_func, func_param=None):
"""
广度优先遍历 使用队列辅助实现
:param traverse_func: 遍历函数
:param func_param: 遍历函数的参数
:return: None
"""
if not self.root:
return
queue = [self.root]
while queue:
front_node = queue.pop(0)
traverse_func(front_node, func_param)
if front_node.left:
queue.append(front_node.left)
if front_node.right:
queue.append(front_node.right)对于上图中广度优先遍历输出结果为:
BinaryTree BreadthFirst [A,B,C,D,F,G,H,I,J,K]对于深度优先的遍历,可以使用递归实现,也可以借助栈来进行迭代实现。这里我们仅说明下中序遍历的递归和迭代实现,其余的遍历可以自行实现,或者参考源代码。
中序遍历的递归实现:
def in_order_traverse_by_recursion(self, traverse_func, func_param=None):
"""
中序遍历 leftChild - root - rightChild
:param traverse_func: 遍历函数
:param func_param: 遍历函数的参数
:return: None
"""
BinaryTree.__in__order_traverse(self.root, traverse_func, func_param)
@staticmethod
def __in__order_traverse(node, traverse_func, func_param):
if not node:
return
if node.left:
BinaryTree.__in__order_traverse(node.left, traverse_func, func_param)
traverse_func(node, func_param)
if node.right:
BinaryTree.__in__order_traverse(node.right, traverse_func, func_param)通过分析遍历过程,我们可以看出中序遍历的过程为: 1)从根结点开始,寻找当前结点的左孩子,直到找不到左孩子,2) 访问最后这个找不到左孩子的结点,然后往父结点退一步,访问父结点,然后对父结点的右孩子重复步骤1。这一过程中,总是先访问最左孩子,然后回退访问父结点,这个特性,很符合之前讲述的栈的记忆特性,因此可以借助栈来实现。
中序遍历借助栈的迭代实现:
def in_order_traverse_by_stack(self, traverse_func, func_param=None):
"""
中序遍历非递归实现 使用栈辅助实现
算法思想:
1) 将根结点设为当前待“归左”的结点
2) 对待归左结点持续将左孩子结点入栈,直至左孩子为空,转步骤3
3) 持续出栈,访问栈顶元素,直至当栈顶元素有右孩子时,
将右孩子设为待“归左”结点,转步骤2;出栈过程中栈为空,则结束
:param traverse_func: 遍历函数
:param func_param: 遍历函数的参数
:return: None
"""
if not self.root:
return
stack = []
node = self.root
while node:
while node:
stack.append(node)
node = node.left
next_process_node = None
while stack and not next_process_node:
node = stack.pop(-1)
traverse_func(node, func_param)
next_process_node = node.right
node = next_process_node对于先序和后序,也有类似实现,此处不再展开。使用栈的迭代版本实现时要求对树的遍历特性有较深的认识,通过栈来维持树遍历时访问各个结点的先后顺序达到递归遍历的效果。
除了递归和借助栈实现遍历外,还可以采用一种特殊的方法:在遍历过程中修改树的结构,使得结点没有左孩子,然后又恢复树结构的方法,这个算法由Joseph M.Morris开发。算法描述为:
def in_order_traverse_by_morris(self, traverse_func, func_param=None):
"""
Joseph M. Morris 中序遍历算法
不使用递归和栈实现的遍历算法
在遍历过程中修改和恢复树结构的方法
算法思想:
1) 如果树为空则返回,否则current = root,current表示当前结点
2) 对于每个current
如果current左孩子为空,则访问current,并将其右孩子赋给current
否则:
迭代取current的左孩子的最右边孩子tmp
如果tmp是current的临时父节点,则访问current并解除临时父子关系,
并将current右孩子赋给current
否则将tmp置为current的临时父节点,并将current的左孩子赋给current
3) 持续2过程直到current为空
:param traverse_func: 遍历函数
:param func_param: 遍历函数参数
:return: None
"""
cur_node = self.root
while cur_node:
if not cur_node.left:
traverse_func(cur_node, func_param)
cur_node = cur_node.right
else:
tmp = cur_node.left
while tmp.right and tmp.right != cur_node:
tmp = tmp.right
if not tmp.right:
tmp.right = cur_node
cur_node = cur_node.left
else:
traverse_func(cur_node, func_param)
tmp.right = None
cur_node = cur_node.right算法遍历的过程,可以参考下面的例子(来自《Data Structures and Algorithms in C++》 Adam Drozdek [Fourth Edition]):
上述中序遍历,也可以自行实现并在LeetCode在线OJ练习。
用4种方式遍历上面的二叉树,我们得到访问输出:
BinaryTree PreOrder [A,B,D,I,J,F,C,G,K,H]
BinaryTree InOrder [I,D,J,B,F,A,G,K,C,H]
BinaryTree PostOrder [I,J,D,F,B,K,G,H,C,A]
BinaryTree BreadthFirst [A,B,C,D,F,G,H,I,J,K]2.4 二叉树的可视化
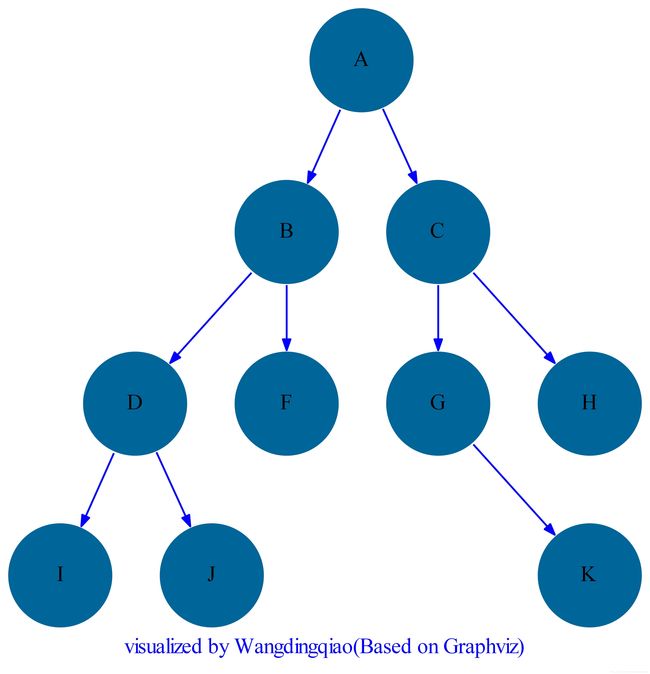
可视化二叉树能够帮助我们快速观察树形,对比数据。可视化可以借助Graphviz程序实现,Python第三方库Graphviz在系统安装了Graphviz程序时,结合自己编码也可以可视化一棵树。上面的可视化程序,可以在我的github下载。
2.5 二叉树与逆波兰式
我们通常见到的表达式,例如: a+b∗(c−d)−e/f a + b ∗ ( c − d ) − e / f 这种书写习惯符合我们阅读习惯,但因为要处理括号以及计算优先级和运算符的结合性等问题而难以解析和计算,因而产生了波兰表达式(Polish notation)和逆波兰表达式(reverse Polish notation (RPN))。
波兰表达式的特点是运算符在两个操作数的前面,而逆波兰式中运算符总是在两个操作数的后面,例如 (5−6)×7 ( 5 − 6 ) × 7 表达式的波兰表达式为:x-567,逆波兰式为:56-7*。波兰表达式的优势是计算时不需要括号,因而成为计算表达式的一种简便方法。
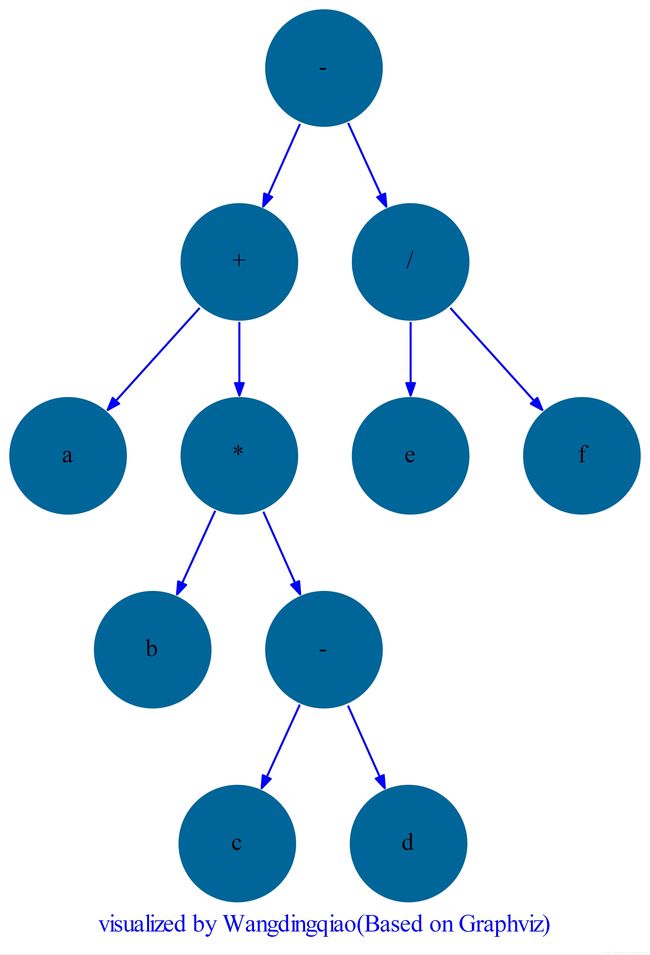
下面我们看一下表达式 a+b∗(c−d)−e/f a + b ∗ ( c − d ) − e / f 表示为一棵二叉树后效果:
先序、中序、后序遍历这棵二叉树,得到三个序列分别是:
BinaryTree PreOrder [-,+,a,*,b,-,c,d,/,e,f] # 前缀表示 即波兰式
BinaryTree InOrder [a,+,b,*,c,-,d,-,e,/,f] # 中缀表示
BinaryTree PostOrder [a,b,c,d,-,*,+,e,f,/,-] # 后缀表示 即逆波兰式从逆波兰式构建一棵二叉树的算法,简要描述为:
1)初始化一个栈
2)逐个读取逆波兰式字符串中字符,当前字符为操作数或者变量时,则新建一个结点入栈;当前字符为运算符,则新建一个结点,同时出栈两个元素作为这个新建结点的左右孩子,最后将这个新建结点入栈。
通常计算一个表达式,可以分为两个步骤:首先将表达式转换为逆波兰式,然后计算逆波兰式,从而求出整个表达式的值。这个计算过程中需要处理运算符的结合性,优先级,感兴趣地可以提前参考shunting-yard algorithm算法,在算法部分我们也将会学习这个算法,求解任意表达式的值。
关于二叉树还包括线索二叉树,这个应用的时候可以再回过头来学习,另外应用上还包括哈夫曼编码,回溯法等问题,我们也留在算法阶段学习。
本节先学习到这里,下节继续未完成的树主题。