期权Greeks(Delta、Gamma、Vega、Theta) 介绍与Python实现
期权希腊字母度量了不同因素的变化对期权价格的影响。现将主要希腊字母的含义、计算与实现方法以及一些业内常用处理方式总结如下。
文章目录
- 1. Delta
- 定义与计算
- 意义与用法
- 2. Gamma
- 定义与计算
- 意义与用法
- 3. Vega
- 定义与计算
- 意义与用法
- 4. Theta
- 定义与计算
- 意义与用法
- 5. Python实现
- 参考
1. Delta
定义与计算
Delta衡量期权理论价值相对于标的资产价格的变化率, Δ = ∂ V ∂ S \Delta =\frac{\partial V}{\partial S} Δ=∂S∂V。
基于BS Model,欧式期权,无分红下Delta的计算公式为:
| Call | Put |
|---|---|
| Δ = Φ ( d 1 ) \Delta =\Phi (d_{1}) Δ=Φ(d1) | Δ = − Φ ( − d 1 ) \Delta =-\Phi (-d_{1}) Δ=−Φ(−d1) |
其中,
- d 1 = l n ( S / K ) + ( r + σ 2 / 2 ) τ σ τ d_{1} = \frac{ln(S/K) + (r + {\sigma ^{2}}/2)\tau }{ \sigma\sqrt{\tau } } d1=στln(S/K)+(r+σ2/2)τ;
- Φ \Phi Φ是标准正态分布的累积分布函数, Φ ( x ) = 1 2 π ∫ − ∞ x e − y 2 2 d y \Phi (x) = \frac{1}{\sqrt{2 \pi}}\int_{-\infty}^{x }e^{-\frac{y^{2}}{2}}dy Φ(x)=2π1∫−∞xe−2y2dy;
- S S S为标的资产价格;
- K K K为行权价;
- r r r为无风险利率,实际常用一年期国债利率来表示;
- τ = T − t \tau=T-t τ=T−t,表示距离到期日的时间。实际常将单位转化为年,例如,距离到期日还有25天,则 τ = 25 / 365 = 0.068 \tau=25/365=0.068 τ=25/365=0.068;
- σ \sigma σ为标的资产的历史波动率。例如,计算50ETF期权的Greeks时, s i g m a sigma sigma常用过去60天50ETF对数收益率的标准差,再将其年化后来表示。
意义与用法
认购期权的Delta值介于0到1之间,认沽期权的值介于-1到0之间。越实值的期权,Delta的绝对值越接近于1,越虚值的期权,Delta的绝对值越趋近于0,平值期权的Delta的绝对值为0.5。基于这一特性,也常把Delta看作期权到期时实值的概率。
Delta具有可加性,可以被用来衡量头寸风险。例如,买入delta为0.5的A期权2张和delta为-0.4的B期权1张,那么总体持仓的风险状况可以表示为: 0.5 ∗ 2 − 0.4 = 0.6 0.5*2-0.4=0.6 0.5∗2−0.4=0.6,这是一个多头头寸。
对于交易者来说,Delta也常代表着Delta中性策略的对冲比率,只要使头寸的整体Delta值保持为0,那么就建立了一个中性的套保策略。例如,1份ETF期权多头需要用Delta份ETF空头来对冲。
最后,可以用Delta来计算杠杆。我们知道期权具有一定的杠杆性,比如ETF上涨1%,期权上涨10%,那么期权的杠杆就是10倍。通过Delta,我们可以计算期权的杠杆倍数。假设目前50ETF的价格是3.000元,有一份期权现在的价格是0.100元,Delta为0.33。如果ETF上涨1%,也就是0.03元,期权价格就会上涨0.03*Delta,等于0.01元。从涨幅来看,期权合约上涨了10%。因此,期权合约的杠杆大概是10倍。
2. Gamma
定义与计算
Gamma衡量期权Delta相对于标的资产价格的变化率,也即期权理论价值对标的资产价格的二阶导数, Γ = ∂ Δ ∂ S = ∂ 2 V ∂ S 2 \Gamma = \frac{\partial \Delta}{\partial S} = \frac{\partial ^{2} V}{\partial S^{2}} Γ=∂S∂Δ=∂S2∂2V。
基于BS Model,欧式期权,无分红下Delta的计算公式为:
Γ = ϕ ( d 1 ) S σ τ \Gamma = \frac{\phi(d_{1})}{S\sigma\sqrt{\tau }} Γ=Sστϕ(d1)
其中,
- ϕ \phi ϕ是标准正态分布的概率密度函数, ϕ ( x ) = e − x 2 2 2 π \phi(x) = \frac{e^{-\frac{x^{2}}{2}}}{\sqrt{2\pi}} ϕ(x)=2πe−2x2;
意义与用法
绝大多数的期权多头拥有正的Gamma,平值期权的Gamma最大,而深实值或深虚值期权的Gamma则趋近于0。随着到期日的临近,平值期权的Gamma还会急剧增加。
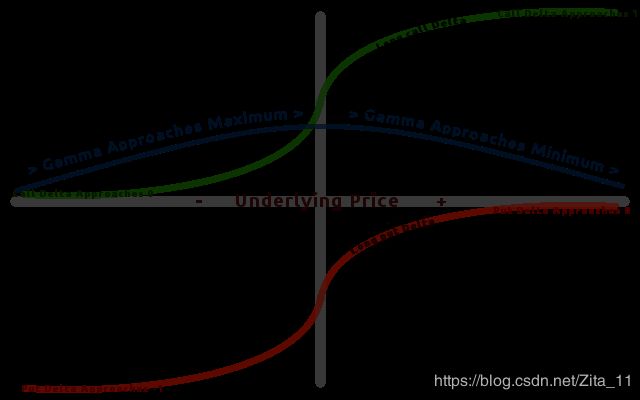
Gamma常被用于衡量对冲风险。当标的价格变化一个单位时,为了保证对冲的效果,需要调整对冲比率Delta,而新的Delta值便等于原来的Delta值加上(减去)Gamma值。因此Gamma值越大,Delta值变化越快,进行Delta中性对冲时的风险程度也越高。
3. Vega
定义与计算
Vega衡量期权理论价值相对于标的资产隐含(预期)波动率的变化率, ν = ∂ V ∂ σ \nu =\frac{\partial V}{\partial \sigma} ν=∂σ∂V。
基于BS Model,欧式期权,无分红下Delta的计算公式为:
ν = S ϕ ( d 1 ) τ \nu = S\phi (d_{1})\sqrt{\tau } ν=Sϕ(d1)τ
- 业内习惯把Vega理解为波动率变动1个百分点对应期权价值的变化量,所以根据此公式计算出的vega还需再除以100。
意义与用法
期权价格随着标的资产预期波动率的增加而上升,因此不论认购还是认沽,多头期权的Vega都是正数,空头期权的Vega都是负数。平值期权的Vega值最大,当期权处于较深的价内或价外时,Vega值接近于0。
4. Theta
定义与计算
Theta衡量期权时间价值的损耗,表示时间每经过一天,期权价值会损失多少, Θ = − ∂ V ∂ τ \Theta=-\frac{\partial V}{\partial \tau} Θ=−∂τ∂V。
基于BS Model,欧式期权,无分红下Theta的计算公式为:
| Call | Put |
|---|---|
| Θ = − S ϕ ( d 1 ) σ 2 τ − r K e − r τ Φ ( d 2 ) \Theta = -\frac{S\phi(d_{1})\sigma}{2\sqrt{\tau }} - rKe^{-r\tau }\Phi(d_{2}) Θ=−2τSϕ(d1)σ−rKe−rτΦ(d2) | Θ = − S ϕ ( d 1 ) σ 2 τ + r K e − r τ Φ ( − d 2 ) \Theta = -\frac{S\phi(d_{1})\sigma}{2\sqrt{\tau }} + rKe^{-r\tau }\Phi(-d_{2}) Θ=−2τSϕ(d1)σ+rKe−rτΦ(−d2) |
- d 2 = l n ( S / K ) + ( r − σ 2 / 2 ) τ σ τ = d 1 − σ τ d_{2} = \frac{ln(S/K) + (r - {\sigma ^{2}}/2)\tau }{ \sigma\sqrt{\tau } }=d_{1} - \sigma\sqrt{\tau} d2=στln(S/K)+(r−σ2/2)τ=d1−στ
- 业内习惯Theta用来衡量每日的time decay,而BS Model中的时间单位是年,所以按此公式算出来的Theta需要再除以365。
意义与用法
不论是看涨还是看跌期权,随着时间的流逝,期权价值都会不断下降,所以对于期权多头,Theta值几乎都为负,而对于期权空头,则每天都在坐享时间价值的收入。一个例外是深度实值的欧式认沽期权,其Theta值可能为正。越接近到期日,期权的时间价值消逝的速度会越快,即Theta的绝对值会随时间消逝而变大。
5. Python实现
import numpy as np
import scipy.stats as si
def d(s,k,r,T,sigma):
d1 = (np.log(s / k) + (r + 0.5 * sigma ** 2) * T) / (sigma * np.sqrt(T))
d2 = d1 - sigma * np.sqrt(T)
return (d1,d2)
def delta(s,k,r,T,sigma,n):
'''
认购期权的n为1
认沽期权的n为-1
'''
d1 = d(s,k,r,T,sigma)[0]
delta = n * si.norm.cdf(n * d1)
return delta
def gamma(s,k,r,T,sigma):
d1 = d(s,k,r,T,sigma)[0]
gamma = si.norm.pdf(d1) / (s * sigma * np.sqrt(T))
return gamma
def vega(s,k,r,T,sigma):
d1 = d(s,k,r,T,sigma)[0]
vega = (s * si.norm.pdf(d1) * np.sqrt(T)) / 100
return vega
def theta(s,k,r,T,sigma,n):
'''
认购期权的n为1
认沽期权的n为-1
'''
d1 = d(s,k,r,T,sigma)[0]
d2 = d(s,k,r,T,sigma)[1]
theta = (-1 * (s * si.norm.pdf(d1) * sigma) / (2 * np.sqrt(T)) - n * r * k * np.exp(-r * T) * si.norm.cdf(n * d2)) / 365
return theta
最后计算出的Greeks值,可以对照Options Calculator来查验纠错。
参考
WIKIPEDIA: Greeks
Investopedia: Greeks
知乎:期权之希腊字母Delta, Gamma, Vega和Theta解读