2019年9月8日秋季PAT甲级题解-4 Dijkstra Sequence (30 分) 详细分析

Dijkstra's algorithm is one of the very famous greedy algorithms. It is used for solving the single source shortest path problem which gives the shortest paths from one particular source vertex to all the other vertices of the given graph. It was conceived by computer scientist Edsger W. Dijkstra in 1956 and published three years later.

In this algorithm, a set contains vertices included in shortest path tree is maintained. During each step, we find one vertex which is not yet included and has a minimum distance from the source, and collect it into the set. Hence step by step an ordered sequence of vertices, let's call it Dijkstra sequence, is generated by Dijkstra's algorithm.

On the other hand, for a given graph, there could be more than one Dijkstra sequence. For example, both { 5, 1, 3, 4, 2 } and { 5, 3, 1, 2, 4 } are Dijkstra sequences for the graph, where 5 is the source. Your job is to check whether a given sequence is Dijkstra sequence or not.

Input Specification:

Each input file contains one test case. For each case, the first line contains two positive integers N​v​​ (≤10​^3​​) and N​e​​ (≤10^​5​​), which are the total numbers of vertices and edges, respectively. Hence the vertices are numbered from 1 to N​v​​.

Then N​e​​ lines follow, each describes an edge by giving the indices of the vertices at the two ends, followed by a positive integer weight (≤100) of the edge. It is guaranteed that the given graph is connected.

Finally the number of queries, K, is given as a positive integer no larger than 100, followed by K lines of sequences, each contains a permutationof the N​v​​ vertices. It is assumed that the first vertex is the source for each sequence.

All the inputs in a line are separated by a space.

Output Specification:

For each of the K sequences, print in a line Yes if it is a Dijkstra sequence, or No if not.

Sample Input:

5 7
1 2 2
1 5 1
2 3 1
2 4 1
2 5 2
3 5 1
3 4 1
4
5 1 3 4 2
5 3 1 2 4
2 3 4 5 1
3 2 1 5 4

Sample Output:

Yes
Yes
Yes
No

题意

给出一个无向图和一些序列，判断这些序列是否有dijkstra算法产生的合法序列（就是按照dijkstra算法遍历图的顺序）。

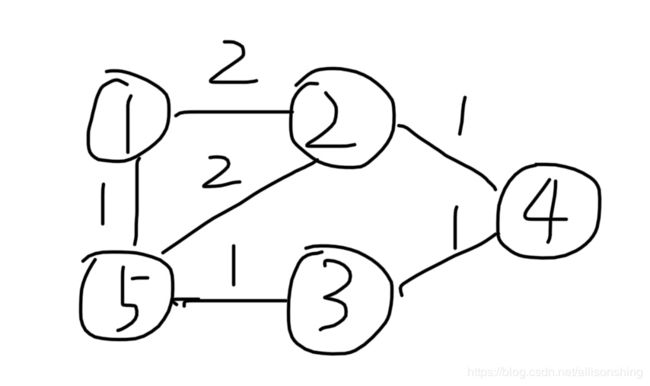
做出上述测试的无向图：

分析

这道题不是“常规的Dijkstra的题（也就是像1087那种套个模板就行的）”，但是不用恐惧，只要仔细分析一下：

题目给的输入的最后一个序列 3 2 1 5 4为什么不行呢？

因为在第3个数（即1）的时候，起点3到点1的距离d[1]为3（点3->点2->点1），但是最短路径为1（点3->点4）.

也就是说给出的序列是Dijkstra序列的关键在于，序列的第i个数x的d[x]是等于当时求到的最短路径。

如果是的话，在后面的一步就要以x为u来松弛了。

与题目同样的图例，我再写三个非常相似的输入用例：

5 7
1 2 2
1 5 1
2 3 1
2 4 1
2 5 2
3 5 1
3 4 1
3
3 2 5 4 1
3 2 5 1 4
3 2 1 5 4
正确代码的测试输出是：
s[i] u minn d[s[i]]
  3  3   0   0
  2  2   1   1
  5  4   1   1
  4  4   1   1
  1  1   2   2
Yes
s[i] u minn d[s[i]]
  3  3   0   0
  2  2   1   1
  5  4   1   1
  1  4   1   2
No
s[i] u minn d[s[i]]
  3  3   0   0
  2  2   1   1
  1  4   1   3
No

 

满分代码

//得分30,满分30
#include
using namespace std;
const int INF=0x3f3f3f3f;
const int maxn=1005;
int d[maxn],s[maxn],G[maxn][maxn];
bool visit[maxn];
int main(){
    int n,m,a,b,c,k;
    scanf("%d %d\n",&n,&m);
    fill(G[0],G[0]+maxn*maxn,INF);
    while(m--){
        scanf("%d %d %d\n",&a,&b,&c);
        G[a][b]=G[b][a]=c;
    }
    scanf("%d\n",&k);
    while(k--){
        m=n;
        for(int i=1;i<=n;i++){
            scanf("%d",&s[i]);
        }
        bool f=true;
        int start=s[1];
        fill(visit,visit+maxn,false);
        fill(d,d+maxn,INF);
        d[start]=0;
        for(int i=1;i<=n;i++){
            int u = -1, minn = INF;
            for (int j = 1; j <= n; j++) {
                if (!visit[j] && d[j] < minn) {
                    u = j;
                    minn = d[j];
                }
            }
            if (u == -1 || d[u] != d[s[i]]){
                f=false;
                continue;
            }
            u = s[i];
            visit[u]=true;
            for(int v=1;v<=n;v++){
                if(!visit[v] && G[u][v]!=INF && G[u][v]+d[u]

备考汇总贴：2020年6月PAT甲级满分必备刷题技巧

如果喜欢我的博客，请为我点个赞，也欢迎多评论、转发，感谢！！