数论初步(欧几里得算法&求解模线性方程&求解模线性方程组&求逆元)
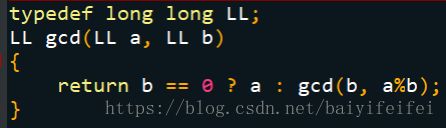
最大公约数的辗转相除法(欧几里得算法)证明:
给出两个数a和b,求其最大公约数。
设a%b=y;
则a=k*b+y(k为一整数)
设a,b的最小公约数为u
则:
- (k*b+y)%u=0;
- b%u=0;
由(2)式可知k*b%u=0,所以y%u=0
所以a,b的最小公约数就可以转换为b,y的最小公约数。
因此就可以通过不断递归,向下进行计算
直到a%b=0时,就有b为最大公倍数。
贝祖定理:ax+by=gcd(a,b).
扩展欧几里得算法:
通过欧几里得算法
我们知道最终的a,b与gcd的关系式为
a*1+b*0=gcd。
但是我们要如何求出一开始的ax+by=gcd的x与y呢?
由欧几里得算法可知a,b的最大公约数和b,a%b的最大公约数相等,因此有下式
b*x1+(a%b)*y1=gcd;
而a%b=a-(a/b)*b(式子中的除为整除)
因此原式可以转化为:
b*x1+(a-(a/b)*b)*y1=gcd;
经过变形就可以得到:
a*y1+b*(x1-(a/b)*y1)=gcd;
所以x=y1,y=x1-(a/b)*y1.
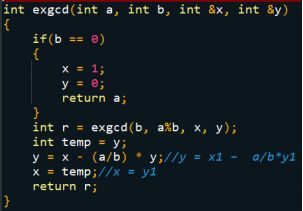
由此得扩展欧几里得算法:
a|b<==>b%a=0
a≡b(mod n)意为a与b同余,即a%n=b%n
求解模线性方程:
模线性方程即为ax≡b(mod n)对x进行求解。
根据同模的性质我们不难将原模线性方程ax≡b(mod n)转换为
ax%n=b%n;
并令其余数均为q则有ax%n=b%n=q;
再令存在整数k1,k2使得
(1)ax=k1*n+q;
(2)b=k2*n+q;
进而对(1)(2)两式进行作差,则得到下式:
ax-b=n*(k1-k2);
移项后得到:
ax-n(k1-k2)=b;
再令-(k1-k2)为y,进一步对原式进行转化,则可得
ax+ny=b;
不难发现此式与贝祖定理的形式相同。因此若想方程有解则需满足
gcd(a,n)|b
那么方程的解:
令gcd(a,n)=d;假定方程有解(d|b)x0为方程的任意一个解,则方程该方程对模a有d个解,xi=x0+i*(n/d)(i=1,2,3,......d-1)
证明:
因为x0是方程的一个解所以有ax0≡b(mod n)
进而我们再将xi带入这个方程则有:
a(x0+i*(n/d))=ax0+i*n*(a/d)
由于d是a的约数所以a/d=为一个整数,所以axi%n=ax0%n
得证。
求解模线性方程组:
分别给出n个mi和bi
他们共同构成这样一个方程组:
(1)X%m1=b1;
(2)X%m2=b2;
.............
(i)X%mi=bi;
..............
(n)X%mn=bn.
要求我们对它进行求解。
首先我们对(1)(2)式子进行联立求解:
先将原方程转换为
x=k1*m1+b1
X=k2*m2+b2
对两式作差得到k1*m1-k2*m2=b2-b1;(E)
通过扩展欧几里得求得k1,k2
将k1代入原方程,得到x0=k1*m1+b1。
再回到方程E,原方程可以化作
m1*k1-m2*k2+s*m1*m2-s*m1*m2=b2-b1;(s为任意整数)
再对原式进行化简:
m1*(k1-sm2)+m2*(k2+s*m1)=b2-b1;
由此可得x=(k1-sm2)*m1+b1=k1*m1+b1-s*m1*m2
由于x0=k1*m1+b1
所以我们可以进一步得到
X=x0+s*m1*m2
这个方程也就可以进一步转化为:
X%(m2*m2)=x0
可以进一步转化为
X%(lcm(m1,m2))=x0;
得到这个式子之后再继续和别的式子进行联立即可,最终只剩下一个方程后再用求解模线性方程的方式求解即可。
逆元:
方程ax≡1(mod p),的解x称为a关于模p的逆,当g c d(a , p)==1(即a,p互质)时,方程有唯一解,否则无解。
证明:
上面已经证明过了一个模线性方程只有当b|d时有解且解的个数为d(d为gcd(a,p))由于在逆元的求解中b为1所以只有1可以被它整除,所以只有此时有唯一解。
性质:对于一些题目会要求把结果模一个数,通常是一个较大的质数,对于加减乘法通过同余定理可以直接拆开计算,但对于(a/b)%m这个式子,是不可以写成(a%m/b%m)%m的,但是可以写为(a*b-1)%m,其中b-1表示b的逆元
费马小定理:
假如p是质数,且gcd(a,p)=1,那么有
a^(p-1) ≡ 1(mod p)
证明:
任意取一个质数,比如13。考虑从1到12的一系列整数1,2,3,4,5,6,7,8,9,10,11,12,给这些数都乘上一个与13互质的数,比如3,得到3,6,9,12,15,18,21,24,27,30,33,36。对于模13来说,这些数同余于3,6,9,12,2,5,8,11,1,4,7,10。这些余数实际上就是原来的1,2,3,4,5,6,7,8,9,10,11,12,只是顺序不同而已。
把1,2,3,„,12统统乘起来,乘积就是12的阶乘12!。把3,6,9,„,36也统统乘起来,并且提出公因子3,乘积就是312×12!。对于模13来说,这两个乘积都同余于1,2,3,„,12系列,尽管顺序不是一一对应,即312×12!≡12!mod 13。两边同时除以12!得312≡1 mod 13。如果用p代替13,用x代替3,就得到费马小定理
xp-1≡1 mod p。
应用:
原式可以化成a*(a^(p-2))≡1(mod p)
所以a^(p-2)就是a关于模p的逆元
欧几里得求逆元:
用欧几里得对ax≡1(mod p)求解,上面以写出求解方式,求出的解就是逆元