一个借鉴现代OS的MMU的排序算法

很久很久以前，我写过两篇文章，关于一个突然想出来的点子整合出来的一个排序算法：
移位排序算法–从赛跑想到的：http://blog.csdn.net/dog250/article/details/5303538
一个快得出奇又慢得可以的比特排序算法：http://blog.csdn.net/dog250/article/details/6817795
后来发现这个排序算法其实就是Radix基排序或者说是基排和桶排的结合吧，当时不知道，现在肯定是知道了。在第二篇文章里我还写了3种实现，想想看那时也是够拼的了，我这种不会编程的人原来偶尔也是会写点代码的。
…
  一晃就是7年过去了，周四下午快下班的时候，一个技术讨论群里放出了一个问题，不知怎地就让我关联到了排序问题(关于这个背景我在文章的附录详述)，我便花了10分钟随便码了几行代码，虽然很是感兴趣，但由于马上就下班了，我也不想为了这种与工作无关的问题加班，所以就走了，但是上地铁排队时，突然想到点什么，就特别想coding，然而却没有带电脑！怎么办？

  我想到了手机云编译，于是就下载了一个手机上的编译器，在地铁上尽情地装逼起来。幸亏我把那几行代码发到了群里，这才能在路上下载下来重新在手机上编辑编译…

  差点就坐过了站，马上就要下车时，代码终于有了结果，编译通过，结果正确，也很是激动，还发了朋友圈，很多人点了赞(其实要是能点“没有帮助”，估计会更多)。不管怎样，我觉得至少可以随时随地编程(我也不会随时随地编程，我根本就不会编程)了。

  我还原一下当时的场景：

---

好了，回归排序问题。

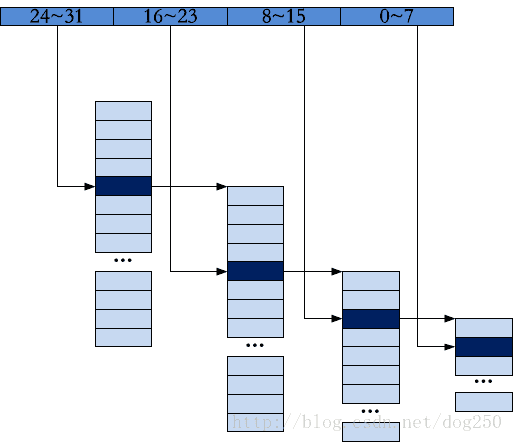
  我的思路很简单，空间换时间是根本。而且我知道，越是规则的空间越是能节省大量的时间，于是我学习OS内核MMU实现的样子，实现了一个排序版本，自认为要比我在2011年实现的那版要好一点。

  以32位数字的排序为例，我把每一个数字分为4个8位，每一组8位组分别排序：

这就是一个256叉树，而排序过程就是一个将一个个数字不断插入到这个256叉树的过程，而这很容易，只需要4次定位即可，每一个8位组都有256个桶，一个8位组比如说其值是n(0到255)，那就将其放入第n个桶呗。

  如果你对此不解，很容易，考虑以下问题：你的内存无限大前提下，排序算法的时间复杂度是多少？很简单嘛， O(1) ，为什么呢？因为时空等价性，空间无穷，时间就恒定，反过来时间无穷，空间就恒定。

  你只需顺序排列无穷多个桶，把数字n放到第n个桶里，然后顺序把非空的桶撸一遍即可。但现实肯定不可能是内存无限大，那么势必要有所取舍！

  我们把一个平坦的空间进行折叠，就成了类似MMU三级页表的样子，但是你会发现，如果是寻址到每一个地址而不是每一个页面(一般而言，4096个地址就是一个页面，别较真儿扯什么大页，这个我懂)，寻址完整个4G的空间需要的页目录和页表项，其实是一个字节都少不了，还会增加基础设施的开销，如果你的内存只有4G，那么光页表就要占完了，不信你算算看。

  但是为什么我们可以用3级页表来进行MMU的实现呢？30年经久不衰的机制，到底妙义何在？首先我们寻址是按页面来的，而不是按地址来的。其次，OS进程的地址都是有聚集性的，也就是说一个进程内的地址都是密集聚合的，而不是稀疏分布的，以4位地址举例，更可能的情况是，1,2,3,4,5,9,10,11,12,13，而不会是1,3,5,7,9,11,13,15。所以OS内核的MMU一直以这种方式实现而没有被淘汰，是有理由的。

  因此，如果有的数组符合进程地址的局部性分布特征，那么自然就可以用这种OS经久不衰的方式进行数据排序了。

  说白了，就是如果数组的元素分布是密集的而不是稀疏的话，就可以采用MMU的方式进行排序了，如果待排序数组是稀疏的，那么显然需要比较多的内存了，此时就需要权衡用空间换时间是不是划算了。不管怎么说，我下班前以及在路上实现了一个简版，代码如下：

#include 
#include 
#include 

struct entry {
        struct entry *p;
        int inuse;
        char value;
};

struct entry base[256];

void insert(int value)
{
        unsigned char a1, a2, a3, a4;
        struct entry *ent2, *ent3, *ent4;

        a1 = (value&0xff000000)>>24;
        a2 = (value&0x00ff0000)>>16;
        a3 = (value&0x0000ff00)>>8;
        a4 = (value&0x000000ff);

        base[a1].value = a1;
        base[a1].inuse = 1;
        if (base[a1].p == NULL) {
                base[a1].p = (struct entry*)calloc(1, 256*sizeof(struct entry));
        } 

        ent2 = base[a1].p + a2;
        ent2->value = a2;
        ent2->inuse = 1;
        if (ent2->p == NULL) {
                ent2->p = (struct entry*)calloc(1, 256*sizeof(struct entry));
        } 

        ent3 = ent2->p + a3;
        ent3->value = a3;
        ent3->inuse = 1;
        if (ent3->p == NULL) {
                ent3->p = (struct entry*)calloc(1, 256*sizeof(struct entry));
        } 

        ent4 = ent3->p + a4;
        ent4->value = a4;
        ent4->inuse = 1;
}

void print_result()
{
        int i = 0, j, k, l;
        unsigned char a4, a3, a2, a1;
        struct entry *l0 = base;
        for (i = 0; i < 256; i++) {
                if (l0[i].inuse) {
                        a1 = l0[i].value & 0xff;
                        struct entry *l1 = l0[i].p;
                        for (j = 0; j < 256; j++) {
                                if (l1[j].inuse) {
                                        a2 = l1[j].value & 0xff;
                                        struct entry *l2 = l1[j].p;
                                        for (k = 0; k < 256; k++) {
                                                if (l2[k].inuse) {
                                                        a3 = l2[k].value & 0xff;
                                                        struct entry *l3 = l2[k].p;
                                                        for (l = 0; l < 256; l++) {
                                                                if (l3[l].inuse) {
                                                                        int d;
                                                                        a4 = l3[l].value & 0xff;
                                                                        d = (a1<<24|a2<<16|a3<<8|a4);
                                                                        printf("%u \n", d);

                                                                }
                                                        }
                                                }
                                        }

                                }
                        }
                }
        }
}

int main(int argc, char **argv)
{
        int value = 0;
        memset(base, 0, 256*sizeof(struct entry));

        int i = 0;

        for (i = 0; i < 100; i++) {
                int v = random()&0xffffffff;
                insert(v);
                printf("%d \n", v);
        }
        printf("--------------------\n");
        print_result();
        printf("\n");
}

好了，如果随机序列生成的好足够密集，这就是空间换时间，你能期望它的运行时间有一个好的成绩，如果比较稀疏，那么至少它还能正确运行。美中不足是最终取排序好的数据时那个256叉树的前序遍历或者说是深度优先遍历的不雅操作。以下是100个数字的排序运行结果：

1804289383 
846930886 
1681692777 
1714636915 
1957747793 
424238335 
719885386 
1649760492 
596516649 
1189641421 
1025202362 
1350490027 
783368690 
1102520059 
2044897763 
1967513926 
1365180540 
1540383426 
304089172 
1303455736 
35005211 
521595368 
294702567 
1726956429 
336465782 
861021530 
278722862 
233665123 
2145174067 
468703135 
1101513929 
1801979802 
1315634022 
635723058 
1369133069 
1125898167 
1059961393 
2089018456 
628175011 
1656478042 
1131176229 
1653377373 
859484421 
1914544919 
608413784 
756898537 
1734575198 
1973594324 
149798315 
2038664370 
1129566413 
184803526 
412776091 
1424268980 
1911759956 
749241873 
137806862 
42999170 
982906996 
135497281 
511702305 
2084420925 
1937477084 
1827336327 
572660336 
1159126505 
805750846 
1632621729 
1100661313 
1433925857 
1141616124 
84353895 
939819582 
2001100545 
1998898814 
1548233367 
610515434 
1585990364 
1374344043 
760313750 
1477171087 
356426808 
945117276 
1889947178 
1780695788 
709393584 
491705403 
1918502651 
752392754 
1474612399 
2053999932 
1264095060 
1411549676 
1843993368 
943947739 
1984210012 
855636226 
1749698586 
1469348094 
1956297539 
--------------------
35005211 
42999170 
84353895 
135497281 
137806862 
149798315 
184803526 
233665123 
278722862 
294702567 
304089172 
336465782 
356426808 
412776091 
424238335 
468703135 
491705403 
511702305 
521595368 
572660336 
596516649 
608413784 
610515434 
628175011 
635723058 
709393584 
719885386 
749241873 
752392754 
756898537 
760313750 
783368690 
805750846 
846930886 
855636226 
859484421 
861021530 
939819582 
943947739 
945117276 
982906996 
1025202362 
1059961393 
1100661313 
1101513929 
1102520059 
1125898167 
1129566413 
1131176229 
1141616124 
1159126505 
1189641421 
1264095060 
1303455736 
1315634022 
1350490027 
1365180540 
1369133069 
1374344043 
1411549676 
1424268980 
1433925857 
1469348094 
1474612399 
1477171087 
1540383426 
1548233367 
1585990364 
1632621729 
1649760492 
1653377373 
1656478042 
1681692777 
1714636915 
1726956429 
1734575198 
1749698586 
1780695788 
1801979802 
1804289383 
1827336327 
1843993368 
1889947178 
1911759956 
1914544919 
1918502651 
1937477084 
1956297539 
1957747793 
1967513926 
1973594324 
1984210012 
1998898814 
2001100545 
2038664370 
2044897763 
2053999932 
2084420925 
2089018456 
2145174067

求助：取结果就是一个256叉树的深度优先遍历，有什么好办法呢？

---

我为什么过了7年还这么钟情于这个算法，哦，不，应该是更久。这是为什么？
因为我钟情于定位而不是查找。我比较喜欢的东西都是类似的，比如我喜欢Linux内核中的Trie路由查找算法而不是Hash路由查找算法，比如我喜欢DxR，我喜欢Radix树，我喜欢MMU，我喜欢TCAM…我还自己设计了DxRPro以及DxRPro++…所有这些几乎都是一类东西，且这些都属于定位结构而不是查找算法。

  这些都是形而上的东西，没法给人以指导，但事实上这对于我来讲至少在技术上是最重要的东西。

—————-附录：起因—————-
当我在review那个Linux 4.15关于TCP重传队列重构成红黑树的patch时，一个技术讨论群里在讨论红黑树和链表的区别的问题。大致是在问它们之间的边界在哪里。想到正好在看和这个相关的东西，我就在群里说了几句，大致说了：

1. 你回答的时候就告诉他把一个entry同时链在一个链表和一棵红黑树是一个绝妙的主意，既可以遍历，又方便查找；
2. 你就告诉他链表是用来做户口普查的，红黑树是用来抓人的，两个都需要，你自己不同时有户口本和身份证吗？
3. 举一个技术上例子比什么都强，Linux内核中的vma就是这么组织的，一个vma同时在一个链表和一棵树中；
4. 还是不解？比如说查找特定vma时就需要红黑树结构，比如想销毁一切vma时就需要从链表上来遍历所有的节点。
   …

然后，想象了一下红黑树的序列化结构，如果有可能，一棵标准的完全二叉树是梦寐以求的，然而在现实世界中，万事讲权衡，于是就有了AVL树，红黑树这般，不管哪类树，区别仅仅在于约束不同，其序列是完全一致的，这不禁就让我想起来构成这个序列的排序算法，我希望找一种与众不同的算法，于是就想到很久之前的赛跑算法，优化之，成此文。

PS：我觉得算法要比编程语言更重要，真是这样的。语言只需要精通一种，其余的会即可，但是算法却只有一个。 为什么很多屡次都不能明白这一点！？！