mahout学习之聚类(1)——向量的引入与距离测度
聚类的基本概念
聚类就是将一个给定的文档集中的相似项目分成不同簇的过程,可以将簇看作一组簇内相似而簇间有别的项目的集合。
对文档集的聚类涉及以下三件事:
1. 一个算法:将文档集阻止到一起的算法
2. 相似性与不相似的概念
3. 停止的条件
聚类数据的表示
mahout将输入数据以向量的形式保存,在机器学习领域,向量指一个有序的数列,有多个维度,每个维度都有一个值。比如在二维空间,一个坐标就是一个向量。
将数据转换为向量
在mahout中,向量被实现为三个不同的类来针对不同的场景:
1. DenseVector:可以视为一个double型的数组,不管向量是否为0,都会分配空间,被称为密集型的。
2. RandomAccessSparseVector:可以视为一个HashMap(Integer,Double),只为非0元素分配空间,被称为稀疏向量。
3. SequentialAccessSparseVector:实现为两个并列的数组,一个Integer,一个Double,相比于面向随机访问的randomAccessSparseVector,这个更适合顺序读取。
假设有一堆苹果,用形状,大小,颜色作为三个维度来聚类,那么重量可以简单的用克或者千克来测量,大小可以定义小苹果为1,中苹果为2,大苹果为3,颜色可以采取该颜色的波长来表示(400~650nm),这样三个维度就都是一个有意义且客观的维度值,一堆苹果的向量如下:
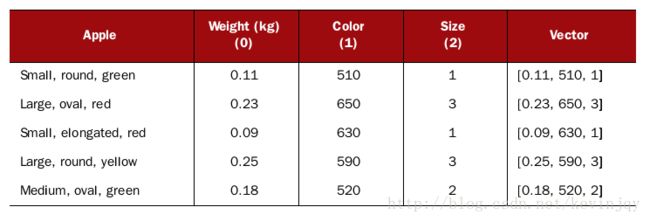
其实有一个问题,那就是颜色的差异在距离测度上大于其他两者,可以通过加权来解决这个问题。
以下为一个为各种苹果生成向量的示例代码:
public static void main(String args[]) throws Exception {
List apples = new ArrayList();
NamedVector apple;
//将名字与向量相关联
apple = new NamedVector(
new DenseVector(new double[] {0.11, 510, 1}),
"Small round green apple");
apples.add(apple);
apple = new NamedVector(
new DenseVector(new double[] {0.23, 650, 3}),
"Large oval red apple");
apples.add(apple);
apple = new NamedVector(
new DenseVector(new double[] {0.09, 630, 1}),
"Small elongated red apple");
apples.add(apple);
apple = new NamedVector(
new DenseVector(new double[] {0.25, 590, 3}),
"Large round yellow apple");
apples.add(apple);
apple = new NamedVector(
new DenseVector(new double[] {0.18, 520, 2}),
"Medium oval green apple");
Configuration conf = new Configuration();
FileSystem fs = FileSystem.get(conf);
Path path = new Path("appledata/apples");
////SequenceFile是为hadoop中的一种文件格式,以一个键值对序列组成
//键必须为WritableComparable,值必须实现为Writable。类似java中的comparable和serializable
SequenceFile.Writer writer = new SequenceFile.Writer(fs, conf,
path, Text.class, VectorWritable.class);
//序列化向量数据
VectorWritable vec = new VectorWritable();
for (NamedVector vector : apples) {
vec.set(vector);
writer.append(new Text(vector.getName()), vec);
}
writer.close();
SequenceFile.Reader reader = new SequenceFile.Reader(fs,
new Path("appledata/apples"), conf);
Text key = new Text();
//反序列化向量数据
VectorWritable value = new VectorWritable();
while (reader.next(key, value)) {
System.out.println(key.toString() + " "
+ value.get().asFormatString());
}
reader.close();
} 将文本文档表示为向量
VSM(Vector Space Model)是向量化文本文档的常见方法,假设一个包含了所有文档中出现的单词的集合,其中的每个单词至少出现过一次,假定每个单词被分配一个编号,那么这个编号就是文档向量拥有的维度。这种方法导致的结果就是文档向量的维度会非常大,最坏情况是拥有多少个单词就有多少维度。
对于一个单词而言,向量维度上的值通常就是词频(TF),也被称为权重,有一些单词经常出现,比如a,an,the等等,被称为停用词,这些单词出现次数多而对于判断文档是否相似并没有帮助。
TF-IDF改进加权
TF-IDF(词频-逆文档频率)用来改进词频加权,而不是简单的使用词频作为权重。
假设一篇文档中单词w1,w2,w3,w4…的频率为f1,f2,f3,f4….
定义文档频率DF = 有这个单词出现的文档个数,而不是在文档中出现的次数。那么单词w的

如果一个单词在文档中频繁出现,那IDF的值就会很小,这不合适,所以一般乘以文档个数n:

所以,在文档向量中单词w的权重W为:

上述的IDF值仍然很不理想,因为它掩盖了最终的单词权重中TF的影响。未来解决这个问题,通常使用IDF的对数:
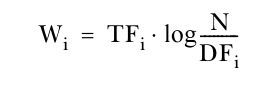
这就是经典的TF-IDF值。不过VSM假设所有单词作为维度都是相互正交的,即相互没有关系的,这明显有问题,比如聚类和算法两个词同时出现的可能性就很大。未来解决单词的相互依赖问题,mahout提供了一种被称为搭配的方法。
通过n-gram搭配词考察单词的依赖性
一组单词被称为一个n-gram(或者biggram),比如php is the best language就是一个5-gram,这样的话,就不必把维度映射到单个单词,可以映射到一组单词,当然也可以两种方式搭配使用。比如句子 “It was the best of times, it was the worst of times,” 可以产生如下的biggram:
It was
was the
the best
best of
of times
times it
it was
was the
the worst
worst of
of times
有些很有用处,比如it was,the best,但是也有些没有用的,比如was the ,这样会对结果造成干扰,好在mahout利用一种对数似然的方法判断两个词出现在一起是偶然的还是因为形成了一个有意义的单元,这样就可以排除掉无意义的。
mahout中, DictionaryVectorizer 类将文本文档通过TF-IDF加权和n-gram搭配来将词转化为向量。
基于归一化改善向量的质量
归一化是一个清理边界情况的过程,带有异常特征的数据会导致结果出现不正常的偏差。比如一个大文档因为有很多非0的维度会导致和很多小文档相似,所以在计算相似性的时候需要抵消向量大小不同造成的影响,降低大向量的影响并且提升小向量的影响的过程被称为归一化。
在mahout中,归一化使用了统计学中的p范数,例如一个三维向量的p范数为:
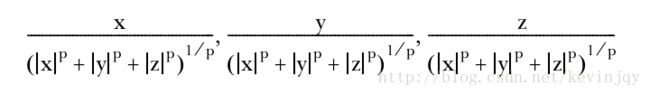
表达式![]() 可视为一个向量的范数,让每个向量的值都除以这个数字。
可视为一个向量的范数,让每个向量的值都除以这个数字。
向量的一范数或者曼哈顿范数就是p=1的情况,p可以是大于0的任意值。
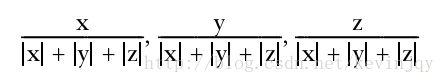
二范数或者欧式范数:

无穷范数简单的将向量除以最大幅值维度的权重:
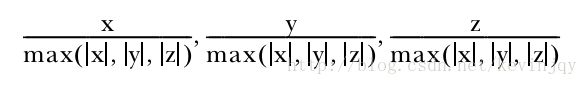
选择的p值取决于对该向量采取哪种距离测度,如果是曼哈顿距离测度,那就用一范数,其他同理。
项目相似性的度量
欧式距离测度
欧式距离很简单,假设两个n维向量:(a1,a2,,,,an),(b1,b2,,,bn)。那么它们之间的欧式距离表示为:
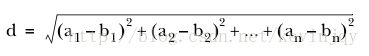
Mahout实现这个度量的类为: EuclideanDistanceMeasure.。
平方欧式距离测度
正如名称所示,值是欧式距离的平方。
![]()
Mahout实现这个度量的类为:SquaredEuclideanDistanceMeasure。
曼哈顿距离测度
不同于前两者,曼哈顿距离为两个点坐标差的绝对值之和,曼哈顿距离表示为:
![]()
直观一点:
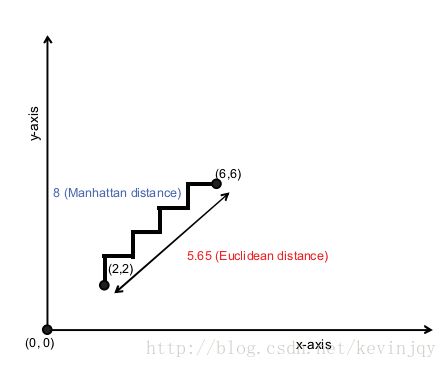
Mahout实现这个度量的类为: ManhattanDistanceMeasure.
余弦距离测度
坐标与原点形成一条向量,坐标之间的夹角即为余弦距离测度:

直观一点:
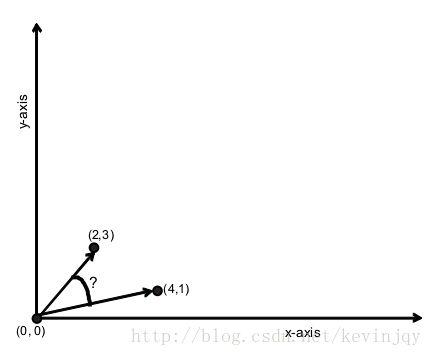
值得注意的一点是,这种测度方式不关心长度,只关心方向,测度的范围从0.0(方向相同)到2.0(方向相反)。
Mahout实现这个度量的类为: CosineDistanceMeasure.
谷本距离测度
加入有三个点(1.0,1.0)(3.5,3.5)(2.6,2.6)。那余弦距离毫无用处,因为方向相同,使用欧式距离可以起效,但是它忽视了方向相同的事实。谷本距离可以同时表现距离和夹角。公式为:
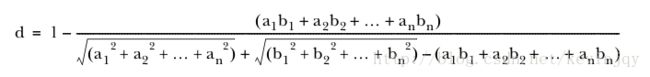
Mahout实现这个度量的类为:TanimotoDistanceMeasure.
加权距离测度
mahout还提供了一个基于欧式距离或者曼哈顿距离的测度实现,WeightedDistanceMeasure类。它允许对不同维度加权从而提高或者减少某些维度对于结果的影响,权重需要以vector的形式序列化到一个文件中。