R语言处理时间序列数据
R语言处理时间序列数据
根据时间序列数据对未来值进行预测是人类的基本活动,如城市规划者基于时序数据预测未来的交通需求,气候学家尝试通过时序数据预测全球气候变化,医疗保健人员根据时序数据研究疾病的传播范围及某区域内可能出现的病例数,地震学家通过时序数据预测地震……
1. 生成时序对象
在R中分析时间序列的前提是将分析对象转换成时间序列对象(time-series object),该对象包含了观测值、起始时间、终止时间以及周期(如月、季度、年)的结构。利用ts()函数可对传统数据转换为时间序列数据
#生成时序对象(generate time-series object)
> sales <- c(18,33,41,7,34,3,24,25,24,21,25,20,22,31,40,29,25,21,22,54,31,25,26,35)
> tsales <- ts(sales,start = c(2003,1),frequency = 12)
> tsales
Jan Feb Mar Apr May Jun Jul Aug Sep Oct Nov Dec
2003 18 33 41 7 34 3 24 25 24 21 25 20
2004 22 31 40 29 25 21 22 54 31 25 26 35
> start(tsales)
[1] 2003 1
> end(tsales)
[1] 2004 12
> frequency(tsales)
[1] 12
> plot(tsales,pch=19)
> #提取子集(extract the subject)
> tsales.subject <- window(tsales,start=c(2003,5),end=c(2004,6))
> tsales.subject
Jan Feb Mar Apr May Jun Jul Aug Sep Oct Nov Dec
2003 34 3 24 25 24 21 25 20
2004 22 31 40 29 25 21
- 时序的平滑化和季节性分解
通过对数据平滑化处理能够了解数据的时序变化趋势,以下代码为通过简单移动平均的方法进行平滑处理,以及平滑后的图
>#install.packages("forecast")
> libray(forecast)
> opar <- par(no.readonly = TRUE) #添加参数no.readonly=TRUE可以生成一个可以修改的当前图形参数列表
> par(mfrow=c(2,2))
> ylim <- c(min(Nile),max(Nile))
> plot(Nile,main="Raw time series")
> plot(ma(Nile,3),main="Simple Moving Averages (k=3)",ylim=ylim)
> plot(ma(Nile,7),main="Simple Moving Averages (k=7)",ylim=ylim)
> plot(ma(Nile,15),main="Simple Moving Averages (k=15)",ylim=ylim)
> par(opar)

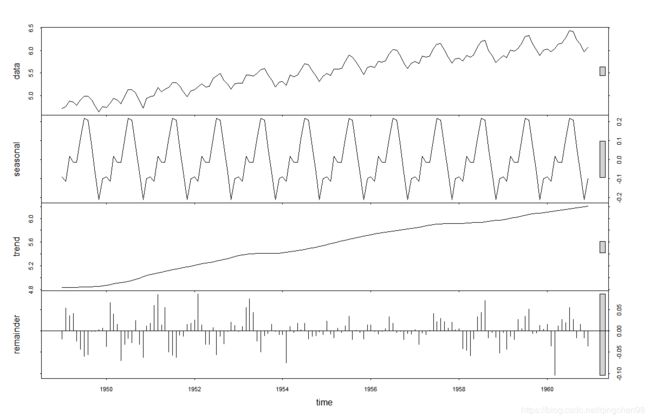
存在季节性因素的时序数据(如月度数据,季度数据)可以分解为趋势因子、季节因子和随机因子。其中,趋势因子(trend compoent)能捕捉到长期变化,季节因子(seasonal compoent)能捕捉到一年内的周期变化,而随机(误差)因子(irregular/error component)则能捕捉到那些不能被趋势或季节效应解释的变化。
plot(AirPassengers)
> lAirpassengers <- log(AirPassengers)
> plot(lAirpassengers,ylab="log(AirPassengers)")
> fit <- stl(lAirpassengers,s.window = "period")
> plot(fit)
#季节分解可视化(seasonal visualization)
> par(mfrow=c(2,1))
> library(forecast)
> monthplot(AirPassengers,xlab="",ylab = "")
> seasonplot(AirPassengers,year.labels = "TRUE",main = "")
> par(opar)
3. 预测
预测是时间序列数据分析最重要的一个环节,指数模型是用来预测时序未来值的最常用模型,这类模型比较简单,实践证明它们的短期预测能力较好。不同指数模型建模时选用的因子可能不同,单指数模型拟合的是只有常数水平项和时间点i处的时间序列,这是认为时间序列不存在趋势项和季节效应,双指数模型拟合的是有水平项和趋势项的时序,三指数模型预测的是由水平项、趋势项和季节效应的时序。
- 单指数平滑
> #单指数平滑(simple/single exponential model)
> data("nhtemp")
> plot(nhtemp,main="New Haven Annual Mean Temperature",xlab="year",
+ ylab="Temperature(℉)")
> library(forecast)
> fit <- ets(nhtemp,model = "ANN") #其中A表示可加误差,NN表示时序中不存在趋势项和季节项
> fit
ETS(A,N,N)
Call:
ets(y = nhtemp, model = "ANN")
Smoothing parameters:
alpha = 0.1819
Initial states:
l = 50.2762
sigma: 1.1455
AIC AICc BIC
265.9298 266.3584 272.2129
> forecast(fit,1) #一步向前预测(One step ahead)
Point Forecast Lo 80 Hi 80 Lo 95 Hi 95
1972 51.87031 50.40226 53.33835 49.62512 54.11549
> accuracy(fit) #预测准确度(predictive accuracy)
ME RMSE MAE MPE MAPE MASE ACF1
Training set 0.1460657 1.126268 0.8951225 0.2419373 1.7489 0.7512408 -0.006441923
- Holt指数平滑和Holt-Winters指数平滑
> #Holt指数平滑和Holt-Winters指数平滑
> library(forecast)
> fit <- ets(log(AirPassengers),model = "AAA") #AAA分别表示可加误差、趋势项和季节项
> fit
ETS(A,A,A)
Call:
ets(y = log(AirPassengers), model = "AAA")
Smoothing parameters:
alpha = 0.6975
beta = 0.0031
gamma = 1e-04
Initial states:
l = 4.7925
b = 0.0111
s = -0.1045 -0.2206 -0.0787 0.0562 0.2049 0.2149
0.1146 -0.0081 -0.0059 0.0225 -0.1113 -0.0841
sigma: 0.0383
AIC AICc BIC
-207.1694 -202.3123 -156.6826
> accuracy(fit)
ME RMSE MAE MPE MAPE MASE ACF1
Training set -0.001830684 0.03606976 0.02770885 -0.03435608 0.5079142 0.2289192 0.05590461
> pred <- forecast(fit,5)
> pred
Point Forecast Lo 80 Hi 80 Lo 95 Hi 95
Jan 1961 6.109335 6.060306 6.158365 6.034351 6.184319
Feb 1961 6.092542 6.032679 6.152405 6.000989 6.184094
Mar 1961 6.236626 6.167535 6.305718 6.130960 6.342292
Apr 1961 6.218531 6.141239 6.295823 6.100323 6.336738
May 1961 6.226734 6.141971 6.311498 6.097100 6.356369
> plot(pred,main = "Forecast for Air Travel",xlab = "Time",
+ ylab = "Log(Airpassengers)")
> pred$mean <- exp(pred$mean)
> pred$lower <- exp(pred$lower)
> pred$upper <- exp(pred$upper)
> p <- cbind(pred$mean,pred$lower,pred$upper)
> p
pred$mean pred$lower.80% pred$lower.95% pred$upper.80% pred$upper.95%
Jan 1961 450.0395 428.5065 417.5279 472.6544 485.0826
Feb 1961 442.5448 416.8301 403.8280 469.8459 484.9735
Mar 1961 511.1312 477.0088 459.8775 547.6945 568.0971
Apr 1961 501.9652 464.6289 446.0019 542.3017 564.9506
May 1961 506.1001 464.9691 444.5667 550.8694 576.1504
- ets()函数自动预测
ets()函数还可以用来拟合有可乘项的指数模型,加入抑制因子(damping component),以及进行自动预测。以下代码展示了没有指定模型,因此软件会自动搜索一系列模型,并在其中找到最小化拟合标准的模型。
#ets()函数自动预测
> library(forecast)
> fit <- ets(JohnsonJohnson)
> fit
ETS(M,A,A)
Call:
ets(y = JohnsonJohnson)
Smoothing parameters:
alpha = 0.2776
beta = 0.0636
gamma = 0.5867
Initial states:
l = 0.6276
b = 0.0165
s = -0.2293 0.1913 -0.0074 0.0454
sigma: 0.0921
AIC AICc BIC
163.6392 166.0716 185.5165
> forecast(fit)
Point Forecast Lo 80 Hi 80 Lo 95 Hi 95
1981 Q1 17.53691 15.46779 19.60602 14.372463 20.70135
1981 Q2 16.20101 14.16229 18.23972 13.083060 19.31895
1981 Q3 17.50409 15.17989 19.82829 13.949531 21.05865
1981 Q4 13.18744 11.07225 15.30263 9.952541 16.42234
1982 Q1 19.07616 15.57336 22.57896 13.719095 24.43322
1982 Q2 17.74026 14.20782 21.27270 12.337865 23.14265
1982 Q3 19.04334 15.10196 22.98473 13.015511 25.07118
1982 Q4 14.72670 10.99126 18.46213 9.013844 20.43955
> plot(forecast(fit),main = "Johnson & Johnson Forecast",
+ ylab = "Quarterly Earnings (Dollars)",xlab = "Time",flty = 2)

所选中的模型同时有可乘项趋势项、季节项和随机误差项,上图给出了其折线图以及下八个季度(默认)的预测,flty参数指定了图中预测值折线的类型(虚线)。
小结
尽管这些方法对于理解、预测很多现象都十分关键,但这些方法都用到了向外推断的思想,即它们假设未来的条件和现在的条件是相似的。比如2007年的金融预测就认为2008年以后的经济状况会与2007年一样稳定,但事实并不是这样。很多事情都可能改变序列中的趋势和模式,你想预测的时间跨度越大,不确定性就越大。
致谢:
感谢《R语言实战(第2版)》一书,对R语言学习有很大的帮助,以上代码来自该书。
RobertI.Kabacoff, 王小宁,等. R语言实战(第2版)[J]. 2016.