HanLP《自然语言处理入门》笔记--3.二元语法与中文分词
文章目录
- 3. 二元语法与中文分词
- 3.1 语言模型
- 3.2 中文分词语料库
- 3.3 训练与预测
- 3.4 HanLP分词与用户词典的集成
- 3.5 二元语法与词典分词比较
- 3.6 GitHub项目
笔记转载于GitHub项目:https://github.com/NLP-LOVE/Introduction-NLP
3. 二元语法与中文分词
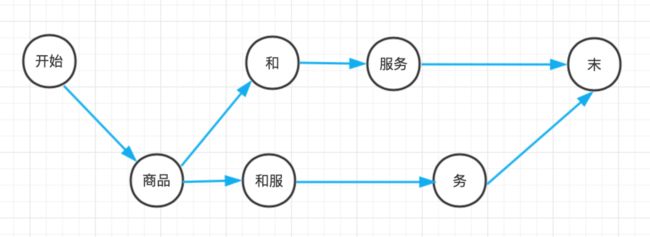
上一章中我们实现了块儿不准的词典分词,词典分词无法消歧。给定两种分词结果“商品 和服 务”以及“商品 和 服务”,词典分词不知道哪种更加合理。
我们人类确知道第二种更加合理,只因为我们从小到大接触的都是第二种分词,出现的次数多,所以我们判定第二种是正确地选择。这就是利用了统计自然语言处理。统计自然语言处理的核心话题之一,就是如何利用统计手法对语言建模,这一章讲的就是二元语法的统计语言模型。
3.1 语言模型
-
什么是语言模型
模型指的是对事物的数学抽象,那么语言模型指的就是对语言现象的数学抽象。准确的讲,给定一个句子 w,语言模型就是计算句子的出现概率 p(w) 的模型,而统计的对象就是人工标注而成的语料库。
假设构建如下的小型语料库:
商品 和 服务 商品 和服 物美价廉 服务 和 货币每个句子出现的概率都是 1/3,这就是语言模型。然而 p(w) 的计算非常难:句子数量无穷无尽,无法枚举。即便是大型语料库,也只能“枚举”有限的数百万个句子。实际遇到的句子大部分都在语料库之外,意味着它们的概率都被当作0,这种现象被称为数据稀疏。
句子几乎不重复,单词却一直在重复使用,于是我们把句子表示为单词列表 w = w 1 w 2 . . . w k w=w_1w_2...w_k w=w1w2...wk ,每个 w t , t ∈ [ 1 , k ] w_t,t\in[1,k] wt,t∈[1,k] 都是一个单词,然后定义语言模型:
p ( w ) = p ( w 1 w 2 ⋯ w k ) = p ( w 1 ∣ w 0 ) × p ( w 2 ∣ w 0 w 1 ) × ⋯ × p ( w k + 1 ∣ w 0 w 1 w 2 … w k ) = ∏ t = 1 k + 1 p ( w t ∣ w 0 w 1 ⋯ w t − 1 ) \begin{aligned} p(\boldsymbol{w}) &=p\left(w_{1} w_{2} \cdots w_{k}\right) \\ &=p\left(w_{1} | w_{0}\right) \times p\left(w_{2} | w_{0} w_{1}\right) \times \cdots \times p\left(w_{k+1} | w_{0} w_{1} w_{2} \dots w_{k}\right) \\ &=\prod_{t=1}^{k+1} p\left(w_{t} | w_{0} w_{1} \cdots w_{t-1}\right) \end{aligned} p(w)=p(w1w2⋯wk)=p(w1∣w0)×p(w2∣w0w1)×⋯×p(wk+1∣w0w1w2…wk)=t=1∏k+1p(wt∣w0w1⋯wt−1)
其中, w 0 = B O S w_0=BOS w0=BOS (Begin Of Sentence,有时用), w k + 1 = E O S ( E n d O f S e n t e n c e , 有 时 也 用 < / s > ) w_{k+1}=EOS (End Of Sentence,有时也用) wk+1=EOS(EndOfSentence,有时也用</s>),是用来标记句子收尾的两个特殊“单词”,在NLP领域的文献和代码中经常出现。然而随着句子长度的增大,语言模型会遇到如下两个问题。
- 数据稀疏,指的是长度越大的句子越难出现,可能统计不到频次,导致 p ( w k ∣ w 1 w 2 . . . w k − 1 ) = 0 p(w_k|w_1w_2...w_{k-1})=0 p(wk∣w1w2...wk−1)=0,比如 p(商品 和 货币)=0。
- 计算代价大,k 越大,需要存储的 p 就越多,即便用上字典树索引,依然代价不菲。
-
马尔可夫链与二元语法
为了解决以上两个问题,需要使用马尔可夫假设来简化语言模型,给定时间线上有一串事件顺序发生,假设每个事件的发生概率只取决于前一个事件,那么这串事件构成的因果链被称作马尔可夫链。
在语言模型中,第 t 个事件指的是 w t w_t wt 作为第 t 个单词出现。也就是说,每个单词出现的概率只取决于前一个单词:
p ( w t ∣ w 0 w 1 . . . w t − 1 ) = p ( w t ∣ w t − 1 ) p(w_t|w_0w_1...w_{t-1})=p(w_t|w_{t-1}) p(wt∣w0w1...wt−1)=p(wt∣wt−1)
基于此假设,式子一下子变短了不少,此时的语言模型称为二元语法模型:
p ( w ) = p ( w 1 w 2 ⋯ w k ) = p ( w 1 ∣ w 0 ) × p ( w 2 ∣ w 1 ) × ⋯ × p ( w k + 1 ∣ w k ) = ∏ t = 1 k + 1 p ( w t ∣ w t − 1 ) \begin{aligned} p(\boldsymbol{w}) &=p\left(w_{1} w_{2} \cdots w_{k}\right) \\ &=p\left(w_{1} | w_{0}\right) \times p\left(w_{2} | w_{1}\right) \times \cdots \times p\left(w_{k+1} | w_{k}\right) \\ &=\prod_{t=1}^{k+1} p\left(w_{t} | w_{t-1}\right) \end{aligned} p(w)=p(w1w2⋯wk)=p(w1∣w0)×p(w2∣w1)×⋯×p(wk+1∣wk)=t=1∏k+1p(wt∣wt−1)
由于语料库中二元连续的重复程度要高于整个句子的重要程度,所以缓解了数据稀疏的问题,另外二元连续的总数量远远小于句子的数量,存储和查询也得到了解决。 -
n元语法
利用类似的思路,可以得到n元语法的定义:每个单词的概率仅取决于该单词之前的 n 个单词:
p ( w ) = ∏ t = 1 k + n − 1 p ( w t ∣ w t − n + 1 … w t − 1 ) p(w)=\prod_{t=1}^{k+n-1} p\left(w_{t} | w_{t-n+1} \dots w_{t-1}\right) p(w)=t=1∏k+n−1p(wt∣wt−n+1…wt−1)
特别地,当 n=1 时的 n 元语法称为一元语法 ( unigram);当 n=3 时的 n 元语法称为三元语法(tigam); n≥4时数据稀疏和计算代价又变得显著起来,实际工程中几乎不使用。 -
数据稀疏与平滑策略
对于 n 元语法模型,n 越大,数据稀疏问题越严峻。比如上述语料库中“商品 货币”的频次就为0。一个自然而然的解决方案就是利用低阶 n 元语法平滑高阶 n 元语法,所谓平滑,就是字面上的意思:使 n 元语法频次的折线平滑为曲线。最简单的一种是线性插值法:
p ( w t ∣ w t − 1 ) = λ p M L ( w t ∣ w t − 1 ) + ( 1 − λ ) p ( w t ) p\left(w_{t} | w_{t-1}\right)=\lambda p_{\mathrm{ML}}\left(w_{t} | w_{t-1}\right)+(1-\lambda) p\left(w_{t}\right) p(wt∣wt−1)=λpML(wt∣wt−1)+(1−λ)p(wt)
其中, λ ∈ ( 0 , 1 ) \lambda\in(0,1) λ∈(0,1) 为常数平滑因子。通俗理解,线性插值就是劫富济贫的税赋制度,其中的 λ 就是个人所得税的税率。 p M L ( w t ∣ w t − 1 ) p_{ML}(w_t|w_{t-1}) pML(wt∣wt−1) 是税前所得, p ( w t ) p(w_t) p(wt) 是社会福利。 通过缴税,高收人(高概率)二元语法的一部分收人 (概率)被移动到社会福利中。而零收入(语料库统计不到频次)的一元语法能够从社会福利中取得点低保金, 不至于饿死。低保金的额度与二元语法挣钱潜力成正比:二元语法中第二个词词频越高,它未来被统计到的概率也应该越高,因此它应该多拿一点。类似地,一元语法也可以通过线性插值来平滑:
p ( w t ) = λ p M L ( w t ) + ( 1 − λ ) 1 N p\left(w_{t}\right)=\lambda p_{\mathrm{ML}}\left(w_{t}\right)+(1-\lambda) \frac{1}{N} p(wt)=λpML(wt)+(1−λ)N1
其中,N 是语料库总词频。
3.2 中文分词语料库
语言模型只是一个函数的骨架,函数的参数需要在语料库上统计才能得到。为了满足实际工程需要,一个质量高、分量足的语料库必不可少。以下是常用的语料库:
- 《人民日报》语料库 PKU
- 微软亚洲研究院语料库 MSR
- 香港城市大学 CITYU(繁体)
- 台湾中央研究院 AS(繁体)
| 语料库 | 字符数 | 词语种数 | 总词频 | 平均词长 |
|---|---|---|---|---|
| PKU | 183万 | 6万 | 111万 | 1.6 |
| MSR | 405万 | 9万 | 237万 | 1.7 |
| AS | 837万 | 14万 | 545万 | 1.5 |
| CITYU | 240万 | 7万 | 146万 | 1.7 |
一般采用MSR作为分词语料的首选,有以下原因:
- 标注一致性上MSR要优于PKU。
- 切分颗粒度上MSR要优于PKU,MSR的机构名称不予切分,而PKU拆开。
- MSR中姓名作为一个整体,更符合习惯。
- MSR量级是PKU的两倍。
3.3 训练与预测
训练指的是统计二元语法频次以及一元语法频次,有了频次,通过极大似然估计以及平滑策略,我们就可以估计任意句子的概率分布,即得到了语言模型。这里以二元语法为例:
这里我们选用上面自己构造的小型语料库:data/dictionnary/my_cws_corpus.txt
代码请见:code/ch03/ngram_segment.py
步骤如下:
-
加载语料库文件并进行词频统计。
-
对词频文件生成词网
词网指的是句子中所有一元语法构成的网状结构,是HanLP工程上的概念。比如“商品和服务”这个句子,我们将句子中所有单词找出来,起始位置(offset)相同的单词写作一行:
0:[ ] 1:[商品] 2:[] 3:[和,和服] 4:[服务] 5:[务] 6:[ ]其中收尾(行0和行6)分别对应起始和末尾。词网必须保证从起点出发的所有路径都会连通到钟点房。
词网有一个极佳的性质:那就是第 i 行的词语 w 与第 i+len(w) 行的所有词语相连都能构成二元语法。
-
词图上的维特比算法
上述词图每条边以二元语法的概率作为距离,那么中文分词任务转换为有向无环图上的最长路径问题。再通过将浮点数乘法转化为负对数之间的加法,相应的最长路径转化为负对数的最短路径。使用维特比算法求解。
这里仅作一下简述,详细过程参考书本第三章。
该模型代码输入是句子“货币和服务”,得到结果如下:
[' ', '货币', '和', '服务', ' ']
结果正确,可见我们的二元语法模型具备一定的泛化能力。
3.4 HanLP分词与用户词典的集成
词典往往廉价易得,资源丰富,利用统计模型的消歧能力,辅以用户词典处理新词,是提高分词器准确率的有效方式。HanLP支持 2 档用户词典优先级:
- 低优先级:分词器首先在不考虑用户词典的情况下由统计模型预测分词结果,最后将该结果按照用户词典合并。默认低优先级。
- 高优先级:分词器优先考虑用户词典,但具体实现由分词器子类自行决定。
HanLP分词器简洁版:
from pyhanlp import *
ViterbiSegment = SafeJClass('com.hankcs.hanlp.seg.Viterbi.ViterbiSegment')
segment = ViterbiSegment()
sentence = "社会摇摆简称社会摇"
segment.enableCustomDictionary(False)
print("不挂载词典:", segment.seg(sentence))
CustomDictionary.insert("社会摇", "nz 100")
segment.enableCustomDictionary(True)
print("低优先级词典:", segment.seg(sentence))
segment.enableCustomDictionaryForcing(True)
print("高优先级词典:", segment.seg(sentence))
输出:
不挂载词典: [社会/n, 摇摆/v, 简称/v, 社会/n, 摇/v]
低优先级词典: [社会/n, 摇摆/v, 简称/v, 社会摇/nz]
高优先级词典: [社会摇/nz, 摆/v, 简称/v, 社会摇/nz]
可见,用户词典的高优先级未必是件好事,HanLP中的用户词典默认低优先级,做项目时请读者在理解上述说明的情况下根据实际需求自行开启高优先级。
3.5 二元语法与词典分词比较
按照NLP任务的一般流程,我们已经完成了语料标注和模型训练,现在来比较一下二元语法和词典分词的评测:
| 算法 | P | R | F1 | R(oov) | R(IV) |
|---|---|---|---|---|---|
| 最长匹配 | 89.41 | 94.64 | 91.95 | 2.58 | 97.14 |
| 二元语法 | 92.38 | 96.70 | 94.49 | 2.58 | 99.26 |
相较于词典分词,二元语法在精确度、召回率及IV召回率上全面胜出,最终F1值提高了 2.5%,成绩的提高主要受惠于消歧能力的提高。然而 OOV 召回依然是 n 元语法模型的硬伤,我们需要更强大的语言模型。
3.6 GitHub项目
HanLP何晗–《自然语言处理入门》笔记:
https://github.com/NLP-LOVE/Introduction-NLP
项目持续更新中…
目录
| 章节 |
|---|
| 第 1 章:新手上路 |
| 第 2 章:词典分词 |
| 第 3 章:二元语法与中文分词 |
| 第 4 章:隐马尔可夫模型与序列标注 |
| 第 5 章:感知机分类与序列标注 |
| 第 6 章:条件随机场与序列标注 |
| 第 7 章:词性标注 |
| 第 8 章:命名实体识别 |
| 第 9 章:信息抽取 |
| 第 10 章:文本聚类 |
| 第 11 章:文本分类 |
| 第 12 章:依存句法分析 |
| 第 13 章:深度学习与自然语言处理 |