流问题Flow Problem(网络最大流)- HDU 3549
网络最大流问题属于算法 里面较难的问题,因为牵涉的概念比较多,这一篇可能需要你花比较多的时间去理解,除了看这个,最好能多参考别的书籍或者文章进行比较学习,不然可能容易产生理解的偏差。
另外本公众号并不打算讲解过于复杂的问题,网络流问题已经严重超过了最初设想的五分钟限制,不过由于是第一篇网络流的题目,可以作为后面相关问题的基础,姑且多写点。如果你觉得一次难以看懂,可以在时间多的时候看看。
网络流,顾名思义,可以认为是网络通信的流量,也可以想象成水管里水的流动情况,存在节点和边,每条边有容量且不一样(管道大小不一)。
最大网络流就是要寻找从节点s到节点t的能够取得的最大流量。
1、容量网络:定义图G是一个有向图(网络),对于每一条边,有一个权重c,这个权重c表示这条边的容量capacity。
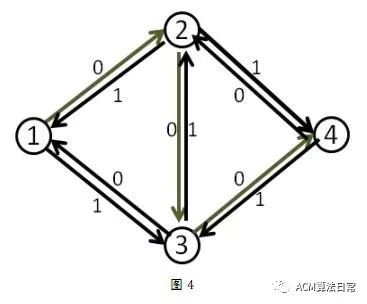
2、对于上图,要找出从s到t的最大网络流,首先我们看几个定义。
3、流f:流f是指从s到t一条路径上的流量,可以看成是一条水流。
4、残存网络:对于G,减去一条流f后的网络,网络G在这条路径上的边容量需要减去流f的值。也就是说这个路径被流f占用了。
5、增广路径:给定流网络G和流f,增广路径是指残存网络中一条从源结点s 到汇点t的简单路径(路径中不存在重复的顶点或边 )。 简单的说就是一条从s到t的路径。对于上图中s-v1-v3-t就是一条增广路径。
6、反向流量:反向流量初始为0,每次减去一条增广路径后,我们要在边信息上加上反向流量值,反向流量的作用比较微妙,如图:
对于增广路径1-2-3-4,从G中减去之后,1-2、2-3、3-4都为0,这时候就找不到增广路径了,加上反向流量后:
这时候就能找到1-3-2-4这条增广路径了。
7、层次:在剩余图中, 我们把从源点到点 u 的最短路径长度称作点 u 的层次, 记为level(u)。 源点s的层次为 0。直观地讲, 层次图是建立在剩余图基础之上的一张“最短路图”。 从源点开始,在层次图中沿着边不管怎么走,经过的路径一定是终点在剩余图中的最短路。
算法思路整理:
1、每次迭代采用广度优先计算当前G的层次属性;
2、采用深度优先的方式来搜索所有的路径并计算出流f的值;
3、更新G(减去增广路径,计算反向流量);
4、如果找不到增广路径,则当前流的和就是最大流。
Problem Description
Network flow is a well-known difficult problem for ACMers. Given a graph, your task is to find out the maximum flow for the weighted directed graph.
对于Acmer来说,网络流是出名的难。给定一个图,找出最大的流。
Input
The first line of input contains an integer T, denoting the number of test cases.
For each test case, the first line contains two integers N and M, denoting the number of vertexes and edges in the graph. (2 <= N <= 15, 0 <= M <= 1000)
Next M lines, each line contains three integers X, Y and C, there is an edge from X to Y and the capacity of it is C. (1 <= X, Y <= N, 1 <= C <= 1000)
第一行输入包含一个整数T,表示有T个测试用例。
对于每个测试用例,第一行是整数N和M,分别表示定点数和边的个数。下面有M行,每行是三个整数X/Y/C,其中X/Y表示从X到Y,C是容量(权重)。
Output
For each test cases, you should output the maximum flow from source 1 to sink N.
对于每个测试用例,输出最大从节点1到N的最大流。
Sample Input
2
3 2
1 2 1
2 3 1
3 3
1 2 1
2 3 1
1 3 1
Sample Output
Case 1: 1
Case 2: 2
解题思路:套用最大流算法思路。
最大流的理解比较花时间,每个概念都可能产生误解,建议一边看代码一边理解最大流的算法思想。
源码:G++ 156ms
#include
#include
#include
#include
#include
#include
#include
using namespace std;
#define INFINITE 10000000
const int maxn = 1000;
//边信息
typedef struct edge_s {
int to; //下一个节点
int cap; //容量capacity
int reverse; //反向节点
}edge_t;
//所有的边信息
vector G[maxn];
//层次信息
int level[maxn];
//迭代信息
int iter[maxn];
void add_edge(int from, int to, int cap) {
//正向图
G[from].push_back({to, cap, (int)G[to].size() });
//反向图
G[to].push_back({from, 0, (int)G[from].size() - 1});
}
//构造分层图O(E),最多进行V-1次
//s是开始,level[u]是指从起点s到点u的最短路径长度
//广度优先搜索使用队列完成搜索树的遍历,层层递进计算长度
void bfs(int start) {
//每次迭代,重置level中所有的值为-1
memset(level, -1, sizeof(level));
//队列
queue bfs_queue;
//开始节点的level设置为0
level[start] = 0;
//放入开始节点
bfs_queue.push(start);
while (!bfs_queue.empty()) {
//取出头结点
int from = bfs_queue.front();
bfs_queue.pop();
int size = G[from].size();
for (int i = 0; i < G[from].size(); i++) {
//对于from表,取出
edge_t &e = G[from][i];
//e表示边信息
if (e.cap > 0 && level[e.to] < 0) {
//每发现一个下级节点,层次+1
level[e.to] = level[from] + 1;
//放入队列继续
bfs_queue.push(e.to);
}
}
}
}
//深度优先搜索,寻找最短增广路径
int dfs(int x, int t, int f) {
//如果起点与终点相同,搜索到终点了,返回这条路径上的最小值
if (x == t)
return f;
//注意这里的i是引用,能够改变iter[x]的值
for (int &i = iter[x]; i < G[x].size(); i++) {
edge_t &e = G[x][i];
//只会往深处寻找level
if (e.cap > 0 && level[x] < level[e.to]) {
//接着从下一个节点向t搜索
//取得较小值,通过递归搜索,可以遍历所有的路径,遍历的过程中更新所有边的最小值
int d = dfs(e.to, t, min(f, e.cap));
if (d > 0) {
//cap减1
e.cap -= d;
//反向边加上减去的流量
G[e.to][e.reverse].cap += d;
return d;
}
}
}
return 0;
}
//s是开始,t是结束
int max_flow(int s, int t) {
int flow = 0;
for (;;) {
//广度优先,计算层次信息
bfs(s);
//如果level小于0,说明找不到路径
if (level[t] < 0) return flow;
//设置iter为0
memset(iter, 0, sizeof(iter));
int f;
//深度优先,f大于0表示存在路径
while ((f = dfs(s, t, INFINITE)) > 0)
flow += f;
}
return flow;
}
int main()
{
int n, m, Case = 0;
int T;
scanf("%d", &T);
while (T--) {
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i++) G[i].clear();
//依次输入边信息
for (int i = 1; i <= m; i++) {
int x, y, cap;
scanf("%d%d%d", &x, &y, &cap);
add_edge(x, y, cap);
}
//从节点1到n
int ans = max_flow(1, n);
printf("Case %d: %d\n", ++Case, ans);
}
return 0;
} 个人公众号:ACM算法日常
专注于基础算法的研究工作,深入解析ACM算法题,五分钟阅读,轻松理解每一行源代码。内容涉及算法、C/C++、机器学习等。
![]()