一文了解目标检测边界框概率分布

众所周知，CNN的有监督学习通常是建立在给定训练数据集之上的，数据集的标签(也称为GT)，决定了人类期望模型学习的样子。它通过损失函数、优化器等与CNN模型相连。因而机器所表现的出的一切有关识别、定位的能力，均是合理优化的结果。同样地，如何能够玩转目标检测？其实只需能够玩转最优化即可。

在最近两年内，出现了一些有关目标检测bounding box概率分布建模的文章，如Softer-NMS (CVPR 2019)，Gaussian YOLOv3 (ICCV 2019)，An Alternative Probabilistic Interpretation of the Huber Loss (Arxiv 2019.11)，Generalized Focal Loss (Arxiv 2020.06)，本文将主要通过以上四篇文章进行阐述。

目标检测的概率分布建模，首次出现于Softer-NMS (to my best knowledge)，其文章主旨基于一个最基本的观察：bounding box标签存在模棱两可的区域。所谓模棱两可的区域正如上图的火车，它的左、上、下边界都是较为确定的，而右边界却是模棱两可的，因为它包含了一些非目标区域。可以说，对于右边界而言，往左偏移一点与往右偏移一点都是可接受的，这就是它的模糊性。

接下来再考察我们的bounding box regression模块，模型的监督信息只有四个值x，y，w，h (中心点坐标与宽高)，或者x1，y1，x2，y2(左上角点与右下角点坐标)，亦或者t，b，l，r (采样点到上下左右四条边的距离)。而所选用的损失函数，通常为Ln范数损失，如L1，L2，Smooth L1损失，或者基于IoU的损失。

关于目标检测box回归损失函数，可以参考目标检测回归损失函数简介：SmoothL1/IoU/GIoU/DIoU/CIoU Loss

然而以上这些损失函数均以模型预测值和GT值比较作为反向传播的依据，这缺乏了对数据标签不确定性的估计。如果我们能够得到一个box的定位不确定程度，则我们可以加以利用以提升模型的精度。

常用的一些手段包括：

惩罚分类得分 (Mask Scoring R-CNN CVPR 2019, Gaussian YOLOv3 ICCV 2019, FCOS ICCV 2019, PolarMask CVPR 2020)、加权平均后处理 (Softer-NMS CVPR 2019)，引导NMS (IoU-Net ECCV 2018)。

概率建模

传统的box预测只有四个输出值，对于每一个输出值，等同于优化一个狄拉克分布

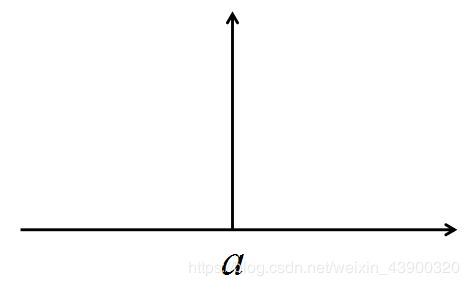
也即一个在给定区间上积分为1的概率分布，其只在$x=a$处有监督信号，而在其余地方没有监督。

为了引入box的不确定性估计，Softer-NMS与Gaussian YOLOv3均采取了高斯建模的方法，将模型的预测值由4个变为8个，分别代表四条边的均值与方差，其中方差代表了不确定性的程度。

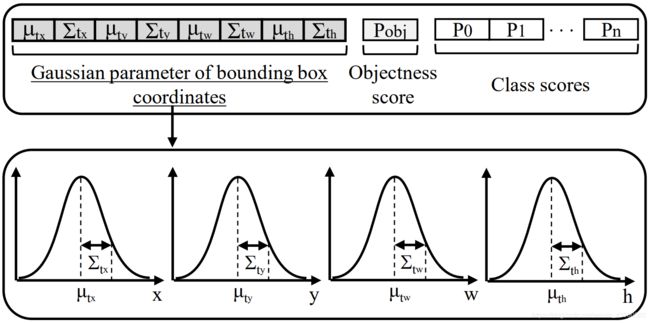
我们知道高斯分布当方差越大时，分布越为平坦，表明了模型对均值范围内的预测不确定；方差越小时，分布越尖锐，表明模型对均值位置处的预测很自信。

从数学上来看，我们只需要一些衡量两个概率分布相似程度的损失函数，如KL散度，就能够做到用高斯分布去拟合狄拉克分布。

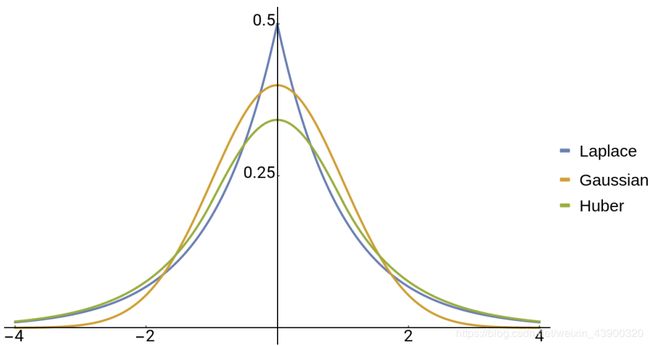
在An Alternative Probabilistic Interpretation of the Huber Loss中，研究者首先解释了Ln范数损失与概率分布之间的联系。总结来说：

1. 当选用L1损失时，等价于优化一个不确定度满足拉普拉斯分布的似然估计。

2. 当选用L2损失时，等价于优化一个不确定度满足高斯分布的似然估计。

3. 当选用Huber损失时(也即Smooth L1损失)，等价于优化一个不确定度满足特定值的拉普拉斯分布，而这个不确定度与Huber损失中所选用的L1损失和L2损失的转折点 $\alpha$ 有直接联系。

因此，与Softer-NMS和Gaussian YOLOv3不同的是，该文将视线转移到了Huber损失中转折点 $\alpha$ 的选用是否合适上。经过一系列理论推导，论文得出的结论是，目前的Smooth L1损失中所选用的转折点 $\alpha$ 是有问题的。

该文将转折点 $\alpha$ 与不确定度关联起来，得出了如下结果：

1. GT作为人类预测的结果，其不确定度应该比模型预测要小。

2. RPN是粗定位阶段，其不确定度理应比Fast R-CNN精细定位阶段大。

而由目前的Smooth L1的转折点 $\alpha$ 推导出的不确定性，都违反了以上两个直觉。因此该文后续的改进主要是对 $\alpha$ 进行调整。

缺点：以上这些概率建模方式，依然没有脱离对box的四个变量独立预测，无法享用目前最新的一些IoU-based损失的好处。

在Generalized Focal Loss一文中，研究者尝试建模一个一般的概率分布。

既然狄拉克分布太严格了，缺乏对不确定度的估计，而高斯分布又是一种简化版本，且实际的数据所满足的概率分布应该是任意的，因此一般概率分布的建模也就应运而生。

一般分布的建模，有个直接问题是无法使用较少参数将一个连续且任意的概率分布描述出来，因此必须采取离散法。大致方法是将给定区间分成n个间隔均匀的小区间，网络输出n+1个预测值，分别代表概率。

这些概率都经过了Softmax输出，且满足概率和为1。

$\sum _{i}P(x_i)=1$

按照加权和，即可得到某条边的预测值$x=\sum _{i}P(x_i)x_i$

论文选用了FCOS作为基础框架，由于FCOS在边界框回归上是采取预测采样点到上、下、左、右四条边的距离，这使得回归目标的长度较为统一，可以很好地在一个固定区间上表示出来。

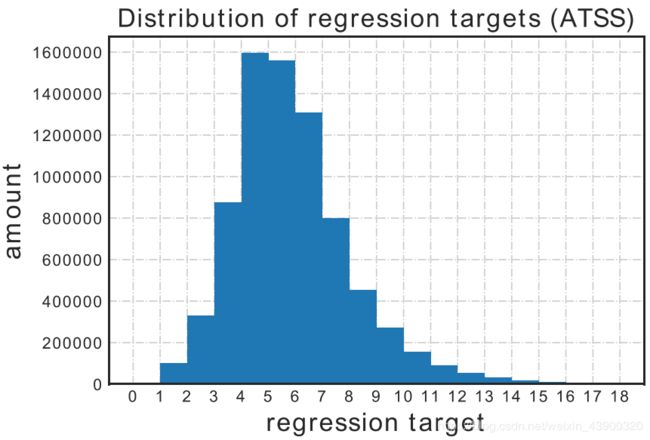
好处：

1. 一般分布更为灵活，可以更好地应对现实世界的复杂数据。
2. 可以享受IoU-based损失，而高斯分布无法直接享用。
3. 一般分布可以预测出双峰型的分布，这或许隐含了一些对数据集模棱两可位置的信息，有可能可以用于进一步数据标签校正。

从效果来看一般分布建模取得了最好的结果。

这里表格的最后一行代表使用了DFL (Distribution Focal Loss)，用于额外加强GT所属的小区间端点的学习，加速模型收敛。

参考文献

• Bounding Box Regression with Uncertainty for Accurate Object Detection. CVPR 2019
• Gaussian YOLOv3: An Accurate and Fast Object Detector Using Localization Uncertainty for Autonomous Driving. ICCV 2019
• An Alternative Probabilistic Interpretation of the Huber Loss. Arxiv 2019.11
• Generalized Focal Loss: Learning Qualified and Distributed Bounding Boxes for Dense Object Detection. Arxiv 2020.06
• Acquisition of Localization Confidence for Accurate Object Detection. ECCV 2018
• Mask Scoring R-CNN. CVPR 2019
• FCOS: A simple and strong anchor-free object detector. ICCV 2019
• PolarMask: Single Shot Instance Segmentation with Polar Representation. CVPR 2020