《剑指offer》二叉树的最近公共祖先--递归解决

0x01.问题

给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个结点 p、q，最近公共祖先表示为一个结点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

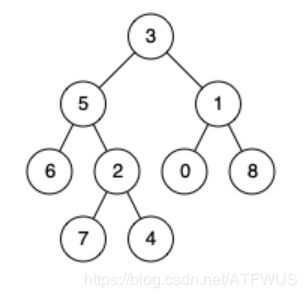
例如，给定如下二叉树: root = [3,5,1,6,2,0,8,null,null,7,4]

示例 1:

输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出: 3
解释: 节点 5 和节点 1 的最近公共祖先是节点 3。

示例 2:

输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
输出: 5
解释: 节点 5 和节点 4 的最近公共祖先是节点 5。因为根据定义最近公共祖先节点可以为节点本身。

说明:

• 所有节点的值都是唯一的。
• p、q 为不同节点且均存在于给定的二叉树中。

0x02.分析思路

读懂题目，明确公共祖先的概念，公共祖先root应该有以下几种可能。

• p，q位于root的两侧（也就是说p，q是root的子树，且在不同侧）
• root=p，q位于root的左子树或者右子树。
• root=q，p位于root的左子树或者右子树。

接下来就是如何去寻找最近的公共祖先了，最近，也就是深度最大的公共祖先，这就暗示着我们，如果从叶子节点开始寻找，那么，找到的第一个，就是最近的，这种寻找的方式，其实也就是后序遍历的方法。

假设，我们通过后序遍历的方式找到了最近的，如何确保在后面的递归步骤中不会更新呢？

• 很简单，在找到第一个公共祖先后，后面找到的公共祖先都不可能满足这个条件，因为这个最近的公共祖先也成为别人的子树时，对于其它的公共祖先，就不可能满足上述条件了，即p，q已经在一侧了。

具体算法思路：

• 核心判断语句：( lcontain && rcontain )||((root==p || root==q)&&(lcontain||rcontain)).

  • lcontain代表，左子树存在p或q。
  • rcontain代表，右子树存在p或q。

• 寻找方式采用后序的方式，从叶子节点到根节点。

具体代码如下：

0x03.解决代码–递归

class Solution {
    private TreeNode ans;
    private Boolean dfs(TreeNode root,TreeNode p,TreeNode q){
        if(root==null){
            return false;
        }
        Boolean lcontain=dfs(root.left,p,q);
        Boolean rcontain=dfs(root.right,p,q);
        if((lcontain&&rcontain)||(root.val==p.val||root.val==q.val)&&(lcontain||rcontain)){
            ans=root;
        }
        return lcontain||rcontain||(root.val==p.val||root.val==q.val);
    }
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        dfs(root,p,q);
        return ans;
    }
}

ATFWUS --Writing By 2020–05-11