感知算法论文（八）：Generalized Intersection over Union：A Metric and A Loss for Bounding Box Regression（2019）

摘要

Intersection over Union（IoU）是目标检测领域应用最多的度量方式。

优化b-box的参数的回归过程所使用的损失函数和最大化度量值之间存在一定的鸿沟

二维轴心对齐的b-box情况，IoU可以直接作为回归损失

但是，IoU无法优化不重叠的b-box情况

本文通过引入一个更一般化的度量方式来作为新的loss和新的度量

本文通过将提出的 $generalizedIoU(GIoU)$ 和已有的 SOTA 算法合并，来测试效果。

引言

b-box 回归是 2D/3D 计算机视觉问题的基础，目标定位、多目标检测、目标追踪和实例分割等都依赖于精准的b-box回归。

目前，在提升应用层面性能的方式是使用更好的backbone[15,13]，或用更好的方式来提取局部特征[6]。忽略了使用 $l_1$ 或 $l_2$ 回归来代替基于 IoU 的回归损失的方式，

IoU 类似于 Jaccard 系数，用于度量两个任意形状的相似程度

IoU 将目标的形状属性（如b-box的宽度、高度和位置等）编码到 region 属性中，然后计算一个基于其面积的标准化度量。

该属性使得 IoU 对目标的尺度具有稳定性

最小化一般的 loss 和提升其 IoU 值没有很强的联系，假设二维情况的例子如图1(a)，其中预测的b-box是黑色框，真实的b-box是绿色框，用（左上，右下）$(x_1,y_1,x_2,y_2)$来表示。为了简化，假设两个b-box的一个corner的距离是固定的（左下），因此，如果预测的第二个角位于以绿色框的第二个角为中心的半径固定的圆上（灰色虚线圆圈），则任何预测的b-box和真实b-box的 $l_2$ 距离将相同。但 IoU 值不同（图1(a)）。图1(b)也一样。

由此可知，这些度量方式的局部最优并不是 IoU 的局部最优，此外，$l_n$ 距离对尺度变化不具有稳定性。一些具有相同重复率但不同尺度的b-box，将会有不同的度量结果。

本文将会研究两个坐标来对齐的矩形的 IoU，该方法具有直观可解释性，与目前一般的观点相反，IoU 可以反向传播，也就是说可以直接将 IoU 作为目标函数来优化。

将优化度量方式和优化损失函数进行对比，最优的方式是使用度量方式本身来进行优化。

但是 IoU 可以作为度量方式，也可以作为损失：如果两个目标没有重叠， IoU 值将为0，无法反映两个形状的距离，如果两个目标无重叠且使用 IoU 作为损失函数，则 IoU 的值为0，梯度为0，无法优化。

本文中，我们将通过扩展到无重叠的情况，来解决 IoU 的缺点。

假设满足以下要求：

• 与一般的 IoU 定义相同，将形状属性编码为区域属性
• 保持 IoU 的形状不变性
• 保证在目标重叠情况下，与 IoU 相关性较强

我们将这个更一般化的 IoU 称为 GIoU，作为衡量两个任意形状的度量，同样地，我们对两个对齐矩形的 GIoU 获得了解析解，允许其可作为损失函数使用。

将 GIoU loss 集成到优异的目标检测算法中，可以提升检测效果。

本文主要贡献如下：

• 提出了一种更 generalized 的 IoU，并作为衡量两个任意形状的度量方式
• 为 GIoU 提供了解析解
• 将 GIoU 和目前流行的目标检测算法集成起来，获得了效果的提升。

2. 相关工作

目标检测准确性度量：

IoU 是目标检测中常用的评估指标，用于确定预测结果中真正例和假正例，使用IoU 作为衡量标准时，需要确定一个阈值。例如在 PASCAL VOC 中，一般使用 mAP，其计算基于固定的 IoU 阈值，如0.5。

任意的 IoU 阈值并不能完全反应某种方法的定位效果，所有高于阈值的框都被认定为同样的质量，为了降低阈值对抑制结果的影响性， MS COCO 数据集将多种 IoU 阈值取得的平均结果也就是 average mAP 作为衡量准则。

Bounding box representations and losses：

2维目标检测中，一个很重要的步骤是学习b-box 的参数，目前已经出现了一些不同的 b-box representations 和 losses 。

YOLO v1 [19] 中提出对有轻微形变的边界框参数直接进行回归的方法，来预测b-box大小的平方根，来弥补尺度敏感性。

[5] 中的 R-CNN 使用选择性搜索方法来预测b-box的位置和偏移量来参数化b-box。为了减轻尺度敏感性，用log域来表示b-box的尺寸和偏移，之后使用 $l_2$ 规范化目标函数，如 MSE loss，来作为优化目标。

[7] 中的 Fast R-CNN 使用 $l_1$ loss 来保证学习过程对异常值更加鲁棒。

[22] 中提出使用一系列的 anchor boxes，之后回归得到预测 b-box 的尺寸和偏移量。但这很难训练，由于正例和负例类别不平衡，为了解决该问题，作者后续提出了focal loss[13] ，该 loss 和本文的落脚点一致。

很多流行的目标检测方法都是使用上述的 b-box 表示方法和损失函数，已经取得了很好的效果。下面将介绍GIoU。

使用近似或代替函数来优化 IoU：

语义分割任务中，一般使用近似的或者代替的函数来优化 IoU。

近期的目标检测任务中，很多方法直接或间接合并 IoU，来更好的执行b-box 回归。但是这些方法在非重叠情况下优化 IoU 时，要么只能得到近似最优，要么会无法得到最优。

本文通过引入 Generalized IoU 来解决 IoU 的缺陷，直接将 GIoU 作为优化目标来训练目标检测问题。

3. Generalized Intersection over Union

IoU 用于对比两个任意形状 A 和 B 的相似度：

$$IoU=\frac{|A\bigcap B|}{|A\bigcup B|}$$

该两个特征在 2D/3D计算机视觉任务中用的很多，如下所示：

• IoU 作为距离来讲（$L_{IoU}=1-IoU$），是一个数学上的衡量标准，也就是说 $L_{IoU}$ 满足非负性、同一性、对称性和三角不等性。
• IoU 对尺度不敏感，意味着两个任意形状的 A 和 B 对其空间尺度不敏感。

IoU 的缺点：

• 如果 $|A\bigcap B|=0$，则$IoU(A,B)=0$。在此情况下， IoU 并不能反映两个形状的距离。
• IoU 无法精确反映两者重合度大小，如下所示，三种情况 IoU 都相等，但其重合度是不同的，左图最好，右图最差。
  

为了解决 IoU 的缺点，本文提出了 GIoU，对两个任意凸面形状的 A 和 B，首先寻找凸面形状 C（包含A 和 B）。如需要对比两个特殊几何形状，那么 C 也是同样的类型的几何形状。如A 和 B 是两个椭圆，C 则是两者交集，也是一个椭圆。之后计算 C 的面积和整个A 和 B 包含的面积的比例。

GIoU 是先计算两个框的最小闭包区域面积，再计算IoU，再计算闭包区域中不属于两个框的区域占闭包区域的比重，最后用IoU减去这个比重得到GIoU，如下所示：

1. GIoU 也是一个距离度量，$L_{GIoU}=1-GIoU$，具有所有的属性，包括非负性、同一性、对称性和三角不等性。

2. 类似于 IoU，GIoU 对尺度不敏感

3. GIoU 永远是 IoU 的下界，$GIoU(A,B)\le IoU(A,B)$，且当 A 和 B 有较强的形状相似性时，该下界更收敛，也就是 $li{m}_{A\to B}GIoU(A,B)=IoU(A,B)$。

4. 与IoU只关注重叠区域不同，GIoU不仅关注重叠区域，还关注其他的非重合区域，能更好的反映两者的重合度。

5. $IoU(A,B)<=1$，而 $-1<=GIoU(A,B)<=1$，具有对称性。

   i) 类似于 IoU，1表示两个形状重合的很完美，也就是 $|A\bigcap B|=|A\bigcup B|$时，GIoU=IoU=1。

   ii) 当两个形状的重复ratio $|A\bigcup B|$ 和 $|C|$ 的面积接近于0时，GIoU 的值接近-1。也就是$li{m}_{\frac{|A\bigcup B|}{|C|}\to 0}GIoU(A,B)=-1$

总之，该一般性保留了 IoU 的主要特征，同时避免了其缺点，因此，GIoU 可以在2D/3D 计算机视觉任务中适当地代替 IoU 来衡量距离。

本文主要研究2D 的目标检测，可以简单的获得 GIoU 的解析解，故可以将其作为距离度量和损失度量。

3.1 GIoU as Loss for Bounding Box Regression

IoU 没有解析解，无法直接作为损失函数来优化，

2D 目标检测是对比两个坐标对齐的的任意形状的距离，GIoU 可以直接得到其解析解，该情况下，重叠部分和最小的闭包目标都是矩形形状，可以看出，它们顶点的坐标仅仅是被比较的两个边界框中的一个的坐标，这可以通过使用min和max函数比较每个顶点的坐标来实现。要检查两个边框是否重叠，还必须检查一个条件。因此，我们有一个解析的解来计算IoU和GIoU。

因为背景是 min，max 和逐块的线性函数，如Relu 和 feasible，Alg2 中展示了，每个模型都有很好的表现。因此，IoU 或 GIoU 都可以被作为损失函数，如 $L_{IoU}$ 或 $L_{GIoU}$ ，来优化目标检测的网络。

• 分别计算 gt 和 predict box 的面积
• 计算交集面积
• 计算最小闭包面积
• 计算 IoU 和 GIoU
• 根据公式得到 loss

此情况下，我们直接优化距离来作为损失，该损失是最优的形式，然而，对于不重叠的情况， IoU 的梯度为0，这会影响训练过程和收敛速度，包括无重叠情况。

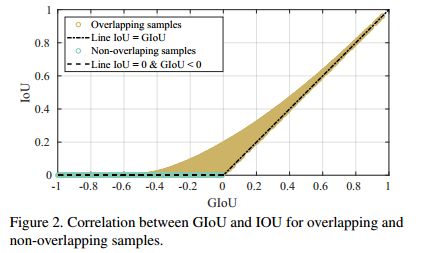
另外，使用 property 3（下界的那个关系），可以发现 GIoU 和 IoU 有着很强的关联，尤其是在 IoU 的值较大的时候，我们在图2 中呈现了这种关系，使用10k 个随机样本。

图2中，我们观察到在重复率较低情况下， 如 IoU <=0.2，GIoU<=0.2，GIoU有能力比 IoU 获得更多的变化，结尾处，GIoU 可能比 IoU 的梯度更加陡峭，所以将 GIoU 作为 loss 比使用 IoU 更好。

Loss Stability：

本文研究了如果存在极端的情况，会否使得 loss 不稳定或不明确，如何确定输出值。

假设gt box $B^g$是一个矩形区域，其面积大于0，那么 $A^g>0$。

Alg.2(1) 和 Alg.2(4) 分别确定了预测区域 $A^p$ 和重叠区域 $L$ 都是非负的，即 $A^p>=0,L>=0$。所以对所有的预测值 $B^p=(x_1^p,x_2^p,y_1^p,y_2^p)\in R^4$，都有 union $u>0$。

这就保证了对于所有的预测输出， IoU 的分母不会为0，此外，对任何值 $B^p=(x_1^p,x_2^p,y_1^p,y_2^p)\in R^4$，union 都大于交集面积，也就是 $u>=L$。因此，$L_{IoU}$ 总是有上下界的，也就是$0<=L_{IoU}<=1$。

为了验证 $L_{IoU}$ 的稳定性，额外的一项 $\frac{A^c-u}{A^c}$ 应该被预定义为一个确定的值。

所有预测的值的最小闭包 $B^c$ 不会比$B^g$还小，所以 $\frac{A^c-u}{A^c}$的分母总是一个正的非零值，因为 $A^c>=A^g$，且 $A^g>=0$。

此外，所有预测得到的最小闭包不会小于 union，也就是 $A^c>=u$。故 GIoU 的额外一项是正的且有界的，因此， $0<=L_{GIoU}<=2$。

当 IoU=0 时，$L_{GIoU}$的特点：

对于 GIoU loss，我们有 $L_{GIoU}=1-GIoU=1+\frac{A^c-u}{A^c}-IoU$，当 $B^g$ 和 $B^p$ 没有重叠时， $L=0$ ，$IoU=0$，GIoU loss 简化为$L_{GIoU}=1-GIoU=1+\frac{A^c-u}{A^c}=2-\frac{u}{A^c}$。

该情况下，为了最小化 $L_{GIoU}$，需要最大化 $\frac{u}{A^c}$，该项被规范化到0~1之间，也就是$0<=\frac{u}{A^c}<=1$。当最小闭包 $A^c$ 最小的时候，该值最大，且 $u=A^g+A^p$，更精确的说，也就是预测的b-box $A^p$ 是最大的。

为了实现该目标，预测的 b-box $B^p$ 的最高点，应该移动到一个方向，来促进 $B^g$ 和 $B^p$ 的重叠，保证 IoU 不等于0。

4. 实验

通过将本文提出的GIoU loss 和已有的 Faster R-CNN 、Mask R-CNN 和 YOLOv3等网络的结合，来探究本文网络的的效果。

我们将其原有的 loss 使用 $L_{GIoU}$ 来替换，也就是替换 Faster/ Mask R-CNN 中的 $l_1$ 损失，替换 YOLO v3中的 MSE 损失，同时对比了最终结果。

数据集：

PASCAL VOC[4] 和 MS COCO[14]。

PASCAL VOC 2007： Pascal Visual Object Classes（VOC）基准是分类任务、分割任务和目标检测任务的应用很广泛的数据集。包括 9963 个图像，训练和测试各占一半，20个预定义的类别都有b-box 标注。

MS COCO： 包括多于 200000 个图像，用于训练，验证和测试的数据集多于 500000 个标注好的实例，共80个类。

实验细节介绍：

使用不同 IoU 阈值所得到的类间的 mAP 来衡量真阳性和假阳性。主要使用 AP 来衡量该基准数据集的性能，之后将不同 IoU 阈值情况下所获得的 mAP 的均值来作为衡量标准，包括 IoU ={0.5,0.55,…,0.95}等。

此外，使用 GIoU 来修正评估结果，来确定其真阳性和假阳性。因此，我们使用 mAP 的均值来作为衡量AP 的一个值，当阈值为0.75时，表中表示为 AP75。

4.1 YOLO v3

训练过程：

此处使用原始的 Darknet 实现的 YOLO v3，对于基准结果（使用 MSE loss 训练的），我们使用 Darknet-608 作为backbone网络，并且使用基准参数。

为了分别训练基于 IoU 和 GIoU 的 YOLO v3，我们直接利用 IoU 和 GIoU 来代替 MSE 。

考虑到分类需要额外的 MSE loss ，且由于我们使用有界的距离损失来代替无界的距离损失，我们需要调整新的b-box回归来解决分类损失。我们使用了一个非常小的变化来调整回归 loss 来应对 MSE 分类损失。

1）PASCAL VOC 2007：

遵循原始网络的训练过程，我们在训练集和验证集上使用每种 loss 来训练网络，迭代次数大于50K，如表1所示。

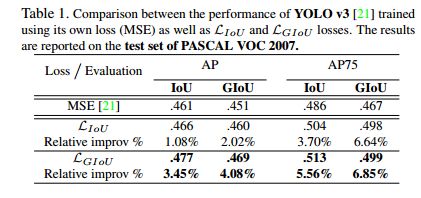
对比标准 IoU 和新的 GIoU 的效果，从表中可知，使用 $L_{GIoU}$ 作为回归损失时比使用 MSE 作为回归损失的效果好。

2）MS COCO 数据集：

遵循原始网络训练方法，使用所有的训练集和 88% 的验证集来进行约502k次的训练，之后，我们使用剩余的 12% 的验证集得到的结果如表2所示。

同样在 MS COCO 2018 数据集中也进行了实验，结果见表3.

图3（a）中展示了使用 $L_{GIoU}$ 时， YOLO v3的定位准确性有所提高。

由于目前对正则化参数进行了简单的调优，平衡了边界框损失和分类损失，但与基准结果相比，分类得分可能不是最优，如图3（b）。

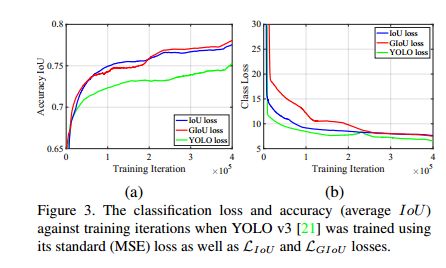
由于基于 AP 的性能度量受到分类误差的影响较大，我们认为通过寻找正则化参数可以进一步改善结果。

4.2 Faster R-CNN and Mask R-CNN

训练过程：

对于基准过程（使用 $l_1$-smooth），本文使用 RestNet-50 作为 Faster R-CNN 和 Mask RCNN 的 backbone，参数都使用默认参数。

分别使用 GIoU 和 IoU 对两个分割网络进行训练，也就是利用 $ L_{IoU}$ 和 $L_{GIoU}$ loss 代替 $l_1$-smooth loss 进行训练，如 Alg.2 所示。

类似于 YOLO v3，我们对新的回归损失进行了最小的调整，使之与分类和分割损失等其他损失相对应，我们只是简单地将所有实验的 L_{IoU}$ 和 $L_{GIoU}$ 乘以10。

PASCAL VOC 2007：

由于该数据集中没有实例mask的标记，所以无法在该数据集上测试 Mask R-CNN 的效果，因此仅仅对 Faster R-CNN 进行测试，见表4。

使用 $L_{GIoU}$ loss 比使用 $l_1$-smooth loss 的效果更好，此外，将 $L_{IoU}$ loss 合并到回归损失中后，可以对 Faster R-CNN 的基准性能略有提高，但比使用 $L_{GIoU}$ loss 带来的提升略差，如图4，IoU 的阈值从 0.5~0.95。

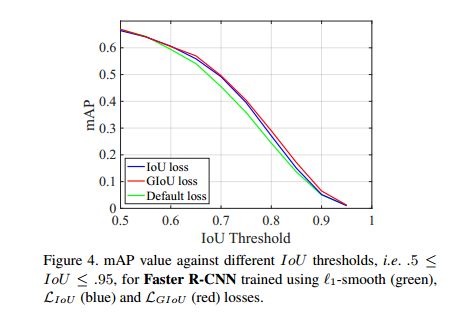
MS COCO：

在 MS COCO 2018 训练集上训练了 Faster R-CNN 和 Mask R-CNN，迭代次数为95k，验证集上的结果分别见表5和表7。

在 MS COCO 2018 challenge 测试的结果见表6和8。

$L_{GIoU}$ 作为 loss 的检测效果优于 $l_1$-smooth，然而其提升的数量低于之前的实验，其原因有很多：

• 首先，Faster R-CNN [22] 和 Mask R-CNN [6] 的anchor box 比 YOLO v3 的更加密集，导致 GIoU 相对于 IoU 的优势场景不太常见，如不重叠的边界框。

• 其次，在 PASCAL VOC 上对b-box 的正则化参数进行了简单的调优，在 MS 上得到了次优的结果。

5. 结论

本文提出了GIoU 作为新的度量方式，来衡量两个任意形状的距离，能够克服 IoU 的缺点。

同样，我们对两个坐标对齐的矩形的 GIoU 提出了解析解，GIoU 作为距离度量，其导数可以计算出来，故 GIoU 可以被作为 b-box 的回归损失。

通过将该损失应用于目前先进的目标检测方法中，对其性能都有了一定的提升，如在 PASCAL VOC 和 MS COCO 等数据集上都有效果的提升。

由于最优损失函数就是该度量标准本身，所以 GIoU 损失可以作为最优 b-box 回归损失。

未来，我们可以研究在两个可旋转的矩形的 GIoU，可以用于3D 目标检测框架。