3D点云重建0-03:MVSNet-白话给你讲论文-翻译无死角(1)
以下链接是个人关于MVSNet(R-MVSNet)-多视角立体深度推导重建 所有见解,如有错误欢迎大家指出,我会第一时间纠正。有兴趣的朋友可以加微信:a944284742相互讨论技术。若是帮助到了你什么,一定要记得点赞!因为这是对我最大的鼓励。
3D点云重建0-00:MVSNet(R-MVSNet)–目录-史上最新无死角讲解:https://blog.csdn.net/weixin_43013761/article/details/102852209
前言
在进行论文翻译和讲解之前,我要给大家说清楚一些事情MVSNet(2018),R-MVSNet(2019)分别各自都对应有自己的论文,也就是有两篇,我首先为大家讲解的是第一篇,也就是MVSNet,后面再给大家讲解R-MVSNet。那么我们就开始把。
摘要
他讲他们提出了一种,从多个视觉图片进行深度图推导的方法,并且可以进行端到端的学习训练。再这个网络中,他们首先从输入图像提取特深度图特征,然后结合多个稍微有点不同的,单应性锥形特征图去构建3D cost volume(这里保存的信息,主要是视觉差的信息),下面就是对这个立体特征进行3D卷积,让立体特征更加有序,并且生成最初始的深度图。然后结合参考图片(输入图片中特定的一张-后续讲解),对初始深度图进行优化,提纯。
我们的框架可以支持任意张,不同视角图片的输入,主要是因为使用了一种方差成本度量的方法(原来就是利用视觉差,计算视觉损耗-后续讲解)。大量的实验证明MVSNet的泛化能力很强,只需要简单的后期处理,不仅超越了最先进的方法,并且速度也比他们快很多倍。
1、介绍
Multi-view stereo (MVS) -多视角立体深度估算,近十年来都有很多人对其进行了研究。比如传统的方法 ,是通过手工精心的去做出相似的指标,或者设计相关规则(如标准化交叉相关,局部-全局匹配),然后计算出高密度的3D点云之间的关系。这些方法,在理想的场景下展现出很高的准确率,但是他们都有一个共同的局限性,容易受到低纹理,反光和局部反射的干扰,导致匹配很艰难,从而造成重构的3D立体或者深度图不完整。虽然现在有的算法,在准确率上已经很高了,但是在重构完整性这个方面,还有很大的改善空间。
最近,神经网络的出现,引起了很多人对立体重构改善的兴趣。理论上来说,深度学习的方法带有全局的语义信息,让他学习到高光,或者反射的信息,以至于更好的去进行2维到3维的匹配。也有一些使用两个视觉图,代替手工合成相似标准的方法,去进行立体匹配(基于深度学习)。这种方法展示出令人满意的结果,并且慢慢的超出了传统的方法。在实际中,神经网络是完全使用于立体匹配的,在图片送入网络之前,我们先对其进行矫正,这样就能让图片水平了,避免摄像头偏转,等其他不一致信息的干扰。
然而,想把两个视角立体图扩展到多个视角的立体图,并不是一件简单的事情。虽然我们可以,使用两两配对的方法,如每两张视角图都分成一个对,然后进行融合,再去重构一个完整的3D点云。但是这样,会丢失很多视角之间联系的信息,从而导致准确率不高。
与立体匹配不同的是,MVS可以输入任意几何空间形状的图片,这对于研究来说,是一个比较棘手的问题,只有少数的学者注意了这个问题,并且使用CNN对其进行MVS重构,如SurfaceNe构建Colored Voxel Cubes (CVC-立体颜色像素),这个网络的输入,融合了所有输入图片的像素,以及相机的信息。与之相反,Learned Stereo Machine(LSM)直接采用了端到端学习的方法。但是他们两种方法,都是使用了规则的网格表示,这样他们的受到内存的限制,网络的构建不能太大:LSM使用手工进行合成,并且立体分辨率也非常的低。SurfaceNet是采用了一种分割的办法,但是这样重构会花费很长的时间。到了目前,能够是MVS达到高准确率的,还是传统方法。
但是,我们针对深度图推导提出了一种端到端学习的算法,他是每次计算一个深度图,并不是一次输出整个3D场景。该算法的输入是一张reference image(后面称呼为r img )和几张source images(后续称为s img),然后去推断r img 的深度图。这其中的关键在于differentiable homography(有细微差距的同形状,不同意义的矩阵)的扭曲映射的操作,它会把对摄像头图片隐含的几何信息进行编码,把2D的特征图映射到一个3D cost volumes,并且这个过程是可以进行端到端的训练的。
为了使用任意数量的s img输入,我们提出了一种基于方差度量的方法,把多个features 映射到一个 cost feature volume。这个cost volume通过多个3D卷积得到一个初始的深度图。最后这个初始深度图(initial depth map)和r img共同作用,去改善边界范围的准确率。我们的方法和之前的方法,主要两个不同点。
1.对于深度图的推导,3D cost volume是建立在,一个摄像头锥形特征(后面的图示我们能明显的看到)代替欧几里和空间的基础上。
2.将MVS重构分解成了更小的深度图估算,这样就为大迟度重构提供了可能。
我们提出MVSNet的训练和评估都是基于大尺寸的DTU数据集,大量的实验证明(我们的方法带有少量的后期处理),其超出了所有竞争方法,无论是在重构的完整性和质量上。除此之外,在Tanks 和Temples数据集上,还体现了很好的泛化能力,在速度上也完全胜出当前先进的一些算法。
2、相关工作
MVS Reconstruction. 从输出的结果来看,MVSNet网络有以下几种功效:
1.直接进行点云重构
2.重构立体重构
3.重构深度图
基于点云的方法,对3D点云进行操作,通常依赖于传播策略逐渐增大密度进行重建。由于点云得传播都是逐步进行的,所以不能并行,导致重建需要花费很长的时间。
基于体积的方法,是把3维空间划分中多个规则的立体像素网格,然后估算每个立体像素是否粘附在表面。他的缺点主要是空间离散度误差,以及巨大的内存消耗。
相比上面的方法,深度图的表示更加灵活,将复杂的MVS重建,转化为简单深度估算。在一次运算过程中,只需要一张r img和几张s img即可。并且深度图能够很容易的融合到点云上,或者3D体积上。目前最好的MVS算法,也是基于深度图实现的。
**Learned Stereo.**相比于传统手工提取的图片特征,进行匹配。基于深度学习的方法更加好。Han等人,首先提出了匹配两层不同图像的网络(应该类似与图片拼接),Zbontar和Luo利用学习到的特征进行立体,或者全局匹配(带有一些后期处理),其超过了图像成对匹配的方法,并且这种技巧也被用在了立体成本计算上面。目前最先进的方法是GCNet,他是通过3D卷积调整cost volume,并且通过soft argmin缩小差距。他时学习多个视角图,然后进行端到端的训练,其算法很明显的超过的传统的算法。
Learned MVS 有一些尝试学习MVS(多视角立体估算)的方法,如Hartmann提出了多个视角差去代替传统计算cost 的方法。SurfaceNet时第一个针对于MVS学习的网络,其使用复杂的体素计算得到cost volume,然后使用3D卷积推导表面体素。与我们提出方法比较相近的是LSM,其会在网络中对摄像头参数进行编码,然后形成cost volume,3D卷积是要用于体素分类,其分类的标准为是否依附在物体表面。使用3D体积表示,他们(SurfaceNet和LSM)有一个共同的缺点,那就是只能对小分辨率的图像进行重构。当然他们也使用了分割-重构的策略。但是这样延长了时间,但是我们提出的方法,每次都是推导处r mg的深度图,这样我们能够对比较大的场景进行重构。
3、 MVSNet
这里主要是对我们提出的网络框架MVSNet进行详细的描述,MVSNet的设计严格遵循了摄像头物理集合的规律,并且结合前人对MVS的讲解。后面就是我们的网络和一些传统方法的对比,大量的实验证明,我们的算法在MVS方面是最先进的,MVSNet的网络架构如下所示:
Fig. 1
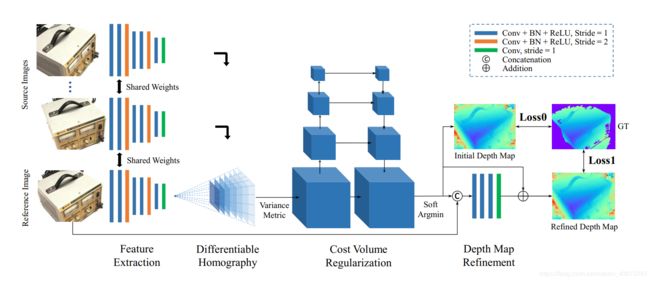
图像描述:这是MVSNet网络的结构,输入图像经过二维特征抽取,以及不同的单应性变换,然后映射到cost volume。最终的深度图,是从经过正则化的概率图以及与r img进行提炼获得。
该 处 接 下 的 都 为 重 点 , 请 大 家 认 真 琢 磨 \color{#FF0000}{该处接下的都为重点,请大家认真琢磨} 该处接下的都为重点,请大家认真琢磨
3.1 Image Features
MVSNet的第一步是对每张输入图像 { I i } i = 1 N {\{I_i\}_{i=1}^N} {Ii}i=1N进行特征提 { F i } i = 1 N {\{F_i\}_{i=1}^N} {Fi}i=1N取,N表示输入图像的总张数。其提取过程,是8层的卷积网络,在第3层和第6层把strides设置为2,让特征图经过两次缩放,形成3个尺寸的特征图。对于每个尺寸,都使用了两个卷积,去提取更高级的图片特征。除了最后一层卷积,其他层都带有BN正则化以及ReLU激活。与场景的匹配任务类似,为了高效的学习,他们的权重都是共享的(即提取张图片的特征,使用的都是同一个网络)。
这个2D网络输出的特征图是N(输入图片数目)个32通道的特征图,与输入图像相比,长宽都缩小的4倍(经过两次strides=2的缩放)。所以这个地方大家注意一下,图片经过特征抽取之后,尺寸已经变小了,所有图片的像素信息已经被编码到了这个抽取出来的特征图之中,这样是为了再进行密度匹配的时候,丢失比较重要的上下文信息,相比于使用原图进行密度匹配,这种方法很明显提高重构的质量(5.3有详细的介绍)
3.2 Cost Volume
下一个步骤,就是利用摄像头参数和对应图片抽取出来的特征图 去构建3D cost volume(下图框出部分)
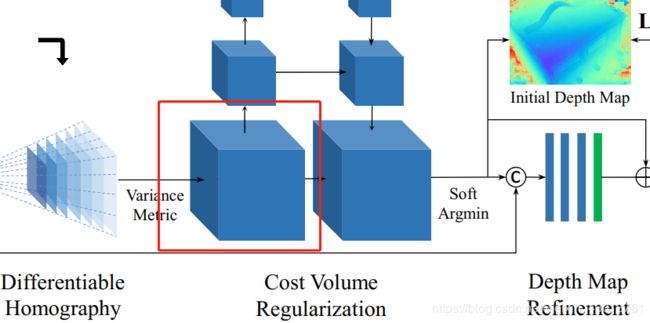
之前的一些方法,会把这个空间分割成规则的立体网格。但是我们对深度图的推导,构建cost volume都是建立在参考摄像头(拍摄r img图片的摄像头)的锥形原理之上。为了简单起见, 接 下 来 使 用 : \color{red}{接下来使用:} 接下来使用:
I 1 I_1 I1表示 r img图像
{ I 2 } N \{I_2\}^{N} {I2}N表示 s img图像,注意,可能存在多张s img图像。
{ k i , R i , t i } i = 1 N {\{k_i, R_i, t_i\}}^N_{i=1} {ki,Ri,ti}i=1N表示一个内联函数,即s img抽取出来的特征通过旋转,平移,变换成r img抽取出来特征的公式。
Differentiable Homography这里涉及到了一个概念,就是Homography,首先可以看看这篇博客:
单应性矩阵的理解及求解:https://blog.csdn.net/liubing8609/article/details/85340015
其原理是什么呢?通过前面我们知道,r img经过2D特征提取,得到r feat(个人缩写,大家能明白就好了),s img经过2D特征出去得到s feat。其中他们每张图片的视角都是不一样的,现在呢,但是我们求的深度图,仅仅是r img图像对应得深度图,所以我们要把s img得视角,通过单应性变换,转换为r img的视角。单应性变换,就把一个视角转换为另外一个视角。
所有的s img的特征图,都通过单应性变换,把视角转换到r img对应的立体空间。 N张映射过来之后的特征图形成feature volumes { V i } i = 1 N {\{V_i\}^N_{i=1}} {Vi}i=1N,也就是下图中的这个:

映射过来之后的特征图在深度d处的哪个位置(也就锥形的中的第几个特征),由公式 x ′ x' x′ ~ H i ( d ) ⋅ x H_i(d)·x Hi(d)⋅x决定,也就是说上图中, F i F_i Fi映射成Vi(d)之后,其深度的坐标,可以通过 x ′ x' x′ ~ H i ( d ) ⋅ x H_i(d)·x Hi(d)⋅x计算获得。这里的 ‘~’ 符号表示为深度同等映射, H i ( d ) H_i(d) Hi(d)表示s img映射到r img图像对应的锥形的空间的深度。让拍摄r img的摄像头作为主轴,单应性转换关系,可以用一个3X3的矩阵表示(我晕,真的好难翻译,我感觉翻译不过来,我们到源码取找答案吧)。
H i ( d ) = K i ⋅ R i ⋅ ( I − ( t 1 − t 2 ) ⋅ n 1 T d ⋅ R 1 T ⋅ K 1 T ) H_i(d) = K_i·R_i·(I-\frac{(t_1-t_2)·n_1^T}{d}·R_1^T·K_1^T) Hi(d)=Ki⋅Ri⋅(I−d(t1−t2)⋅n1T⋅R1T⋅K1T)
一般情况下,r feat map F 1 F_1 F1他有一个标识自己的3x3矩阵,这个扭曲(warping)的过程有点类似于平面扫面立体,除此之外,可微线性插值用在特征图 { F i } i = 1 N {\{F_i\}_{i=1}^N} {Fi}i=1N上,比直接用在输入图像 { I i } i = 1 N {\{I_i\}_{i=1}^N} {Ii}i=1N上要好。这里的线性插值可以理解为warping(扭曲)的操作,可以通过微分,分步骤实现。
本 人 理 解 , 仅 供 参 考 , 一 切 源 码 为 主 \color{red}{本人理解,仅供参考,一切源码为主} 本人理解,仅供参考,一切源码为主
大家看了翻译可能比较懵逼,现在我大概的猜测一下(实际还是得根据源码来,后续会进行分析):
就是说,对输入的r img以及s img经过特征提取后,得到特征图 { F i = 1 N } {\{F_{i=1}^N\}} {Fi=1N}( F 1 F_1 F1表示r img的对应的特征图,其余表示s img的特征图)。他们的维度是相同的,但是经过经过Homography变换之后,把s img的特征图,映射到r img的特征图对应的锥形立体空间之后,由于深度不一样,形成上面红框的锥形(长宽也不一样)。然后对锥形的每个特征图进行线性插值,让他们长宽相同。这里是一个比较重要的过程,因为这里完成的2D到3D的转换,让3D端到端的训练成为了可能。
Cost Metric 下一步,我们将合并多个feature volumes { V i } i = 1 N {\{V_i\}_{i=1}^N} {Vi}i=1N为一个cost volume C,为了适应任意数目的视角输入,我们提出了一种基于方差的c ost计算方式。用W,H,D,F表示宽,高,视觉图的数目,通道数。 V = W 4 ⋅ H 4 ⋅ D ⋅ F V=\frac{W}{4} ·\frac{H}{4}·D·F V=4W⋅4H⋅D⋅F表示特征图的体积大小。 cost的映射关系如下:
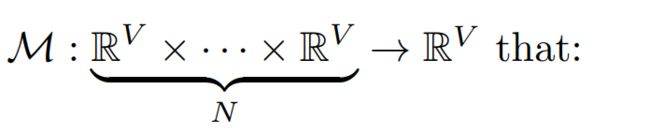
c = M ( V 1 , ⋅ ⋅ ⋅ , V N ) = ∑ i = 1 N ( V i − V i ‾ ) 2 N c = M(V_1,···,V_N)={\frac{\sum_{i=1}^N(V_i-\overline{V_i})^2}{N}} c=M(V1,⋅⋅⋅,VN)=N∑i=1N(Vi−Vi)2
这里的 V i ‾ \overline{V_i} Vi是所有feature volumes中的平均feature volume。
在最好的传统方法中,计算cost 是使用r img与多个s img通过两两配对进行计算,我们也使用了这种方法。在计算的cost 的时候我们应该遵循这样的原则,不能偏向侧重于r img的cost,我们应该对每个输入的视觉图都平等对待。我们注意到,最近的一些方法,使用多层CNN网络进行多个视角平均推导。我们这里只用方差代替了平均值,因为均值操作本身没有提供关于特征性差异的信息。并且他们的网络在推导相似点的时候需要前期以及后期处理,但是我们的是基于方差计算的,以及很明显得或者了视觉差异性得信息,所以不需要做那些处理。后面我们用实验证明给出了这个结论。
Cost Volume Regularization 最初始形成了cost volume,即如下红框中的部分:

他是带有很多噪声的,比如存在非朗伯曲面或者遮挡等。所以应该结合平滑度对深度图进行约束。所以我们在cost volume C的基础上,去生成一个probability volume P,用于深度图的推断。受到基于深度学习以及传统MVS做法的影响,我们采用了多尺度3D CNN对cost volume进行规则化,在该网络中,有四个缩放的尺寸,有点类似于3D版本的UNet,其采用编码-解码的架构,使用较小的内存,去合并周边的信息。为了进一步减少内存的消耗,在第一个3D卷积之后我们把32通道的cost volume减少到8个通道,并且在第2层和第3层缩小得图片的尺寸。最后的3D卷积层输出一个单通道的volume,最后我们利用深度方向的softmax操作进行概率归一化。
最后得到的是probability volume(该体素存储的是r img图像,在该立体空间的的深度概率值),如下红框部分:
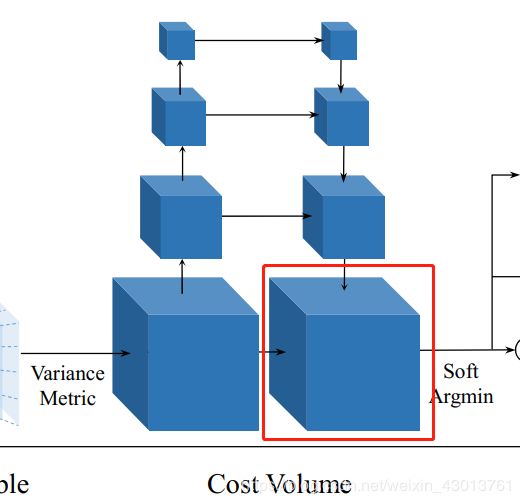
我们实验中,得到的probability volume效果比较好,他不仅仅可以用于每个像素深度的估算,也可以用来标志测量估算的置信度(后面会有详细的介绍)。通过重建概率的分布,能很容易的分析出重构的质量怎么样,这里引入了一个对离群点进行过滤的方法(后面有介绍)。
3.3 Depth Map
Initial Estimation 从probability volume P去获得深度图,是最简单的一种方法,但是如果使用argmax 方法(probability volume P选取概率最大的体素),我们就不能对其他的体素进行深度评估,并且由于其不可微分(比较懵逼),所以不能进行反向传播。所以我们计算深度方向的期望值,也就是他们概率权重的所有和:
D = ∑ d = d m i n d m a x d × P ( d ) D=\sum_{d=d_{min}}^{d_{max}}d \times P(d) D=d=dmin∑dmaxd×P(d)
这里的 P ( d ) P(d) P(d)是所有体素在深度d上概率估算,注意,这个操作也涉及到了soft argmin 操作。他是可微分的,并且结果十分接近argmax的结果。对于每个样本来说,他们构建cost volume,对深度进行估算的最大值和最小值 [ d m i n , d m a x ] [d_{min},d_{max}] [dmin,dmax]都是不一样的,所以希望能有一个连续估算的值产生。输出的深度图如下Fig. 2 (b),他的大小和2D的特征图大小是一样的,相比如输入图像,其缩小了四倍。
Fig. 2

图描述:这是表示的分别是原图,初始深度图,概率描述,以及概率图。(a)来自DTU数据集,一个扫描得到r img。(b)推断出来的深度图。©上图表示没有离群的像素,下图表示离群的像素,其中假设x轴的是深度坐标,y轴是这个体素在这个深度的概率值。(d)这个图是图(b)概率图,以为离群点是比较分散的,所以被计算的概率也比较低。
Probability Map
沿深度方向的概率分布也能体现出图深度图的质量,虽然多尺度3D CNN(就是前面类似于3D版本的UNet),具有很强将概率正则化为单模态分布的能力,但是我们注意到,对于那些匹配错误的像素,他们在深度方向的概率分布是比较离散的,没有办法集中,如下:
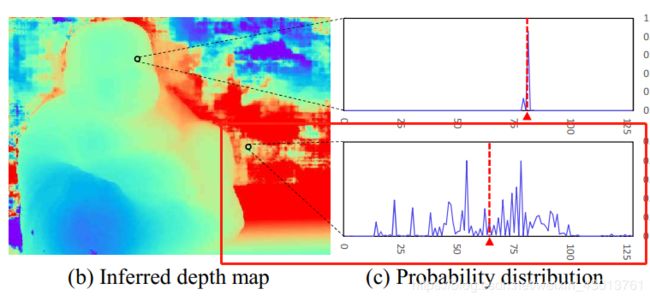
基于这种观察,我们使用 d ‾ \overline{d} d去代替一个小范围的深度概率。前面我们深度的采样,是基于锥形摄像头的原理,我们简单的去4个深度范围的体素概率值,来衡量这个深度估算的质量(具体做法,在后面源码分析中做具体介绍)。当然还有一些其他的统计测量方式,比如标准差和熵的方法,都能在这里使用,但是在我们实验的过程中发现,其不能很多好对深度图进行过滤,所以我们的方法能够更好的对离群点进行过滤。
第一次接触3D,所以翻译得不是很好,希望大叫不要介意,在源码分析的过程中,我会讲解每一个细节,今天到这里吧,剩下的明天为大家翻译完,再见了,老铁!