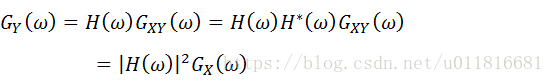统计信号处理课程学习笔记

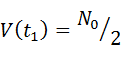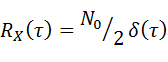白噪声：函数均值为0，相关函数RXt1,t2=Vt1δt1-t2的随机过程为白噪声。其中Vt1是任意非负函数。如果Vt1=N02，则称Xt为平稳白噪声，即有RXτ=N02δτ，PXω=N02。

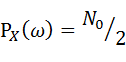有色噪声：功率谱不是常数的噪声。

正态随机过程：任意N维分布都是正态分布的随机过程。pX=12πN2CX12exp-12X-mXTCX-1X-mX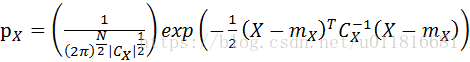

 

线性变换：设Yt=LXt，如果LA1X1t+A2X2t=A1LX1t+A2LX2t，其中A1，A2是随机变量，X1t，X2t是随机过程，那么成L为线性变换。改变换满足齐次性、可加性。若Yt+ε=LXt+ε，则称该线性变换L为线性时不变变换。

变换的基本定理1：EYt=LEXt

变换的基本定理2：RXYt1,t2=Lt2RXt1,t2

变换的基本定理3：

RYt1,t2=Lt1RXYt1,t2=Lt1∙Lt2RXt1,t2

变换的性质：输出的k阶矩有输入的k阶矩确定，输出的平稳性取决于输入的平稳性。

 

随机过程通过线性系统时域法：Yt=ht*Xt，Xt是输入的随机过程，Yt是输出的随机过程，ht是线性系统的冲激响应。适用于平稳过程、非平稳过程。

性质1：mYt=EYt=Eht*Xt=ht*EXt，当输入随机过程是平稳的，EXt=mX是一个常数，那么mYt=-∞∞mX∙ hτdτ=mX∙H0，其中H0是系统传递函数Ht|t=0。

性质2：RXYt1,t2= ht2*RXt1,t2

性质3：RYXt1,t2= ht1*RXt1,t2

性质4：

RYt1,t2= ht1*RXYt1,t2=ht1*ht2*RXt1,t2

性质5：当Xt平稳时，RXYt1,t2=ht2*RXt1,t2=-∞∞RXt1-t2+u∙ hudu= h-τ*RXτ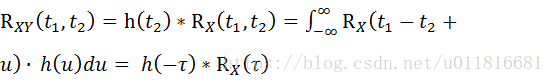

随机过程通过线性系统频域法：分析输入输出的功率谱，简化计算。当Xt平稳时，

GYω=HωGXYω=HωH*ωGXYω=Hω2GXω

因为频谱法利用了相关函数与功率谱是傅里叶对的性质（即维纳－辛钦定理），所以频谱法只适用于Xt平稳的条件。

典型随机序列的模型：许多随机序列可以看成由一个白噪声序列激励一个线性系统所产生的，一般表示为k=0NX[n-k]∙ak=l=0MW[n-l]∙bl，其中W[n]是零均值、方差为σ2的平稳高斯白噪声，a1=1，b1=1。称该模型为ARMA模型。