【机器学习】到底什么是交叉熵

一般地，熵(Entropy)被用于描述一个系统中的不确定性(the uncertainty of a system)。在不同领域熵有不同的解释，比如热力学的定义和信息论也不大相同。

要想明白交叉熵(Cross Entropy)的意义，可以从信息量 -> 熵 ->相对熵-> 交叉熵这个顺序入手。

---

信息量

顾名思义信息量表征事件发生冷门程度，越冷门，信息量越大。举个栗子，当小概率事件发生时，提供的信息量往往很大，或者说令人惊讶，例如中国男足勇夺世界杯冠军因为概率很小趋近于0，所以当该事件发生时提供的信息量就很大趋近于，反之中国乒乓球包揽金牌，该事件概率很大趋向于1，那么信息量就很小趋近于0。

      

import matplotlib.pyplot as plt
import numpy as np

x=np.linspace(0,6,1000) #创建100个0到6之间的等比数列

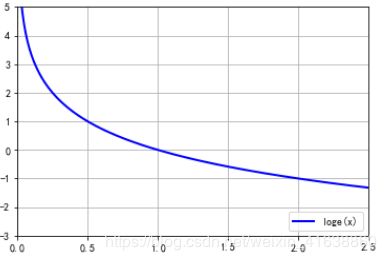
plt.plot(x,-logn(2,x),'b-',linewidth=2, label=u'loge(x)') #loge(x)
plt.axis([0, 2.5, -3., 5.]) #指定画图板的长宽
plt.legend(loc = 'lower right') #图例的位置
plt.grid(True) #需要网格
plt.show()

 

补充:实际上,log的底可以是其他的数字，常用的是2和e这两个底。底是2的时候,单位为bit。.底是e的时候,单位为nat。

---

熵

所有可能结果的信息量的总和组成熵

   

举个例子：

中国队vs巴西队，假设中国队的胜率是0，巴西队胜率是1,可知：

H(巴西队)=赢球的信息量+输球的信息量=1×-log1+0×-log0 = 0

荷兰队vs巴西队，假设荷兰队和巴西队的胜率都是0.5，可知：

H(巴西队)=赢球的信息量+输球的信息量=0.5×-log0.5+0.5×-log0.5= 1

综上易知，熵表征的是期望的稳定性，值越小越稳定，当熵为0时该事件为必然事件，熵越大表示该事件的可能性越难以估量。

---

相对熵（KL散度）

其中p(x)，q(x)为同一随机变量两个独立的概率分布。举个栗子，在机器学习的问题中常用p(x)表示label，q(x)表示predict值，如p(x)=[1，0，0]表示该样本属于第一类，q(x)=[0.9，0.3，0.2]表示预测该样本有0.9的概率属于第一类，显然这里用p(x)来描述样本是十分完美的，而用q(x)描述样本只能得到一个大致的描述，不是那么完美，缺少了一些信息量。经过反复的训练最后q(x)=[1，0，0]即可以完美描述该样本则，DKL=0。

在一定程度上面，相对熵可以理解为两个随机变量之间的距离。当两个随机分布相同的时候，他们的相对熵为0，当两个随机分布的差别增大的时候，他们之间的相对熵也会增大。 但这样的理解是不够准确的，因为相对熵是不具有对称性的，回顾一下条件概率的公式：

显然

在机器学习中，我们常将相对熵（交叉熵是相对熵的一部分）定义为损失函数loss，我们train的目标就是要minimize(loss),其中为p(x)真实的标签，q(x)为预测值。基于以上将相对熵定义为，q(x)刻画p(x)的难易程度，即为其值越小则q(x)刻画p(x)越简单，当相对熵为0时，预测值完美刻画真实样本。

---

交叉熵

什么是交叉熵

交叉熵主要用于度量两个概率分布间的差异性信息

回顾一下相对熵的公式

我们都知道 

则  

其中熵的定义为：

显然

我们将公式的后半部分称之为交叉熵定义为：

---

机器学习中为什么选择交叉熵作为损失函数

在机器学习中，终极目标是让我们训练的模型学习到真实数据的数据分布，即。

但是真实的数据分布是不可知的，我们只能用所获得的部分训练数据近似的代替真实数据的数据分布

即将训练数据作为模型和真实数据分布的介质，则有。

根据上文我们知道衡量两种概率分布之间的差异性非常可行的方法就是用计算它们的相对熵。

显然在训练模型的过程中是保持不变的，求相对熵最小就等价于求最小。

当交叉熵最低时(等价于训练数据分布的熵)，我们学到了“最好的模型”。

所以一般在机器学习中直接用交叉熵做为损失函数loss，以用来评估模型的好坏程度。