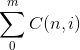@HDU 6333 @HDU多校第四场:Problem B. Harvest of Apples (分块思想)

 

Time Limit: 4000/2000 MS (Java/Others)    Memory Limit: 262144/262144 K (Java/Others)
Total Submission(s): 2944    Accepted Submission(s): 1143

 

Problem Description

There are n apples on a tree, numbered from 1 to n.
Count the number of ways to pick at most m apples.

 

 

Input

The first line of the input contains an integer T (1≤T≤105) denoting the number of test cases.
Each test case consists of one line with two integers n,m (1≤m≤n≤105).

 

 

Output

For each test case, print an integer representing the number of ways modulo 109+7.

 

 

Sample Input

2 5 2 1000 500

 

 

Sample Output

16 924129523

 

[题意]  求  

[思路]

如果 直接求的话必然会超时.

所以这里用到了分块的思想

有 杨辉三角 和其前缀和

 

根据杨辉三角性质 C(n,m) = C(n-1,m) + C(n-1,m-1) 前缀和也有这个性质 

那么Sum(7,4) = 42+57 = 16+26+26+31

如果 我们以每5个为一组的话,  你会发现  Sum(7,4)  恰好 等于 C(2,0)*16 + C(2,1)*26 + C(2,2) * 31  = 99

7 和 5 差了 ,2   , 第7 项 可以有 第5 项推出来

这样的话, 我们推到1e+5  ,  1e5 分块的话 一块 333 差不多, 然后 我们只需要 处理 333,2*333,3*333,4*333.....

当  n <333  直接暴力就可以

当 n > 333 采用分块 找到最近的 那一块, 然后推出答案.

详细请看代码

 

[代码]

 

#include 
#include 
#define rep(i,a,n) for(int i = a ; i<=n;i++)
#define per(i,a,n) for(int i = n;i>=a;i--)

#define Si(x) scanf("%d",&x)

typedef long long ll;
const int maxn =1e5+10;
const int mod  =1e9+7;
using namespace std;
const int fk=332;
ll fac[maxn+5];
ll inv[maxn+5];
ll sum[350][maxn];
int n,m;

inline ll qpow(ll a,ll n)
{
    ll res = 1; for(;n;n>>=1){if(n&1)res =(res*a)%mod;a=a*a%mod;} return res;
}
void init()
{
    fac[0]=1;
    rep(i,1,maxn)
        fac[i] = (fac[i-1]*i)%mod;
    inv[maxn] = qpow(fac[maxn],mod-2);
    per(i,0,maxn-1)
        inv[i] =(inv[i+1]*(i+1))%mod;
}
ll C(ll n,ll m)
{
    if( m > n) return 0;
    if( m==n || m==0) return 1;
    return fac[n]*inv[n-m]%mod*inv[m]%mod;
}

void block()
{
    for(int i = fk; i< maxn; i+=fk)
    {
        ll res = 0;
        for(int j = 0 ; j =0 ;i--)
            {
                ans = (ans + C(p,cnt)*sum[d][i]) %mod;
                cnt --;
                if(cnt<0)
                    break;
            }
        }
        printf("%lld\n",ans%mod);
    }

    return 0;
}