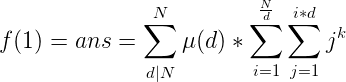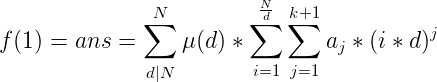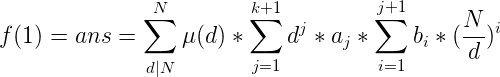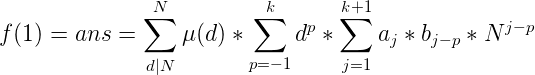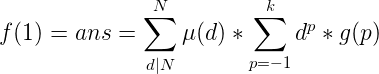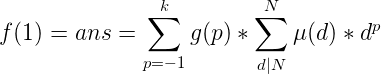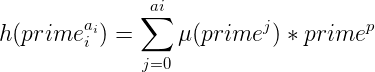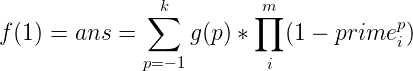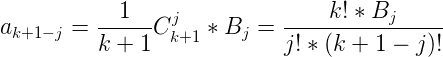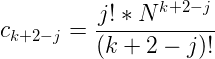HDU 6340 2018HDU多校赛 第四场 Delightful Formulas（莫比乌斯反演+伯努利数+NTT+积性）

 

 

 

大致题意：给你k和m，还有n分解质因子之后的质因子及其对应的指数，让你求 。

 

---

 

首先，这种含有gcd的式子，第一步肯定是进行莫比乌斯反演，这里由于前面好几篇都由类似的反演形式，所以我就不展开了，直接就得出反演之后的结果：

                                           

对于最右边的式子 ，我们把i*d看作定值，这就是关于i*d的一个k次幂和。对于这个k次幂和，我们可以用伯努利数进行展开。有公式：，即 一定是一个k阶多项式，那么可以改写成这样的形式，而这个多项式的系数可以证明与伯努利数有关。于是我们可以确定那么我们令，那么上面的式子可以写成：

                                          

交换一下求和次序：         

我们发现，这个最右边的东西如果把j看作是不变的，那么它还是一个幂和的形式，于是我们考虑再次用伯努利数对它进行展开。我们令 ，那么上面的式子可以写成：

                                         

接下来，用一个特别骚的替换操作，把式子简化。不妨设，那么p的取值范围是[-1,k]，那么原本的i就可以替换成 j-p，然后再交换求和次序整理一下，那么原式可以写成：

                                        

我们不妨令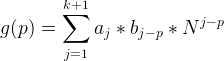，对于这个g(p)我们很高兴的发现，它是一个卷积的形式，因此我们可以用NTT在 的时间复杂度内预处理出 g(p) ，那么现在，原式就是这样的：

                                      

再次交换求和次序：     

注意到 是幂和的某一项，根据 dls 的论文，我们知道 是具有积性的。然后莫比乌斯函数 也是一个积性函数，因此这两个东西对应项相乘也是一个积性函数。于是可以用积性的性质去优化这个过程。不妨令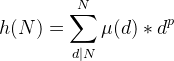，由于具有积性，所以，因此考虑每一个质因子即可。              

                                     

注意到，根据莫比乌斯函数的性质，当自变量是某一个质数的2次方及以上的时候，其函数值为0，那么只有当 j==1或2的时候式子才有意义。那么我们就可以很自然的写出  的通项：

                                      

那么最后的答案就是：

终于，我们推导完毕。我们发现，这个式子是O(KM)的，很愉快的可以解出这道题目。

 

---

 

最后呢，关于这个具体做法，还有一些细节对于第一次接触这种题的人来说需要交代一下。

                             

但我们的式子是 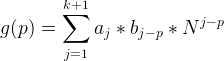，实际的卷积形式应该是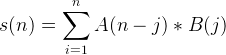，我们正好反过来了，因此实际用的时候要把下标统一，再反回去。首先的话把右边两项整理一下，变成 和 。后面哪一个只和p有关所以不用放到NTT中去求。然后是把下标换成 以及 。那么有：

                                        

                                        

然后你发现，当两个相乘的时候，一个是要除以 j! 一个是要乘以 j!，因此这两个可以抵消，所以我们又可以少几项。这样，我们枚举k+1-j和k+2-j，分别构造出a和c，然后这两个做一个NTT的卷积运算，最后每一项再乘以一个，就可以得到 。最后再积性搞搞即可。 

 

---

 

由于这个k可以到1e5这个级别，因此暴力的O(N^2)预处理伯努利数是不行的，因此还得加上一个多项式求逆。这个也是板子咯，反正还要用到NTT的卷积运算。具体见代码：

#include
#define file(x) freopen(#x".in","r",stdin),freopen(#x".out","w",stdout)
#define IO ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
#define mod 998244353
#define LL long long
#define N 550010
using namespace std;

int inv[N],fac[N],ifac[N],b[N],tmp[N];
int w,c[N],d[N],p[N],a[N],pw[N];

int qpow(int a,int b)
{
    int ans=1;
    while(b)
    {
        if(b&1)ans=(LL)ans*a%mod;
        a=(LL)a*a%mod; b>>=1;
    }
    return ans;
}

namespace NTT
{
    #define g 3
    int x[N<<2],y[N<<2],wn[N<<2];

    void init()
    {
        for(int i=0;i<21;i++)
        {
            int t=1<=k) j-=k,k>>=1;
            if(j>T;
    while(T--)
    {
        int k,w,n=1;
        cin>>k>>w;
        int len=1;
        while(len>p[i]>>a[i];
            n=n*(LL)qpow(p[i],a[i])%mod;
        }
        //cout<