激活函数:
传统神经网络中最常用的两个激活函数,Sigmoid系(Logistic-Sigmoid、Tanh-Sigmoid)被视为神经网络的核心所在.从数学上来看,非线性的Sigmoid函数对中央区的信号增益较大,对两侧区的信号增益小,在信号的特征空间映射上,有很好的效果,通过对加权的输入进行非线性组合产生非线性决策边界.从神经科学上来看,中央区酷似神经元的兴奋态,两侧区酷似神经元的抑制态,因而在神经网络学习方面,可以将重点特征推向中央区,将非重点特征推向两侧区.
Relu函数为现在深度学习使用比较广泛的激活函数,相比前面两个,其优点在于计算简单,导数简单,收敛快,单侧抑制 ,相对宽阔的兴奋边界 ,稀疏激活性;缺点在于在训练的时候,网络很脆弱,很容易出现很多神经元值为0,从而再也训练不动.一般将学习率设置为较小值来避免这种情况的发生.
比较:
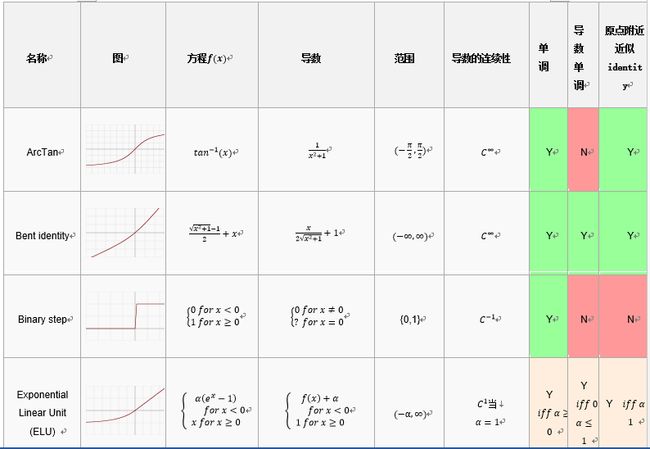
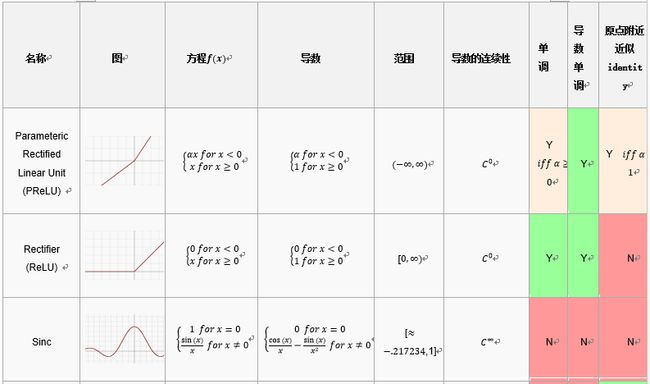
激活函数的一些可取的属性包括:
非线性:当激活函数是非线性的,然后一个两层神经网络可以证明是一个通用函数近似值.而identity激活函数不满足这个属性.当多层网络使用identity激活函数,整个网络就相当于一个单层模型.
连续可微的:这个属性对基于梯度优化方法是必要的.二进制激活函数在0点没有可微性,它在其他值上全部可导为0,基于梯度优化方法对于它毫无进展.
范围:当激活函数的范围是有限的,基于梯度的训练方法往往更稳定,因为模式显著影响几个有限权重.当范围是无限的,训练通常更有效率,因为模式显著影响大部分权重.在后一种情况下,较小的学习利率通常是必要的.
单调:当激活函数是单调时,与单层模型相关的错误表面是凸的.
平滑性:有单调导数的平滑函数已经被证明在某些情况下推广地更好.这些属性表明这些激活函数和Occam's razor更一致.
原点附近近似identity:当激活函数有这个属性,对于小的随机值初始化权重,神经网络将有效地学习.当激活函数没有这个属性,在初始化权值必须使用特殊例子.在下面的表中,激活函数,表明有该属性.
常见函数: