拼多多 2020校招 多多的电子字典（字典树前缀搜索，DP）

多多鸡打算造一本自己的电子字典，里面的所有单词都只由a和b组成。
每个单词的组成里a的数量不能超过N个且b的数量不能超过M个。
多多鸡的幸运数字是K，它打算把所有满足条件的单词里的字典序第K小的单词找出来，作为字典的封面。

解题思路：

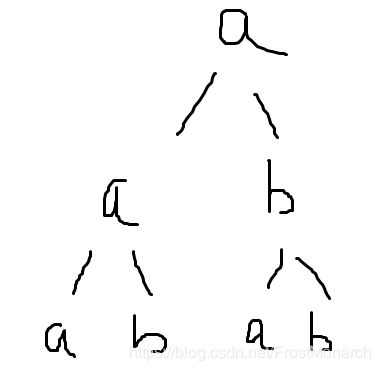
首先，答案最终的输出为上面这棵字典树的先序输出第k次。当然这棵树的a.b数量不能超过题目给的a,b数量。我们在先序输出的时候可以判断它的左子树的节点数是否小于k，是的话，我们左子树就可以不访问了。为此我们需要计算一个量dp[n][m][sta]；当sta == 0时，表示当前我们在'a'节点上，而且总共有n个a节点，m个b节点，注意包含自己。那么有如下转移公式：

    dp[n][m][sta]=1;
    if(!sta){
        dp[n][m][sta]+=((n>1)?dfs1(n-1,m,0):0) +((m>0)?dfs1(n-1,m,1):0);
    }else dp[n][m][sta]+=((n>0)?dfs1(n,m-1,0):0)+((m-1>0)?dfs1(n,m-1,1):0);

比较有疑惑的地方可能是为什么用了问号进行判断，因为我们的状态中要转移到下一个节点，必须保证那个节点还剩下。比如：我们不能转移到dp[n][m][sta]；其中假设 n==0,sta == 0； sta==0 代表这是一个1节点，所以n>=1。这是一个无效的状态

完整代码：

#include 
#define int unsigned long long 
using namespace std;
vector>> dp;
const int FLAG=1E18;
int  dfs1(int n,int m,int sta){
    if(n==0 && m==0)return dp[n][m][sta] = 0;
    if(dp[n][m][sta]!=FLAG)return dp[n][m][sta];
    if(sta == 2){ 
        dp[n][m][sta] = 0;
        dp[n][m][sta] = ((m>0)?dfs1(n,m,1):0);
        dp[n][m][sta]=  ((n>0)?dfs1(n,m,0):0);
        return dp[n][m][sta];
    }
    dp[n][m][sta]=1;
    if(!sta){
        dp[n][m][sta]+=((n>1)?dfs1(n-1,m,0):0) +((m>0)?dfs1(n-1,m,1):0);
    }else dp[n][m][sta]+=((n>0)?dfs1(n,m-1,0):0)+((m-1>0)?dfs1(n,m-1,1):0);
    return dp[n][m][sta];
}
string ans="";
void dfs2(int n,int m,int sta,int k,char t){
    ans+=t;
    k--;
    if(k==0)return;
    if(!sta){
        if(n>1 && dp[n-1][m][0]>=k)dfs2(n-1,m,sta,k,'a');
        else dfs2(n-1,m,!sta,k- ((n>1)?dp[n-1][m][sta]:0),'b');
    }else {
        if(n>=1 && dp[n][m-1][0]>=k)dfs2(n,m-1,!sta,k,'a');
        else dfs2(n,m-1,sta,k- ((n>=1)?dp[n][m-1][!sta]:0 ),'b');
    }
}
int32_t main(){
    int n,m,k;cin>>n>>m>>k;
    dp.assign(n+1,vector> (m+1,vector(3,FLAG)));
    dfs1(n,m,2);
    cerr<=k)dfs2(n,m,0,k,'a');
    else dfs2(n,m,1,k-dp[n][m][0],'b');
    cout<