数据结构——复习九(排序)

排序
稳定排序和不稳定排序
假设Ri=Rj(0<=i,j<=n-1,i≠j)，且在排序前的序列中Ri领先于Rj(即i 内部排序：待排序记录存放在内存
外部排序：排序过程中需对外存进行访问的排序
插入排序：直接插入排序、折半插入排序、希尔排序、表插入排序
交换排序：起泡排序、快速排序
选择排序：简单选择排序、堆排序
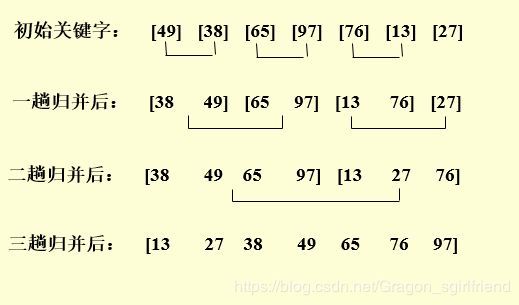
归并排序：2-路归并排序
分配排序
插入排序
直接插入排序

上面的过程很直观，挺简单的，对我来说比较好理解
//我自己写了一种，还有一种都是一样的，后面那种对理解shell排序比较有帮助

void straisort(int r[],int n)
{  int i,j,k;
   for(i=2;i<=n;i++)
   {  r[0]=r[i];
      j=i-1;
      for(k=1;k<=j;k++)
      {
          if(r[0]<r[k])
          r[k+1]=r[k];
          else
          {
          r[k+1]=r[0];
          break;
          }
      }
   }
} 

void straisort(int r[],int n)
{
    int i,j;
    for(i=2; i<=n; i++)
    {
        r[0]=r[i];
        j=i-1;
        while(r[0]<r[j])
        {
            r[j+1]=r[j];
            j--;
        }
        r[j+1]=r[0];
    }
}

时间效率：因为在最坏情况下，所有元素的比较次数总和为（0＋1＋…＋n-1)→O(n2)。其他情况下也要考虑移动元素的次数。 故时间复杂度为O(n2)
空间效率：仅占用1个缓冲单元——O(1)
算法的稳定性：因为a*排序后仍然在a的后面——稳定
二分法插入排序
这个跟上面那个画的流程是一样的，就是在查找插入地方的时候的方法，时间复杂度不同。

void binsort(int r[],int n)
{
    int i,l,x,s,m,k;
    for(i=2;i<=n;i++)
    {
        r[0]=r[i];
        x=r[i];
        s=1;
        l=i-1;
        while(s<=l)//通过二分查找s这个地方应该插入
        {
            m=(s+l)/2;
            if(x<r[m])  
            l=m-1;
            else 
            s=m+1;
        }
        for(k=i-1;k>=s;k--)
        r[k+1]=r[k];
        r[s]=r[0];
    }
}

时间复杂度：T(n)=O(n²) 移动次数没有减少
空间复杂度：S(n)=O(1)
shell排序
排序过程：先取一个正整数d1

void shellsort(int r[],int n,int d[],int T)
//数组d里存的是每一个逐渐缩小的d的值
{
    int i,j,k;
    int x;
    k=0;
    while(k<T)
    {
    for(i=d[k]+1;i<=n;i++)//先排距离为d的前两个，再慢慢增加
    {
     x=r[i];
     j=i-d[k];
     while((j>0)&&(x<r[j]))
     {
      r[j+d[k]]=r[j];
      j=j-d[k];
     }
     r[j+d[k]]=x;
    }
    k++;
    }
}

时间复杂度：T(n)=O(n1.3)
交换排序
冒泡排序

void  BubbleSort(int r[],int n)
{
    int flag=1；
    for(int i=1;i<=n-1&&flag;i++)
    {
     flag=0；
     for(j=1;j<=n-i;j++)//把第i大的放在第n-i+1个地方
     if(r[j]>r[j+1])
     {
      x= r[j];
      r[j]=r[j+1];
      r[j+1]= x;
      flag=1；
     }
     //如果在第2个for循环里没有进入，就说明不需要交换了，就跳出第一个，排好序了
    }
}

时间效率：O(n2) —因为要考虑最坏情况
空间效率：O(1) —只在交换时用到一个缓冲单元
稳 定 性：稳定 —a和a*在排序前后的次序未改变
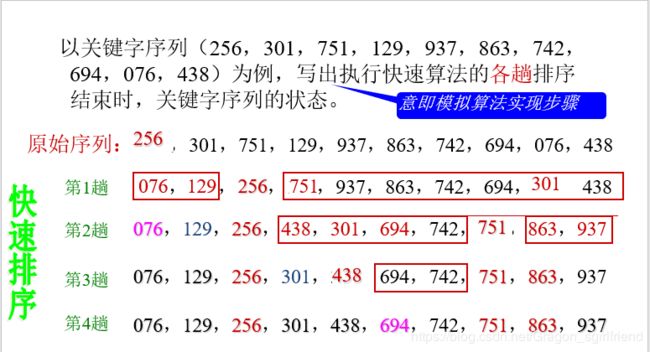
快速排序
基本思想：
用了递归，从待排序列中任取一个元素 （例如取第一个） 作为中心，所有比它小的元素一律前放，所有比它大的元素一律后放，形成左右两个子表。
然后再对各子表重新选择中心元素（例如取第一个）并依此规则调整，直到每个子表的元素只剩一个。此时便为有序序列了。

#include 
#include 
#include 
#include 
using namespace std;
int Partition(int r[],int low,int high)
{
    //一趟快排
    //交换子表 r[low…high]的记录，使支点（枢轴）记录到位，并返回其位置。
    //返回时，在支点之前的记录均不大于它，支点之后的记录均不小于它。
    //r[0]=r[low];//以子表的首记录作为支点记录，放入r[0]单元
    int pivotkey=r[low];//取支点的关键码存入pivotkey变量
    while(low<high)//从表的两端交替地向中间扫描
    {
        while(low<high&&r[high]>=pivotkey)
        high--;
        r[low]=r[high];//比支点小的记录交换到低端；
        while(low<high&&r[low]<=pivotkey)
        low++;
        r[high]=r[low];//比支点大的记录交换到高端；
    }
    r[low]=pivotkey;//支点记录到位；
    return low;//返回支点记录所在位置。
}
void QSort(int L[],int low,int high)
//对顺序表L中的子序列r[low…high]作快速排序
{
    if(low<high)
    {
     int pivot=Partition(L,low,high);
     QSort(L,low,pivot-1);
     QSort(L,pivot+1,high);
    }
}
int main()
{
    int a[100],n;
    scanf("%d",&n);
    for(int i=1;i<=n;i++)
    scanf("%d",&a[i]);
    QSort(a,1,n);
    for(int i=1;i<=n;i++)
    printf("%d ",a[i]);

    return 0;
}

时间效率：O(nlog2n)—因为每趟确定的元素呈指数增加
空间效率：O(log2n)—因为递归要用栈(存每层low，high和pivot)
稳定性：不稳定—因为有跳跃式交换
选择排序
直接选择排序

void smp_selesort(int r[],int n)
{
    int i,j,k;
    int x;
    for(i=1; i<n; i++)
    {
        k=i;
        for(j=i+1;j<=n;j++)
        if(r[j]<r[k])
        k=j;
        if(i!=k)
        {
            x=r[i];
            r[i]=r[k];
            r[k]=x;
        }
    }
}

时间效率：O(n2)
空间效率：O(1)
堆排序
将无序序列建成一个堆，得到关键字最小（或最大）的记录；输出堆顶的最小（大）值后，使剩余的n-1个元素重又建成一个堆，则可得到n个元素的次小值，重复执行，得到一个有序序列，这个过程叫堆排序。
我们要学会就是解决两个问题：
（1）如何由一个无序序列建成一个堆？
从无序序列的第【n/2】个元素（即此无序序列对应的完全二叉树的最后一个非终端结点）起，至第一个元素止，进行反复筛选

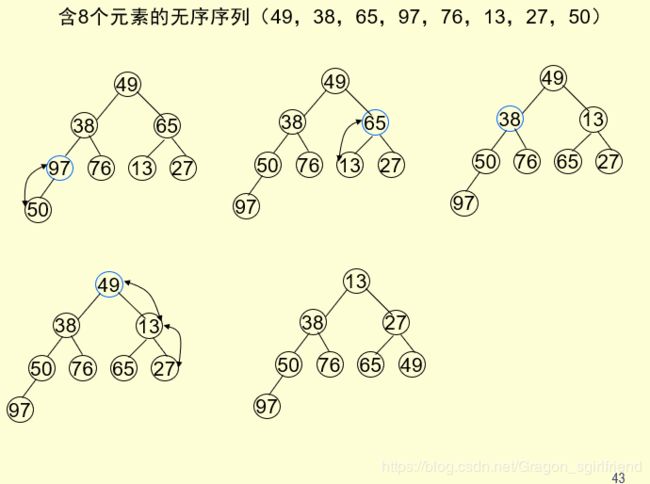
（2）如何在输出堆顶元素之后，调整剩余元素，使之成为一个新的堆？
输出堆顶元素之后，以堆中最后一个元素替代之；然后将根结点值与左、右子树的根结点值进行比较，并与其中小者进行交换；重复上述操作，直至叶子结点，将得到新的堆，称这个从堆顶至叶子的调整过程为“筛选”

int sift(int r[],int k,int m)
{
    int i,j;
    int x;
    i=k;
    x=r[i];
    j=2*i;
    while(j<=m)
    {
     if((j<m)&&(r[j]>r[j+1]))
     j++;
     if(x>r[j])
     {
      r[i]=r[j];
      i=j;
      j=j*2;
     }
     else   
     j=m+1;
    }
    r[i]=x;
}
/*sift作用：假设r[k+1..m]中各元素已经满足堆的定义，
sift使序列r[k..m]中的各元素满足堆的性质*/
void heapsort(int r[],int n)
{
  int i;
  int x;
  for(i=n/2;i>=1;i--)
  sift(r,i,n);
  for(i=n;i>=2;i--)
  {
   x=r[1];
   r[1]=r[i];
   r[i]=x;  //存放最小元素
   sift(r,1,i-1);
  }
}

时间复杂度：最坏情况下T(n)=O(nlog2n)
空间复杂度：S(n)=O(1)
稳定性：不稳定

归并排序

时间复杂度：T(n)=O(nlog2n)
空间复杂度：S(n)=O(n)
稳定